|
|
Скорости и ускорения различных точек вращающегося тела
тела, и линейными величинами щими движение точек тела. S , V , aτ, an и a , характеризую-
описываемому уравнением φ . Требуется определить ско- рость рого начального положения A0 , переместилась на расстояние
т. е. расстояние, пройденное точкой вращающегося тела, пропорцио- нально его углу поворота. Расстояние S и угол поворота φ – функции времени, a ρ – величина, постоянная для данной точки. Продиффе- ренцируем по времени обе части равенства (7.7) и получим
dt dφ = ωdt
– угловая скорость тела,
т. е. скорость точки вращающегося тела пропорциональна его угло- вой скорости.
Рис. 7.5. К определению скорости и ускорения точки
Из формулы (7.8) видно, что для точек, расположенных на оси
изменения ρ , т. е. у точек, находящихся дальше от оси вращения, скорости тем больше, чем больше значение ρ . Пропорциональная зависимость скоростей различных точек вращающегося тела от их расстояний относительно оси вращения показана на рис. 7.6.
Рис. 7.6. Распределение скоростей при вращательном движении твердого тела
Продифференцировав обе части равенства (7.8), имеем
dt dt
dω = εdt
– угловое ускорение тела, значит aτ
(7.9)
Подставив в формулу an (7.8), получим значение скорости из формулы
Из формулы a после подстановки вместо aτ и an их значений из формул (7.9) и (7.10) получаем
^
ется по одной из формул sin
a aτ , причем последнюю из них теперь можно представить в таком виде:
aτ ρε ε
(7.12)
Из формул (7.11) и (7.12) следует, что для точек тела при его вращательном движении по заданному закону можно сначала найти ускорение а, а затем разложить его на касательное ускорение aτи нормальное ускорение an, модуль которых
Способы передачи вращательного движения В технике часто возникает необходимость передачи вращатель- ного движения от одной машины к другой (например, от электро-
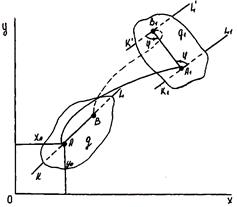
ГЛАВА 8. СЛОЖНОЕ ДВИЖЕНИЕ Сложное движение точки Примером сложного движения точки может служить: а) лодка (если ее принять за материальную точку), плывущая от одного берега реки к другому; б) шагающий по ступенькам движущегося эскалатора метро че- ловек, который также совершает сложное движение относительно неподвижного свода туннеля. Таким образом, при сложном движении точка, двигаясь относи- тельно некоторой подвижной материальной среды, которую усло- вимся называть подвижной системой отсчета, одновременно пе- редвигается вместе с этой системой отсчета относительно второй системы отсчета, условно принимаемой за неподвижную. Движение некоторой точки М по отношению к подвижной си- стеме отсчета называется относительным. Движение подвижной системы отсчета вместе со всеми связанными с ней точками мате- риальной среды по отношению к неподвижной системе отсчета для точки М называется переносным. Движение точки М по отношению к неподвижной системе отсчета называется сложным, или абсо- лютным. Для того чтобы видеть сложное (абсолютное) движение точки, наблюдатель сам должен быть связан с неподвижной системой от- счета. Если же наблюдатель находится в подвижной системе отсче- та, то он видит лишь относительную часть сложного движения. Представим, что точка М за некоторое время переместилась от- носительно подвижной системы координат O1X1Y1 из начального положения M0 в положение М1 по траектории M0М1 (траектории от- носительного движения точки) (рис. 8.1). За это же время Δt по- движная система координат O1X1Y1 вместе со всеми неизменно свя- занными с ней точками, а значит, и вместе с траекторией относи- тельного движения точки М переместилась в неподвижной системе координат OXY в новое положение:
Sабс
Рис. 8.1. К анализу сложного движения точки
, то получим
выражающее теорему сложения скоростей: при сложном движе- нии точки абсолютная скорость в каждый момент времени равна геометрической сумме переносной и относительной скоростей.
пер , отн ) , то модуль абсолютной скорости
образуется ромб (рис. 8.2, а) или равнобедренный треугольник (рис. 8.2, б) и, следовательно,
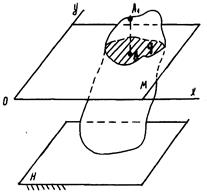
а б Рис. 8.2. Частный случай 8.2. Движение твердого тела, при котором все его точки движутся в плоскостях, параллельных некоторой неподвижной плоскости, называется плоскопараллельным (рис. 8.3).
Рис. 8.3. Плоскопараллельное движение твердого тела
Изучая плоскопараллельное движение тела М, достаточно рас- сматривать движение его плоского сечения q плоскости ХОY (рис. 8.4).
Рис. 8.4. К анализу плоскопараллельного движения твердого тела Выберем в сечении q произвольную точку A, которую назовем полюсом. С полюсом А свяжем некоторую прямую KL, а в самом сечении вдоль прямой KL проведем отрезок AB, перемещая плоское сечение из положения q в положение q1. Можно сначала передви- нуть его вместе с полюсом А поступательно, а затем повернуть на угол φ. Плоскопараллельное движение тела – движение сложное и со- стоит из поступательного движения вместе с полюсом и вращатель- ного движения вокруг полюса. Закон плоскопараллельного движения можно задать тремя урав- нениями:
Дифференцируя заданные уравнения плоскопараллельного дви-
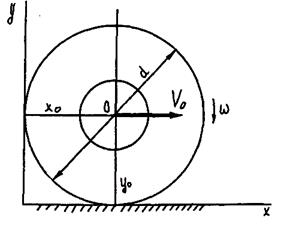
рение ε тела. полюса, а также угловую скорость ω и угловое уско- Пример 8.1.Пусть движение катящегося колеса диаметром d (рис. 8.5) задано уравнениями
где x0 и y0 – м, φ – рад, t – с. Продифференцировав эти уравнения, находим, что скорость по- люса O 0 dt угловая скорость колеса ω dφ
20 рад . с
Рис. 8.5. К примеру 8.1
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
Определим скорость и ускорение любой точки в любой момент времени. Для этой цели установим зависимость между угловыми величинами φ , ω и ε , характеризующими вращательное движение
Допустим, что тело, показанное на рис. 7.5, вращается по закону,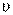
и ускорение a точки А этого тела, расположенной на рас- стоянии ρ от оси вращения O. Пусть тело за некоторое время t по- вернулось на угол φ, а точка А, двигаясь по окружности из некото-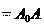
S . Так как угол φ выражается в радианах, то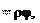
S (7.7)
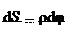dt dt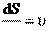
но – скорость точки, a
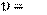ρω , (7.8)
вращения, ρ и скорости этих точек также равны нулю. По мере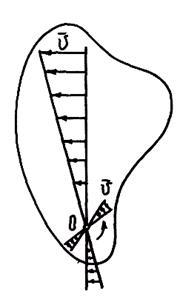
,
но – касательное ускорение точки, a
т. е. касательное ускорение точки вращающегося тела пропорцио- нально его угловому ускорению.
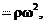an (7.10)
т. е. нормальное ускорение точки вращающегося тела пропорцио- нально второй степени его угловой скорости.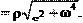
a (7.11)
Направление вектора ускорения, т. е. угол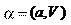
, определя-
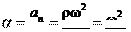tg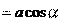
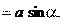aτ и an
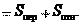
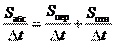и получим геометрическую сумму средних скоростей:
,
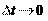которые направлены вдоль соответствующих векторов перемеще-
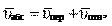
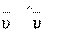Если задан угол (
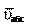Углы, образуемые векторами абсолютной скорости с век-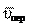
торами и , определяются по теореме синусов.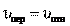
В частном случае при при сложении этих скоростей
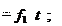
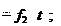
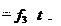x y φ
жения, можно в каждый момент времени определить скорость и
ускорение aA
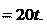x0 y0 φ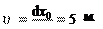
с dt