
|
|
Особенности расчета статически неопределимых стержневых системЕсли внутренние силы определялись только на основе условий равновесия отсеченной части системы (или отдельного бруса), си- стемы называют статически определимыми. Системы, в которых внутренние силовые факторы (ВСФ), в ча- стности продольные силы, не могут быть определены с помощью только метода сечений, называют статически неопределимыми системами. Соответственно задачи, связанные с расчетом указан- ных систем, также принято называть статически неопределимыми. Брус, изображенный на рис. 19.1, жестко заделан обоими конца- ми; в заделках возникают реакции, направленные вдоль оси бруса.
неизвестных же сил – две.
Рис. 19.1. Статически неопределимая система
Для решения статически неопределимой задачи помимо уравне- ний статики надо составить так называемые уравнения перемеще- ний, основанные на рассмотрении деформации системы (это гео- метрическая сторона задачи) и применении закона Гука. Пусть невесомая, весьма жесткая балка, нагруженная силой F, подвешена на стержнях (рис. 19.2). Стержни изготовлены из одина- кового материала и имеют одинаковые сечения. Система один раз статически неопределима: для плоской системы параллельных сил статика дает два независимых уравнения равновесия, а неизвестных сил – три. Обозначим реакции, так же, как и силы, действующие на стержни, через N1, N2, N3.
Рис. 19.2. Статически неопределимая задача Составляем уравнения равновесия приложенных к балке сил (рис. 19.3):
Рис. 19.3. Схема деформации системы
В результате деформации стержней балка займет положение, по- казанное на рис. 19.3 штриховыми линиями. Действительно, пред- положение о высокой жесткости балки позволяет пренебречь ее из- гибом, а симметрия самой системы и нагрузки приводит к заклю- чению, что все стержни удлиняются одинаково. Таким образом, геометрическая сторона задачи может быть выражена уравнением
Выражая удлинения стержней по формуле Гука, получим
откуда
19.3. Изгиб – это такой вид деформации бруса, при котором в его по- перечных сечениях возникают изгибающие моменты. В большин- стве случаев одновременно с изгибающими моментами возникают и поперечные силы; такой изгиб называют поперечным; если попе- речные силы не возникают, изгиб называют чистым. Плоскость, проходящую через продольную ось бруса (OZ) и од- ну из главных центральных осей его поперечного сечения (OY), называют главной плоскостью бруса(рис. 19.4).
Рис. 19.4. Схема нагружения бруса при прямом поперечном изгибе
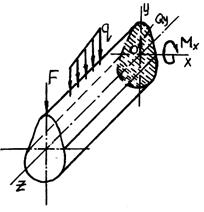
В случае если силовая плоскость, т. е. плоскость действия нагру- зок, совпадает с одной из главных плоскостей (см. рис. 19.4), имеет место прямой изгиб бруса. В общем случае прямого изгиба в попереч- ных сечениях бруса возникают два внутренних силовых фактора: по- перечная сила Qy и изгибающий момент Mx (рис. 19.5).
Рис. 19.5. Силовые факторы при изгибе
Границей между областями растяжения и сжатия является слой во- локон, который лишь искривляется, не испытывая при этом ни растя- жения, ни сжатия. Это так называемый нейтральный слой. Линия пе- ресечения нейтрального слоя с плоскостью поперечного сечения бруса называется нейтральной осью или нулевой линией (см. рис. 19.4). Брусья, работающие на прямой изгиб, принято называть балка- ми. Схемы основных типов статически определимых балок показа- ны на рис. 19.6: а – простая консоль; б – двухопорная балка без кон- солей; в – двухопорная балка с одной консолью; г – двухопорная балка с двумя консолями. Расстояние между опорами балки назы- вают пролетом, а длину балки, защемленной одним концом (рис. 19.9, а), иногда называют вылетом. Консолью называют часть балки, расположенную по одну сторону от опор (рис. 19.9, в, г).
Рис. 19.6. Обозначение балочных конструкций Учитывая, что при прямом поперечном изгибе все внешние силы расположены в одной плоскости, при определении ВСФ нет на- добности прибегать к аксонометрическим изображениям. Брус (балку) изображают одной линией, к которой приложены за- данные нагрузки. Эта линия представляет собой продольную ось бруса. Рассмотрим двухопорную балку (рис. 9.7). Считаем, что опорные реакции известны.
Рис. 19.7. К определению внутренних силовых факторов в сечении изгибаемой балки
Определяем реакции в опорах:
откуда Qy RA
qz;
откуда z
Изгибающий момент Mxв произвольном поперечном сечении бруса численно равен алгебраической сумме моментов всех внешних сил, приложенных к отсеченной части, относительно той точки продольной оси бруса, через которую проходит рассматриваемое сечение. Для определенности при построении эпюр поперечных сил и из- гибающих моментов установим для них правила знаков. При построении эпюр удобнее устанавливать знаки Qyи Mxпо внешним силам. Внешняя сила, стремящаяся повернуть отсеченную часть балки по часовой стрелке вокруг той точки оси, которая соответствует проведенному сечению, вызывает положительную поперечную силу (рис. 19.8, а). Внешняя сила (момент), изгибающая эту часть выпуклостью вниз, т. е. таким образом, что сжатые волокна находятся сверху, да- ет положительный изгибающий момент (рис. 19.8, б).
Рис. 19.8. Правило знаков для Qyи Mx 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Таким образом на брус действует система сил, направленных по од- ной прямой; статика в этом случае дает одно уравнение равновесия:
Таким образом на брус действует система сил, направленных по од- ной прямой; статика в этом случае дает одно уравнение равновесия: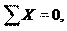


 (19.1)
(19.1)
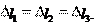
 ,
, N1 . (19.2)
N1 . (19.2)





 Mk 0; RAz qz 2 Mx 0,
Mk 0; RAz qz 2 Mx 0, Mx .
Mx .