
|
|
Определение скорости точкипри естественном способе задания ее движения Пусть движение точки А по заданной траектории происходит со-
момент времени t (рис. 6.8).
Рис. 6.8. Дуговая координата движения точки:
t t положение точки А1; За время точка
За промежуток времени t проходит путь L S S1 S.
значение средней скорости на этом пути
но оно отличается от значения скорости в момент времени t. Ско- рость в заданный момент t
т. е. значение скорости точки, движение которой задано естествен- ным способом, в любой момент времени равно первой производной от расстояния (дуговой координаты) по времени. Направление скорости, как отмечалось выше, известно заранее.
Определение ускорения точки при естественном способе задания ее движения
ускорений:
Рис. 6.9. Нормальное (а) и касательное (б) ускорения точки
dt
(t) ,
равный производной от скорости в данный момент по времени или, иначе, второй производной от расстояния по времени, характеризу- ет быстроту изменения значения скорости.
в любой момент времени перпендикуля-
Значит, модуль нормального ускорения пропорционален второй степени модуля скорости в данный момент, обратно пропорциона- лен радиусу кривизны траектории в данной точке и характеризует быстроту изменения направления скорости. Модуль ускорения
рических функций по одной из следующих формул:
cos
tg at
или ). Если
Частные случаи движения точки 1. , то точка движется
прямолинейно, так как при an неизменным. направление скорости остается 2. равномерного движения 0, const уравнение
При начальном расстоянии S0 , т. е. точка в момент начала
0 и an 0 , то движение точки называется равномер-
0 и an , то точка движется рав-
Равномерное движение точки по окружности
0 и an
окружности ρ . Из формулы S S0 t скорость рав-
Рис. 6.10. Равномерное движение точки по окружности
Если принять t = Т – периоду, т. е. времени одного обхода точ-
T T
3. Равнопеременное движение. Если a d const , то дви-
жение точки называется равнопеременным. Уравнение равнопеременного движения точки
– скорость в любой момент времени.
А. При равнопеременном прямолинейном движении, если не из- вестно время t, получим первую вспомогательную формулу
S ,
движении. – средняя скорость точки при ее равномерном
отсчета траектории (S0 = 0) и без начальной скорости ( предыдущие формулы приобретают более простой вид: ), то
S ;
В. При свободном падении A a g 9,81 м с2 . В этом слу-
gt 2
H
Предпоследняя из этих формул, представленная в виде
ГЛАВА 7. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА Поступательное движение Движение твердого тела, при котором любой выбранный в теле отрезок прямой перемещается, оставаясь параллельным своему пер- воначальному положению, называется поступательным. Рассмотрим две точки А и В, соединенные отрезком АВ (рис. 7.1). Очевидно, что при перемещении отрезка АВ параллельно первоначальному положению ( AB || A1B1 || A2 B2 ) точки A и В дви- жутся по одинаковым траекториям, т. е. если траекторию BB1B2 совместить с траекторией AA1 A2 , то они совпадут. Если вместе с
CC1C2 ) одинакова с траекториями AA1 A2 и BB1B2 :
Рис. 7.1. К анализу поступательного движения твердого тела
Как видим, поступательное движение твердого тела полностью харак- теризуется движением любой его точки. Обычно поступательное движе- ние тела задается движением его центра тяжести, иначе говоря, при по- ступательном движении тело можно считать материальной точкой. Примерами поступательного движения тел могут служить какой- либо ползун 1, движущийся в прямолинейных направляющих 2 (рис. 7.2, а), или прямолинейно движущийся автомобиль (вернее, не
Примерами криволинейного поступательного движения служат движение вагончика (люльки) подвесной канатной дороги (рис. 7.2, б) или движение спарника (рис. 7.2, в), соединяющего два параллельных кривошипа. В последнем случае каждая точка спар- ника движется по окружности.
Рис. 7.2. Примеры поступательного движения тел:
7.2. Движение твердого тела, при котором все его точки перемеща- ются по окружности, центры которой расположены на перпендику- лярной этим окружностям неподвижной прямой, называется вра- щательным. Неподвижная прямая, на которой лежат центры кру- говых траекторий точек тела, называется его осью вращения. Для образования оси вращения достаточно закрепить какие-либо две точки тела. В качестве примеров вращательного движения тел мож- но привести движение дверей или створок окон при их открывании или закрывании. Представим себе тело в виде цилиндра, ось AB которого лежит в подшипниках (рис. 7.3).
Рис. 7.3. К анализу вращательного движения твердого тела
Движением одной какой-либо точки однозначно определить вращательное движение тела нельзя. Для установления закона вращательного движения тела, по кото- рому можно определять его положение в данный момент, проведем через ось вращения тела связанную только с нею неподвижную по- луплоскость НП, а внутри тела отметим подвижную полуплоскость, которая вращается около оси вместе с телом, теперь угол φ, образу- емый в каждый данный момент времени полуплоскостями НП и ПП, точно определяет положение тела в пространстве (см. рис. 7.3). Угол φ называется углом поворота и выражается в радианах. Чтобы определять положение тела в пространстве в любой момент време- ни, необходимо знать зависимость между углом поворота φ и вре- менем t, т. е. знать закон вращательного движения тела:
Представим, что в некоторый момент времени t положение вра- щающегося тела определяется углом поворота φ, а в момент t + Δt – углом поворота φ + Δ φ. Следовательно, за время Δt тело поверну- лось на угол Δ φ, и величина
называется средней угловой скоростью.
Единицей угловой скорости является 1 рад/с. Характеристикой быстроты изменения угловой скорости служит угловое ускорение,
Единица углового ускорения 1 рад/с2.
Условимся угол поворота, отсчитываемый против хода часовой стрелки, считать положительным, а отсчитываемый по ходу часо- вой стрелки – отрицательным. Рис. 7.4. К определению вида вращательного движения

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
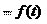 гласно уравнению S , требуется определить скорость точки в
гласно уравнению S , требуется определить скорость точки в
 t положение точки А;
t положение точки А;

 точка прошла путь L ,
точка прошла путь L , ,
, ,
, Вектор a – ускорение точки в данный момент (рис. 6.9, а) – есть
Вектор a – ускорение точки в данный момент (рис. 6.9, а) – есть
 геометрическая сумма касательного a и нормального an
геометрическая сумма касательного a и нормального an
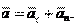

 Вектор a в любой момент времени направлен по касательной (рис. 6.9, б), поэтому вектор a называется касательным, или тан- генциальным ускорением. Модуль касательного ускорения
Вектор a в любой момент времени направлен по касательной (рис. 6.9, б), поэтому вектор a называется касательным, или тан- генциальным ускорением. Модуль касательного ускорения a d f
a d f Доказано, что вектор an
Доказано, что вектор an an .
an .
 a ,
a , а направление a (угол ) находим с помощью тригономет-
а направление a (угол ) находим с помощью тригономет- sin
sin a
a a
a

 Если векторы
Если векторы  a имеют одинаковые знаки (
a имеют одинаковые знаки (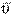 же векторы
же векторы 
 a разные ( или ).
a разные ( или ).
 Прямолинейное движение. Если an
Прямолинейное движение. Если an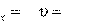 Равномерное движение.При a
Равномерное движение.При a S .
S .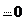

 Если a
Если a
 номерно по криволинейной траектории.
номерно по криволинейной траектории. , так
, так
 как при равномерном движении const , а при движении по
как при равномерном движении const , а при движении по .
.
 кой окружности, то S и
кой окружности, то S и
 или ,
или ,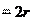 где d – диаметр окружности.
где d – диаметр окружности. dt
dt S .
S .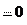 an и a
an и a
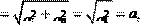 .
. S
S
 Если не известно a :
Если не известно a : где
где Б. Если равноускоренное движение точки начинается из начала
Б. Если равноускоренное движение точки начинается из начала
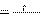 a t2
a t2 S
S Примерами такого движения могут служить движение автомоби- ля при трогании с места или движение самолета на взлетной полосе, а также известное из физики свободное падение тел.
Примерами такого движения могут служить движение автомоби- ля при трогании с места или движение самолета на взлетной полосе, а также известное из физики свободное падение тел.
 H ;
H ; 2
2 H t.
H t. , называется формулой Галилея.
, называется формулой Галилея.

 , или , или ;
, или , или ;

 aA , или aA1 , или aA2 .
aA , или aA1 , или aA2 .

 а – прямолинейного; б, в – криволинейного
а – прямолинейного; б, в – криволинейного
 φ
φ ωср
ωср ω
ω обозначаемое ε . Среднее ускорение εср ;
обозначаемое ε . Среднее ускорение εср ; ε .
ε .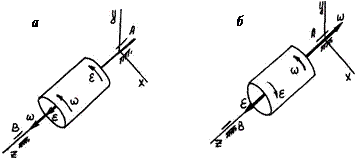


 Векторы ω и ε – это скользящие векторы, которые направлены по оси вращения, чтобы, глядя из конца вектора ω (или ε ), видеть вращение, происходящее против часовой стрелки.
Векторы ω и ε – это скользящие векторы, которые направлены по оси вращения, чтобы, глядя из конца вектора ω (или ε ), видеть вращение, происходящее против часовой стрелки.
 Если векторы ω и ε направлены в одну сторону (рис. 7.4, а), то
Если векторы ω и ε направлены в одну сторону (рис. 7.4, а), то