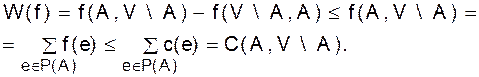|
|
Максимальный поток в сетиПод сетью будем понимать пару S=<G, c >, где G = <V, E> - произвольный ориентированный граф, а с: Если для
определяет «количество потока», выходящего из вершины v. Если Df(v) > 0, то вершина v называется источником, если Df(v) < 0, то вершина v называется стоком. Для большинства вершин Df(v)>0. Выделим в нашей сети две вершины - источник s и сток t. Под потоком из вершины s в вершину t в сети S будем понимать произвольную функцию 1. 2. Величину Такой поток может описывать, например, поведение газа или жидкости в трубопроводе, потоки автомобилей, движение по железной дороге, передачу информации в информационной сети. Мы будем интересоваться нахождением максимального потока в сети. Под разрезом Р(А)сети S, соответствующим подмножеству
Разрез - это линия или множество линий, которые полностью разделяют источник и сток. Для произвольного потока f в сети S поток через разрез Р(А) определяется естественным образом:
Лемма 3.24.Если W(f)=f(A,V\A) - f(V\A,A) В общем виде лемма говорит, что общее количество потока можно измерить в произвольном разрезе, отделяющем s от t. В частности, если A=V\{t},получаем в этом случае из леммы:
что выражает интуитивно понятный факт: в сток входит в точности такое количество потока, какое выходит из источника. Доказательство леммы. Просуммируем уравнения Каждое из слагаемых Определим пропускную способность разреза Р(А) следующим способом:
Под минимальным разрезом, разделяющим s и t, будем понимать произвольный разрез Р(А), Теорема 3.25. Величина каждого потока из sв t не превосходит пропускной способности минимального разреза, разделяющего s и t, причем существует поток, достигающий этого значения. Доказательство. Пусть Р(А) - минимальный разрез. В силу леммы для произвольного потока f имеем
Существование потока, для которого указанное неравенство переходит в равенство (такой поток, очевидно, максимален), гораздо более глубокий факт, который здесь мы доказывать не будем. ð Рекомендуемая литература. 1. Стенли Р. Перечислительная комбинаторика. -М.: Мир, 1990. 2. Липский В. Комбинаторика для программистов. - М.: Мир, 1988. 3. Рыбников К.А. Введение в комбинаторный анализ. - М.: МГУ,1985. 4. Гаврилов Г.И., Сапоженко А.А. Задачи и упражнения по курсу дискретной математики. -М.: Наука, 1992. 5. Риордан Дж. Введение в комбинаторный анализ. - М.: ИЛ, 1963. 6. Холл М. Комбинаторика. - М.: Мир, 1970. 7. Мендельсон Э. Введение в математическую логику.- М.: Наука, 1976. 8. Дискретная математика и математические вопросы кибернетики/ Под ред. С.В.Яблонского, О.В.Лупанова, Т.1, -М.; Наука, 1974. 9. Яблонский С.В. Введение в дискретную математику. -М.: Наука, 1979. 10. Оре О. Теория графов. - М.: Наука, 1968. 11. Кристофидис Н. Теория графов. Алгоритмический подход. -М.: Мир, 1987. 12. Емеличев В.А., Мельников О.И. и др. Лекции по теории графов. М.: Наука, 1990. 13. Уилсон Р.Дж. Введение в теорию графов. - М.: Мир, 1977. 14. Харари Ф. Теория графов. - М.: Мир,1973.
Оглавление 1. Элементы комбинаторики.......................................................... 3 1.1. Введение................................................................................... 3 1.2. Два принципа комбинаторики................................................ 4 1.3. Функции и размещения........................................................... 4 1.3.1. Числа Стирлинга первого рода....................................... 7 1.3.2. Циклическая структура перестановок............................. 8 1.3.3. Упорядоченные размещения.......................................... 10 1.3.4. Сочетания и биномиальные коэффициенты................. 13 1.3.5. Полиномиальные коэффициенты................................... 26 1.4. Разбиения............................................................................... 29 1.4.1. Число разбиений............................................................. 29 1.4.2. Числа Белла..................................................................... 33 1.5. Принцип включений - исключений....................................... 33 1.5.1. Задача о числе беспорядков (Задача о встречах)......... 38 1.5.2. Количество сюръективных отображений...................... 41 1.5.3. Перестановки с ограничениями на местоположение... 42 1.6. Системы представителей множеств...................................... 47 1.6.1. Системы различных представителей............................. 47 1.6.2. Системы общих представителей.................................... 52 2. Функции алгебры логики............................................................. 54 2.1. Элементарные высказывания................................................ 56 2.2. Элементарные логические операции (функции).................. 58 2.3. Алгебраические свойства элементарных операций............. 63 2.4. Разложение функций алгебры логики по переменным........ 66 2.5. Функциональная полнота систем функций алгебры логики 71 2.5.1. Замкнутые классы........................................................... 73 2.5.2. Критерий полноты.......................................................... 82 2.5.3. Представление о результатах Поста.............................. 89 3. Элементы теории графов............................................................. 91 3.1. Степени вершин..................................................................... 93 3.2. О машинном представлении графов.................................... 94 3.3. Поиск в графе........................................................................ 97 3.3.1. Поиск в глубину в графе................................................ 97 3.3.2. Поиск в ширину в графе.............................................. 100 3.4. Пути и циклы....................................................................... 102 3.5. Связность............................................................................. 103 3.6. Деревья................................................................................ 105 3.6.1. Остовное дерево (каркас)............................................. 110 3.7. Эйлеровы пути и циклы...................................................... 114 3.7.1. Aлгоритм построения эйлерова цикла........................ 116 3.8. Гамильтоновы пути и циклы............................................... 119 3.9. Нахождение кратчайших путей в графе............................. 128 3.9.1. Алгоритм нахождения расстояния от источника до всех остальных вершин в ориентированном графе с неотрицательными весами ребер........................................ 129 3.10. Максимальный поток в сети.............................................. 131 Рекомендуемая литература........................................................ 134

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 - функция, которая каждому ребру <u,v> ставит в соответствие неотрицательное вещественное число с(u,v), называемое пропускной способностью ребра.
- функция, которая каждому ребру <u,v> ставит в соответствие неотрицательное вещественное число с(u,v), называемое пропускной способностью ребра. f(u,v) мы интерпретируем как поток из u в v , то величина
f(u,v) мы интерпретируем как поток из u в v , то величина  ,
, ,
,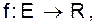 для которой выполняются условия:
для которой выполняются условия: для всех ребер <u, v> Î E;
для всех ребер <u, v> Î E;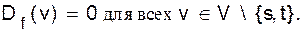
 будем называть величиной потока.
будем называть величиной потока.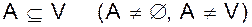 мы понимаем множество ребер <u,v>ÎE, таких, что
мы понимаем множество ребер <u,v>ÎE, таких, что  т.е.
т.е.  .
.
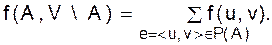
 и
и  то для произвольного потока f из sв tимеет место соотношение
то для произвольного потока f из sв tимеет место соотношение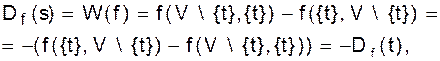
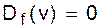 для всех
для всех  Эта сумма состоит из некоторого количества слагаемых
Эта сумма состоит из некоторого количества слагаемых  со знаком + или - , причем хотя бы одна из вершин принадлежит А. Если обе вершины принадлежат А, то
со знаком + или - , причем хотя бы одна из вершин принадлежит А. Если обе вершины принадлежат А, то  и со знаком минус в
и со знаком минус в  , что в сумме дает 0.
, что в сумме дает 0. появляется в точности один раз со знаком плюс в
появляется в точности один раз со знаком плюс в  , отвечают за слагаемое
, отвечают за слагаемое  С другой стороны, сумма равна
С другой стороны, сумма равна 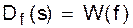 , ибо
, ибо 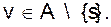
 .
. , с минимальной пропускной способностью. Фундаментальным фактом теории потоков в сетях является классическая теорема о максимальном потоке и минимальном разрезе.
, с минимальной пропускной способностью. Фундаментальным фактом теории потоков в сетях является классическая теорема о максимальном потоке и минимальном разрезе.