
|
|
Сочетания и биномиальные коэффициенты.Простейшими комбинаторными объектами являются сочетания и биномиальные коэффициенты. Пусть дано конечное множество X , содержащее n различных элементов. Нас интересует количество различных k- элементных подмножеств, которые можно образовать из элементов множества X. Два подмножества считаются различными, если они различаются хотя бы одним входящим в них элементом. Такие подмножества называются сочетаниями из m элементов по k элементов и обозначаются Утверждение 1.8. Число различных подмножеств из k элементов множества A, |A |= m есть
Первое доказательство. Построим таблицу T всех строго возрастающих (монотонных, без повторений букв) слов длины k в алфавите A из m букв. Пример. Пусть множество A состоит из пяти различных элементов: A= {a,b,c,d,c} . Положим k=3. Тогда таблица T всех строго возрастающих слов длины 3 в алфавите A имеет следующий вид: abc acd adc abd ace abe bcd bde bce cde ð Переставим буквы в каждом слове всеми возможными способами и обозначим получившуюся таблицу T¢. T¢ - множество слов без повторения букв длины k в алфавите A. В таблице T¢ нет пропусков: каждое слово длины k появится в таблице T¢. В таблице T¢ нет повторений: два слова из T¢ либо получены из одного слова T и тогда отличаются порядком букв, либо из разных слов T и тогда различаются буквами. По утверждению1.2: | T¢ | = [ m ]k. Поэтому | T | = [ m ]k / k! . Таким образом, окончательно получаем
Второе доказательство. Определим множество
С другой стороны, можно взять n способами любой элемент множества S в качестве первого, n-1 способом любой из оставшихся элементов в качестве второго и так далее, k-ый элемент можно выбрать из оставшихся n - k + 1 способом. Следовательно, N(n, k) = n(n - 1) ... (n - k + 1). Итак, мы дали комбинаторное доказательство того, что
и, следовательно,
Прежде, чем двигаться дальше сделаем небольшое отступление, связанное с введением понятия производящих функций. Производящие функции Производящие функции неизменно и естественно появляются во всех разделах перечислительного комбинаторного анализа. Мы будем делать акцент на наиболее органичном применении производящих функций для получения и проверки комбинаторных тождеств, когда другие методы менее естественны или менее эффективны. Производящие функции часто применяются в качестве метода, альтернативного методу рекуррентных соотношений, в частности с их помощью выводятся взаимно обратные соотношения. Путь задана последовательность а1, а2, ... , аn, ... (неважно, конечная или бесконечная). Производящей функцией последовательности а1, а2, ... , аn, ... называется функция Например, из формулы
вытекает, что функция Возводя обе части последнего разложения в квадрат, получаем
откуда следует, что для последовательности 1, 2, 3, ... , n, ... производящей функцией является функция Нас будут интересовать производящие функции для последовательностей a0, a1, ... , an, ..., так или иначе связанных с комбинаторными задачами. С помощью производящих функций удается получать и исследовать самые разные свойства этих последовательностей. Пусть
имеем
или в общем виде
В таком случае говорят, что последовательность коэффициентов cnесть свертка (произведение Коши) последовательностей anи bn. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , а их количество
, а их количество  обозначается
обозначается  или
или  . Обозначение читается как “число сочетаний из m по k “ или просто “из m по k”.
. Обозначение читается как “число сочетаний из m по k “ или просто “из m по k”.

 (иногда обозначаемое как-нибудь иначе) как множество всех k-элементных подмножеств (или k-подмножеств) множества S и положим по определению
(иногда обозначаемое как-нибудь иначе) как множество всех k-элементных подмножеств (или k-подмножеств) множества S и положим по определению 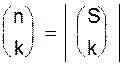 (игнорируя прошлое использование символа
(игнорируя прошлое использование символа 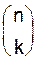 ). Подсчитаем двумя способами число N(n, k) способов, которыми можно выбрать k-подможество T множества S, а затем линейно упорядочить его элементы. Множество T мы можем выбрать
). Подсчитаем двумя способами число N(n, k) способов, которыми можно выбрать k-подможество T множества S, а затем линейно упорядочить его элементы. Множество T мы можем выбрать  .
. ,
, . ð
. ð . При этом все рассматриваемые ряды в случае бесконечной последовательности считаются формально сходящимися (если эти ряды сходятся в какой-то области к функции f(x)), поскольку мы интересуемся не областью сходимости соответствующих рядов, а лишь соотношениями между коэффициентами таких рядов.
. При этом все рассматриваемые ряды в случае бесконечной последовательности считаются формально сходящимися (если эти ряды сходятся в какой-то области к функции f(x)), поскольку мы интересуемся не областью сходимости соответствующих рядов, а лишь соотношениями между коэффициентами таких рядов.
 является производящей функцией для последовательности чисел 1, 1, 1, ... , 1, ...
является производящей функцией для последовательности чисел 1, 1, 1, ... , 1, ... ,
, .
. - производящая функция последовательности b1, b2, ... , bn, ... и
- производящая функция последовательности b1, b2, ... , bn, ... и  - производящая функция последовательности c1, c2, ... , cn, ... . Тогда из равенства
- производящая функция последовательности c1, c2, ... , cn, ... . Тогда из равенства

 .
.