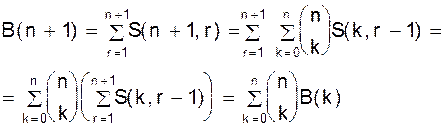|
|
Полиномиальные коэффициентыУтверждение 1.9. Пусть X множество n различных объектов и пусть n1, n2,..., np неотрицательные целые числа, удовлетворяющие условию n1+ n2 + ... +np = n; количество размещений n объектов по ячейкам Y1,...,Yp, при которых каждая ячейка содержит n1, n2, ..., npобъектов соответственно, есть
Доказательство. Пусть n1+ n2+ ...+ np= n. Ящик Y1 можно наполнить Следовательно, искомое число размещений равно
ð Утверждение 1.10. Производящая функция для полиномиальных коэффициентов имеет следующий вид:
Доказательство. Для доказательства справедливости равенства (1.10) достаточно заметить, что коэффициент при Следствие 1.
Для доказательства следствия 1 достаточно заметить, что
Отсюда следует равенство коэффициентов при соответствующих степенях в левой и правой частях последнего равенства:
Следствие 2.
Указанное равенство есть непосредственное следствие следующего соотношения для производящих функций:
Следствие 3.
Равенство следствия 3 непосредственно вытекает из вида производящей функции для полиномиальных коэффициентов, если в (1.10) положить: x1= x3= x5= ... = +1 , x2 =x4= x6= ... = –1 . ð Разбиения Число разбиений Определение. Разбиение конечного множества X, êX ê= n , есть неупорядоченный набор p = {B1 , B2, ... , Bk } подмножеств множества X таких, что Bi ¹ Æ для всех i от 1 до k; Bi Ç Bj = Æ , если i ¹ j B1 È B2 È ... ÈBk = X. Мы называем Biклассом (блоком) разбиения p и говорим, что p имеет k классов. Пусть S(n, k) - число разбиений n - множества на k классов. S(n, k) называется также числом Стирлинга второго рода.ð Разбиения соответствуют размещениям n различных объектов по k одинаковым ящикам при условии, что каждый ящик не пуст. Пример. S (4, 2) =7. Действительно, четыре объекта {1, 2, 3, 4} можно следующим образом разбить на два класса: {1}Ç{2, 3, 4}; {3}Ç{1, 2, 4}; {1, 2}Ç{3, 4}; {2}Ç{1, 3, 4}; {4}Ç{1, 2, 3} {1, 3}Ç{2, 4}; {1, 4}È{2, 3}. ð Условимся полагать, что S(0,0) = 1. Читатель должен убедиться, что для n ³ 1 имеют место соотношения: S(0, k) = 0 при k>0, S(n, k) = 0 при k > n, S(n, 0) = 0, S(n, 1) = 1, S(n,2) = 2n-1 - 1, S(n, n) =1, S(n, n - 1) = Утверждение 1.11. Числа Cтирлинга второго рода удовлетворяют следующему основному рекуррентному соотношению: S(n+1, k) = S(n, k - 1) + kS(n, k). (1.12) Доказательство. Рассмотрим таблицу разбиений n+1 объекта на k классов. 1) Для некоторых разбиений (n+1)-ый объект есть единственный элемент в классе. Число таких разбиений есть S(n, k - 1). 2) Для других разбиений (n+1)-ый объект не является единственным элементом класса ни для какого класса. Следовательно, существует kS(n, k) таких разбиений, так как каждому разбиению множества {1, ... , n} на k классов соответствует в точности k разбиений, образованных добавлением элемента n+1 поочередно к каждому классу. Таким образом, мы представили все разбиения n+1 элемента на k классов в виде объединения непересекающихся подмножеств разбиений двух перечисленных типов. Поэтому S(n+1, k) = S(n, k - 1) + kS(n, k). Утверждение 1.12. Число сюръективных отображений множества X, |X| = n, на множество Y (|Y| = m) равно m!S(n, m). Доказательство. Каждое сюръективное отображение X = {1,2,...,n} на Y = {y1,y2,...,ym} индуцирует разбиение X на m различных классов 1,2,..., m (в класс i попадают все такие x, что f(x) = yi); наоборот, каждому разбиению X на m классов соответствует m! сюръективных отображений X на Y. Действительно, выражение m!S(n, m) дает число способов разбить X на m классов, а затем линейно упорядочить классы, скажем, (B1 , B2 , ... , Bm ). Свяжем последовательность Ниже приводится список некоторых основных формул для количества разбиений множества из n элементов на k классов - S(n,k). Формула 1.
Числа S(n, k) играют обратную роль по отношению к числам s(n, k) - позволяют перейти от базиса 1, x, x2,... к базису Доказательство. Рассмотрим всевозможные отображения множества X из n элементов ( |X| = n) во множество Y из m элементов (|Y| = m). С одной стороны, по утверждению 1.1 количество таких отображений есть mn . С другой стороны, каждое такое отображение есть сюръективное отображение множества X на подмножество BÍY. Для произвольного подмножества B
Равенство (1.14) можно рассматривать как равенство двух многочленов переменной x при всех целых положительных значениях x = m. Следовательно, эти многочлены тождественно равны между собой, так как их разность может быть либо тождественным нулем, либо должна иметь бесконечное число нулей, что невозможно. Справедливость формулы (1.13) доказана. ð Формула 2.
Доказательство. Рассмотрим множество всех разбиений множества X={1, 2, ..., n+1} на m классов. Количество таких разбиений есть S(n+1, m). Все разбиения распадаются на различные типы, соответствующие разным подмножествам множества X, содержащим элемент n+1. Для каждого k- элементного подмножества B Ì X, содержащего элемент n+1, существует в точности S(n+1- k, m-1) разбиений множества X на m-1 класс, содержащих B в качестве класса. Действительно, каждое такое разбиение однозначно соответствует разбиению множества X \ B на m-1 класс. k - элементное подмножество B Ì X, содержащее элемент n+1 можно выбрать
3.Вернемся еще раз к связи комбинаторных объектов с исчислением конечных разностей. Из формулы (1.13) следует, что, например,
откуда заключаем на основании разложения (1.8): 1! S(4, 1) = 1, 2! S(4, 2)=14, 3! S(4, 3) = 36, 4! S(4, 4) = 24. Указанная связь дает альтернативный способ вычисления последовательности S(n, k). ð Числа Белла. Определение. Общее число разбиений множества X, |X| = n на произвольные классы называется числом Белла и обозначается B(n). Таким образом по определению:
Положим по определению B(0) = 1. Формула 3.
Доказательство. Напомним, что S(n, m)= 0 при m>n. Тогда имеем следующую последовательность очевидных равенств:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

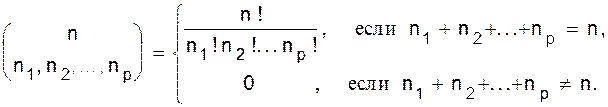
 различными способами, после чего ящик Y2можно наполнить
различными способами, после чего ящик Y2можно наполнить 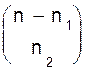 способами и так далее.
способами и так далее.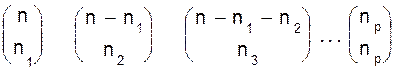 =
=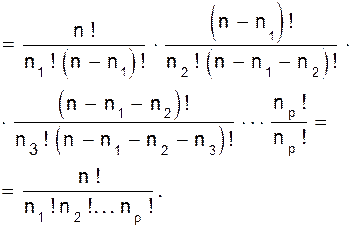
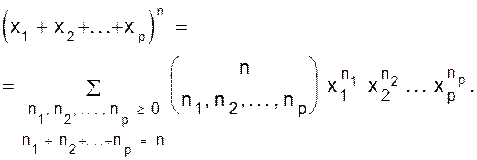 (1.10)
(1.10) равен числу способов выбрать из n сомножителей n1сомножителей, из которых в произведение войдет переменная x1, n2сомножителей, из которых в произведение войдет переменная x2, и так далее. ð
равен числу способов выбрать из n сомножителей n1сомножителей, из которых в произведение войдет переменная x1, n2сомножителей, из которых в произведение войдет переменная x2, и так далее. ð (1.11)
(1.11) .
.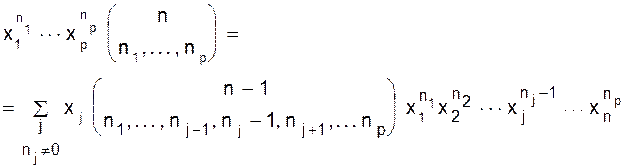

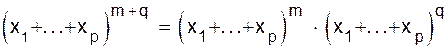 .
.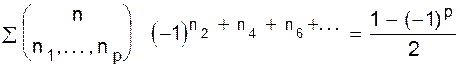 .
.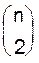 .
. (1.13)
(1.13)
 Y, где |B| = k £ n число сюръективных функций f: X
Y, где |B| = k £ n число сюръективных функций f: X  B в соответствии с утверждением 1.12 равно k! S(n,k). Учитывая, что подмножество B мощности k можно выбрать
B в соответствии с утверждением 1.12 равно k! S(n,k). Учитывая, что подмножество B мощности k можно выбрать 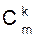 способами получаем формулу:
способами получаем формулу: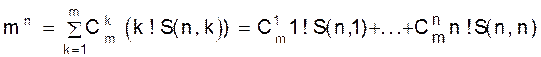 (1.14)
(1.14)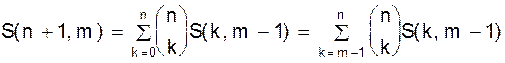
 способами. Таким образом имеем:
способами. Таким образом имеем: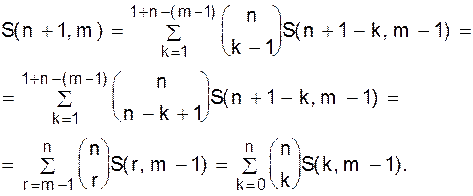
 , (1.15)
, (1.15)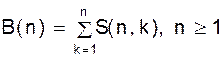 .
.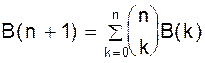 .
.