
|
|
Принцип включений - исключенийЭтот раздел посвящен важному комбинаторному методу - принципу включений-исключений, известному также под названиями: символический метод, принцип перекрестной классификации, метод решета. Логическое тождество, на котором основаны все эти методы, известны давно. Еще в 1713 году Монмор эффективно использовал упомянутый метод в решении знаменитой задачи о встречах (о числе перестановок из n элементов, в которых ни один элемент не сохраняет своей позиции). Принцип включений - исключений - одно из фундаментальных средств перечислительной комбинаторики. Красота этого принципа лежит не в самом результате, а в его широкой применимости. Принцип включений-исключений в перечислительной комбинаторике есть метод определения мощности множества S, который начинает с большего множества и каким-либо путем вычитает или аннулирует нежелательные элементы. Сначала дается приблизительный ответ, содержащий большее число элементов, затем вычитается число элементов, большее чем ошибка, полученная на первом шаге, пока мы не придем к правильному ответу. Это комбинаторная сущность принципа включения-исключения. Для примера рассмотрим принцип включений- исключений в теоретико множественной форме. Пусть даны два конечных множества A и B. Тогда çAÇBç= çAç + çBç - çAÈBç. Чтобы вычислить количество элементов в объединении двух множеств, мы сначала вычисляем сумму их мощностей, но при этом дважды учитываем каждый элемент, принадлежащий пересечению множеств. Вычитая мощность пересечения, приходим к правильному ответу. Совершенно аналогичные рассуждения позволяют выписать формулу для количества элементов в объединении трех множеств A, B, и C: çAÇBÇСç= çAç + çBç +çСç - çAÈBç - çAÈСç - çBÈCç + çAÈBÈCç. Вычитая дважды учтенные элементы попарных пересечений, мы трижды вычли элементы, принадлежащие пересечению всех трех множеств. Добавление мощности пересечения AÈBÈC приводит к нужному результату. Пусть имеется N объектов и n различных свойств a1, a2,..., an. Каждый из объектов может обладать любым из этих свойств (в любом наборе), т.е. обладать любым набором этих свойств, или не обладать никаким из свойств. Пусть N(a1) - число объектов обладающих свойством a1. Некоторые из этих объектов могут обладать и другими свойствами в дополнение к a1, но это неважно. (На самом деле в этом и состоит вся идея метода включений-исключений). Пусть теперь N(a2) - число объектов, обладающих свойством В общем случае пусть N Пусть N0- число предметов, не обладающих ни одним из свойств a1,..., an. Пусть Теорема 1.13. ( Формула включений - исключений).
Прежде, чем переходить к доказательству, вернемся к ранее рассмотренному примеру с тремя множествами A, B, C. Пусть свойством a1обладают все элементы множества A, свойством a2обладают все элементы множества B, свойством a3- все элементы, принадлежащие множеству C. Тогда очевидно, что количество элементов, не обладающих ни одним из свойств a1 , a2 , a3 , равно 0 (каждый элемент принадлежит хотя бы одному из множеств), и в соответствии с формулой (1.16) имеем
Доказательство. Доказательство проводится индукцией по n - числу свойств. При одном свойстве a формула очевидна. Каждый объект либо обладает этим свойством, либо не обладает им. Поэтому N0= N - N(a). Предположим теперь, что для случая, когда число свойств равно n-1, формула доказана: N0= N - N(a1) - ... - N(an-1) + N(a1,a2) + ... + N(an-2, an-1) + + (-1)n-1 N(a1, a2 ,..., an-1). (1.17) Отметим очевидное соотношение:
Формула (1.17) по предположению справедлива для любой совокупности объектов. В частности она верна для совокупности
Вычтем равенство (1.19) из (1.17). В правой части получим то, что нужно - правую часть формулы включения-исключения, а в левой части получим разность (1.18). Тем самым формула (1.16) доказана. ð Для того, чтобы облегчить всестороннее использование этой формулы, сделаем следующие замечания. Во-первых, лучше всего она запоминается в следующей “символической записи”:
Сначала вычисляется содержимое квадратных скобок, а затем знак функции N применяется к слагаемым: N[a+b]= N(a)+N(b), N[-a]=-N(a), N[1]=N, N[(1-a)(1-b)]=N(1-a-b+ab)=N-N(a)-N(b)+N(a,b). Далее, как видно из доказательства формулы включений - исключений, совокупности объектов, к которым применима теорема, не обязана быть совокупностью N всех объектов. Поэтому N(a1 -N(a1a3a4) + N(a1a2a3a4). Вообще, если n различных свойств a1,...,anобъектов из совокупности N объектов обозначить
Рассмотрим принцип включений- исключений в несколько более общей форме. Пусть S - множество свойств, которыми элементы данного множества A могут обладать, а могут не обладать. Для любого подмножества T множества S, TÍS, пусть N=(T) - число объектов множества A, которые обладают в точности свойствами из T (так что они не обладают никакими другими свойствами из
где Y пробегает все подмножества множества S. В типичных приложениях принципа включений-исключений относительно легко вычислить N³(Y) для YÍS, так что нами получена окончательная формула для N= (T). Распространенным частным случаем принципа включения-исключения является выполнение условия N=(T) = N=(T¢), как только êT ê= ê T¢ ê. В рассматриваемом частном случае количество объектов, обладающих в точности заданным множеством свойств, зависит не от конкретного набора свойств, а только от числа рассматриваемых свойств. таким образом, N³(T) зависит также только от çT ç и мы полагаем a(n - i) = N=(T) (1.22) и b(n - i) = N³(T), (1.23) если êT ê= i. Из формул (1.20) и (1.21) получаем, что формулы
и
эквивалентны. Это еще одно отражение комбинаторных соотношений взаимности. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 - число объектов, обладающих свойствами
- число объектов, обладающих свойствами  (и, быть может, некоторыми другими).
(и, быть может, некоторыми другими). - число объектов, не обладающих свойством a1. Чертой над символом свойства будем указывать, что речь идет об объектах, не обладающих таким свойством. Тогда в принятом обозначении N0= =
- число объектов, не обладающих свойством a1. Чертой над символом свойства будем указывать, что речь идет об объектах, не обладающих таким свойством. Тогда в принятом обозначении N0= = 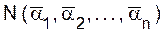 .
.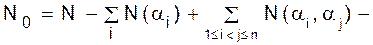
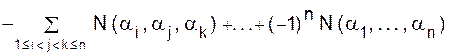 . (1.16)
. (1.16)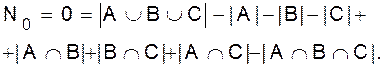
 (1.18)
(1.18)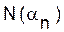 элементов, обладающих свойством an. Применим индуктивное предположение к совокупности N(an) для вычисления
элементов, обладающих свойством an. Применим индуктивное предположение к совокупности N(an) для вычисления 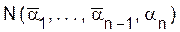 :
: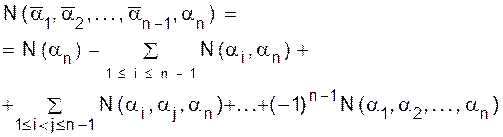 (1.19)
(1.19)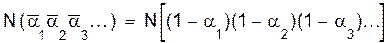
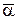 2a3
2a3 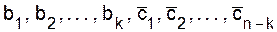 , то
, то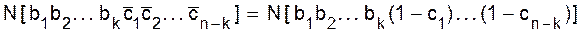 .ð
.ð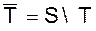 ). Пусть N³(T) - число объектов множества A, обладающих по меньшей мере свойствами из T (и, возможно, какими-то другими свойствами). Ясно, что тогда
). Пусть N³(T) - число объектов множества A, обладающих по меньшей мере свойствами из T (и, возможно, какими-то другими свойствами). Ясно, что тогда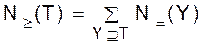 , (1.20)
, (1.20) , (1.21)
, (1.21) ,
, , (1.24)
, (1.24)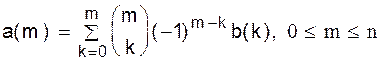 , (1.25)
, (1.25)