|
|
Гамильтоновы пути и циклыРассмотрим теперь задачу предыдущего раздела с той лишь разницей, что на этот раз нас будут интересовать пути, проходящие в точности один раз через каждую вершину (а не каждое ребро) данного графа. Эта небольшая, как может показаться, модификация приводит к значительному изменению характера проблемы. Простой путь (цикл) называется гамильтоновым путем (циклом), если он проходит через каждую вершину графа. Слово “гамильтонов” в этих определениях связано с именем известного ирландского математика У. Гамильтона, который в 1859 г. предложил игру “Кругосветное путешествие”. В этой игре мир представлен додекаэдром, каждой вершине которого приписано название одного из городов мира. Требуется, переходя из одного города в другой по ребрам додекаэдра, посетить каждый город в точности один раз и вернуться в исходный город.
Более толстыми линиями на графе додекаэдра выделен гамильтонов путь. Укажем аналогичным выделением гамильтонов путь для следующего графа:
С другой стороны, легко видеть, что в следующем графе не существует гамильтоновых путей:
В отличие от эйлеровых путей не известно ни одного простого необходимого и достаточного условия для существования гамильтоновых путей и циклов, и это несмотря на то, что задача - одна из центральных в теории графов. Не известен так же алгоритм, который проверял бы существование гамильтонова пути в произвольном графе, используя число шагов, ограниченное многочленом от переменной n (числа вершин в графе). Имеются веские основания, но нет математических доказательств того, чтобы предполагать, что такое положение вызвано не нашим незнанием, а скорее тем фактом, что такого алгоритма не существует. Проблема существования гамильтонова пути принадлежит к классу так называемых NP - полных задач. Это широкий класс задач, включающий задачи из теории графов, логики, теории чисел, дискретной оптимизации, ни для одной из которых не известен полиномиальный алгоритм (то есть алгоритм с числом шагов, ограниченным полиномом от размерности задачи). В применениях графов к играм вершины соответствуют различным позициям. Существование гамильтонова цикла равносильно существованию циклической последовательности ходов, содержащей каждую позицию по одному разу. (Пример - задача о шахматном коне: можно ли, начиная с произвольного поля доски, ходить конем так, чтобы пройти через все поля и вернуться в исходное.) Выведем некоторые условия, при которых можно утверждать, что гамильтонов цикл существует. Эти рассмотрения тесно связаны со свойствами максимальных простых путей. Пусть Определим подграф Будем говорить, что S имеет тип цикла, если подграф
имеет гамильтонов цикл. Отсюда, в частности, следует, что S является гамильтоновым путем в G0 . Пусть
Если, однако, Будем говорить, что простой путь - полный, если его нельзя продолжить при помощи добавления ребер к какому-нибудь из концов. Тогда все ребра от a0и от akдолжны идти к вершинам графа G0, так что Это дает следующую теорему. Теорема 3.13.Полный простой путь длины k имеет тип цикла, если
Теорема 3.14.Максимальный простой путь в связном графе может иметь тип цикла только тогда, когда граф имеет гамильтонов цикл. Доказательство. 1). Если G имеет гамильтонов цикл, то максимальный простой путь длины n-1 имеет тип цикла. 2). Если подграф G0, соответствующий максимальному простому пути имеет гамильтонов цикл, но G0не составляет всего графа, то из-за связности G существует некоторое ребро Теорема 3.15. В связном графе либо имеется гамильтонов цикл, либо длина его максимальных простых путей удовлетворяет неравенству
Из последнего условия вытекает, что Теорема 3.16. В графе без гамильтоновых циклов длина его максимальных простых путей k удовлетворяет неравенству В теореме 3.16 можно не предполагать, что граф связен. Отметим еще, что в графе с n вершинами максимальный простой путь имеет длину, не превышающую n-1. Как частный случай приведенных результатов получается следующая теорема. Теорема 3.17.Если в графе G с n вершинами для любой пары вершин a0и ak имеет место соотношение Если Отсюда, в частности, следует результат Дирака о том, что граф с n вершинами имеет гамильтонов цикл, если для каждой его вершины Определение.Будем называть неориентированный простой граф k- связным, если наименьшее число вершин, удаление которых приводит к несвязному или одновершинному графу, равно k. ð Случаи, когда k = 2 или k =3 в теории графов имеют особую роль. Такие графы фигурируют во многих теоретических и прикладных вопросах, в частности ряд задач достаточно уметь решать для 2-связных компонент; кроме того, при k =3 и, особенно при k = 2 удается дать достаточно обозримое описание соответствующих графов. Рассмотрим сначала некоторые простые свойства 2-связных графов, вытекающие непосредственно из определения: 1. степени вершин двусвязного графа больше единицы; 2. если графы G1и G22-связны и имеют не менее двух общих вершин, то граф G1ÇG2также 2-связен; 3. назовем точкой сочленения графа такую его вершину, удаление которой приводит к графу с большим числом компонент связности; если вершина v графа не является точкой сочленения графа, то любые две его вершины соединены путем, не содержащим v; в частности, в 2-связном графе для любых трех несовпадающих вершин a, b, v имеется путь из вершины a в вершину b, не проходящий через вершину v. Будем в дальнейшем графы, имеющие гамильтонов цикл, называть гамильтоновыми. Гамильтонов граф должен быть двусвязным. Однако пример графа, представленный на следующем рисунке, показывает, что для гамильтоновости графа двусвязности недостаточно.
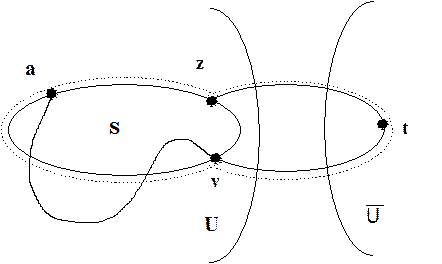
Рис. 3.6. Любой граф, содержащий две вершины степени 3, соединенных тремя простыми попарно непересекающимися путями длины не менее двух, называется тэта-графом. Пример тэта-графа приведен на рис. 3.6. Далее будет доказана теорема о том, что каждый негамильтонов двусвязный граф содержит тэта-подграф. Но прежде чем переходить к доказательству этого результата, остановимся на необходимом для него утверждении относительно двусвязных графов, представляющем и самостоятельный интерес. Теорема 3.18.Пусть G =<V, E> - связный граф и количество его вершин |V|>2. Тогда следующие утверждения эквивалентны: 1) граф 2-связен; 2) любые две вершины графа принадлежат простому циклу; 3) любая вершина и любое ребро принадлежат простому циклу; 4) любые два ребра принадлежат простому циклу; 5) для любых двух вершин a и b и любого ребра e существует простой 6) для любых трех вершин a, b, c существует простой (a, b)-путь, проходящий через с. Доказательство. 1) Þ 2). Пусть a и b - две вершины графа G. Рассмотрим множество всех простых циклов графа G, содержащих вершину a. Обозначим через U множество всех вершин, входящих в эти циклы. Ясно, что U ¹ Æ. Действительно, простой цикл, содержащий a, можно получить, объединив два ребра (a, x) и
Рис. 3.7. 2) Þ 3). Пусть a - вершина и (x, t) - ребро графа . По условию G cодержит цикл S, проходящий через вершины a и x. Не теряя общности будем считать, что ребро (x, t) Ï S. Если при этом окажется, что S проходит через вершину t, то требуемый цикл строится очевидным образом. Пусть S не проходит через вершину t. Тогда рассмотрим простой цикл, проходящий через вершины t и a. Такой цикл, по условию, существует. Частью этого цикла является простой путь P, соединяющий t с некоторой вершиной v Î S. Путь P можно выбрать так, чтобы пути P и S пересекались только в вершине v. Искомый цикл строится точно так же, как в предыдущем пункте. 3) Þ 4). Пусть (a, b) и (t, z) - два ребра графа G. По условию G имеет простые циклы S и S¢ , первый из которых содержит ребро (a, b) и вершину z, а второй - (a, b) и t. Далее искомый цикл строится точно так же, как в предыдущих пунктах. 4) Þ 5). Пусть a и b - вершины графа G, и (t, z) - его ребро. Будучи связным, граф G содержит простой путь P = (a, x, ... , b). Согласно утверждению 4), в графе G есть простой цикл S, содержащий ребра (a, x) и (t, z). Легко видеть, что в объединении S Ç P имеется требуемый путь. 5) Þ 6). Пусть a, b, c - вершины графа G, (c, d) - его ребро. По условию в графе имеется простой (a, b) - путь, проходящий через (c, d), и следовательно, содержащий c. 6) Þ 1). Пусть v- вершина графа G. Покажем, что граф G с удаленной вершиной v ( граф G\{v}) - связен, т.е. любая пара a, b его вершин соединена путем. Действительно, согласно утверждению 6) в графе G имеется простой Теорема 3.19. Каждый негамильтонов двусвязный граф содержит тэта-подграф. Доказательство. Пусть G = <V, E> - негамильтонов двусвязный граф и C - простой цикл максимальной длины в этом графе. По условию теоремы множество S вершин графа G, не принадлежащих циклу S, непусто. Как подтверждает прямая проверка, среди двусвязных графов, порядок которых меньше пяти, нет негамильтоновых, поэтому ½V½³ 5. Из двусвязности графа и теоремы 3.18 следует, что количество вершин в цикле C не менее четырех. Пусть (x, v) - такое ребро графа G, что x Î C, v Î S, a и b - вершины цикла C, смежные с x (см. рис. 3.8). Поскольку С - максимальный цикл, то вершина v не смежна ни с a, ни с b (иначе можно было бы построить больший цикл). Рассмотрим теперь граф G\{x}, который, очевидно, связен. В этом графе для каждой вершины y Î C, имеется (v, y)- путь. Выберем их этих путей кратчайший (v, y*)-путь P*. Учитывая, что C - максимальный цикл, имеем
Рис. 3.8. Степенной последовательностью графа будем называть последовательность степеней его вершин. Теорема 3.20.Граф со степенной последовательностью d1£ d2£ ... £ dnявляется гамильтоновым, если для всякого k, удовлетворяющего неравенствам 1£ k < n/2, истинна импликация (dk £ k ) Þ( dn - k ³ n - k ). Доказательство этой теоремы здесь не приводится.ð В радиоэлектронике и микроэлектронике, в задачах проектирования железнодорожных и других путей, где нежелательны пресечения и переезды, возникает понятие плоского графа. Плоским графом называется граф, вершины которого являются точками плоскости, а ребра - непрерывными плоскими линиями без самопересечений, соединяющими соответствующие вершины так, что никакие два ребра не имеют общих точек, кроме инцидентной им обоим вершины. Любой граф, изоморфный плоскому графу, называется планарным графом. Следующая теорема - один из наиболее сильных результатов, касающихся гамильтоновых графов. Теорема 3.21.Всякий 4-связный планарный граф является гамильтоновым. Весьма сложное доказательство этой теоремы здесь не приводится.ð Пусть G = <V, E> - связный граф, u, v - две его несовпадающие вершины. Длина кратчайшего (u, v) - пути (он, естественно, является простым путем) называется расстоянием между вершинами u и v и обозначается через d(u, v). Понятие расстояния между вершинами в связном графе позволяет определить k-ую степень графа. Пусть G - связный граф, k - натуральное число. Граф Gk имеет то же множество вершин, что и G, несовпадающие вершины u и v смежны в графе Gk тогда и только тогда, когда для графа G верно неравенство Интуитивно ясно, что если граф порядка n = |V| ³ 3 связен, то при достаточно больших k граф Gk гамильтонов. Приведем без доказательства две теоремы, касающиеся гамильтоновости степеней графа. Теорема 3.22.Если граф G порядка n = |V| ³ 3 связен, то G3 - гамильтонов граф. Теорема 3.23.Если G - двусвязный граф порядка n = |V| ³ 3, то G2 - гамильтонов граф. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|



 - некоторый простой путь длины k в графе G = <V, E >.
- некоторый простой путь длины k в графе G = <V, E >. .
. .
. - некоторое ребро в графе G0 . Если существует также ребро
- некоторое ребро в графе G0 . Если существует также ребро  , то в G0будет гамильтонов цикл, а именно
, то в G0будет гамильтонов цикл, а именно

 , где r0(a0) и r0(ak) степени вершин a0и akв графе G0, то ясно, что хотя бы для одного ребра
, где r0(a0) и r0(ak) степени вершин a0и akв графе G0, то ясно, что хотя бы для одного ребра 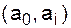 должно существовать соответствующее ребро
должно существовать соответствующее ребро 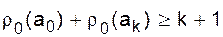 , то простой путь S будет иметь тип цикла.
, то простой путь S будет иметь тип цикла. ,
,  .
. .
.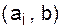 , в котором b не принадлежит G0. Это, однако, невозможно так как тогда нашелся бы простой путь, который был бы длиннее данного простого пути S. Из двух доказанных утверждений следует
, в котором b не принадлежит G0. Это, однако, невозможно так как тогда нашелся бы простой путь, который был бы длиннее данного простого пути S. Из двух доказанных утверждений следует . ð
. ð для всех пар вершин a0и ak, причем можно даже ограничиться теми парами, для которых нет ребра
для всех пар вершин a0и ak, причем можно даже ограничиться теми парами, для которых нет ребра  Отсюда следует
Отсюда следует где r1и r2- две наименьшие степени вершин. ð
где r1и r2- две наименьшие степени вершин. ð , то граф G имеет гамильтонов путь.
, то граф G имеет гамильтонов путь. , то G имеет гамильтонов цикл. ð
, то G имеет гамильтонов цикл. ð

 . Поскольку граф G связен, то в нем найдется такое ребро (x, t), что
. Поскольку граф G связен, то в нем найдется такое ребро (x, t), что  (рис. 3.7). Пусть S- простой цикл, содержащий a и x. Так как G-двусвязный граф, то в нем имеется простой (a, t)-путь P, не содержащий x. Пусть v - первая, считая от t, вершина, входящая в S, т.е. (t, v)-подпуть пути P не имеет с S общих вершин, отличных от v. Теперь легко построить простой цикл, содержащий v и t. Он получается объединением (v, z)- пути, проходящего через a и являющегося частью S, с ребром (z, t) и (t, v) -частью пути P (на рис. 3.7 этот цикл показан пунктирной линией). Следовательно, t Î U, но это противоречит выбору ребра (x, t). Таким образом
(рис. 3.7). Пусть S- простой цикл, содержащий a и x. Так как G-двусвязный граф, то в нем имеется простой (a, t)-путь P, не содержащий x. Пусть v - первая, считая от t, вершина, входящая в S, т.е. (t, v)-подпуть пути P не имеет с S общих вершин, отличных от v. Теперь легко построить простой цикл, содержащий v и t. Он получается объединением (v, z)- пути, проходящего через a и являющегося частью S, с ребром (z, t) и (t, v) -частью пути P (на рис. 3.7 этот цикл показан пунктирной линией). Следовательно, t Î U, но это противоречит выбору ребра (x, t). Таким образом  , т.е. a и b принадлежат одному общему простому циклу.
, т.е. a и b принадлежат одному общему простому циклу.