
|
|
Разложение функций алгебры логики по переменнымГоворя о языке формул, мы сознательно не касались весьма важного вопроса: всякая ли функция алгебры логики может быть выражена в виде формулы, если допустить некоторый запас элементарных функций? Ближайшие рассмотрения направлены на решение этого вопроса. Чтобы иметь возможность единообразно записывать переменные с отрицанием и без отрицания введем следующее обозначение:
Легко видеть, что xs = 1 тогда и только тогда, когда x = s, то есть значение “основания” равно значению “показателя”. Лемма 2.2.(О разложении функции по одной переменной). Пусть f(x1, ... , xn) - произвольная функция алгебры логики, тогда справедливо следующее представление f в форме разложения по переменной x1:
Доказательство. Отметим прежде всего, что представление (2.1), естественно, справедливо для произвольной переменной xiиз множества переменных функции f. Для доказательства рассмотрим произвольный набор значений переменных (a1, ... , an) и покажем, что левая и правая части соотношения (2.1) принимают на нем одно и то же значение. Рассмотрим набор значений переменных (1, a2, ... , an). Левая часть (2.1) принимает на этом наборе значение f(1, a2,..., an), а правая часть - значение 1×f(1, a2, ... , an ) Ú 0×f(0, a2, ... , an) = f (1, a2, ... , an ). Таким образом, на наборах (1, a2, ... , an) левая и правая части (2.1) принимают одинаковые значения. Рассмотрим набор значений переменных (0, a2, ... , an). Левая часть (2.1) принимает на этом наборе значение f(0, a2,..., an), а правая часть - значение 0×f(1, a2, ... , an ) Ú 1×f (0, a2, ... , an) = f (0, a2, ... , an ). Таким образом, на наборах (0, a2, ... , an) левая и правая части (2.1) принимают одинаковые значения. Тем самым мы доказали, что левая и правая части соотношения (2.1) принимают одинаковые значения на всех наборах (a1, ... , an). ð Лемма 2.3. Конъюнкция (произведение) Доказательство. Произведение (конъюнкция) равно 1 тогда и только тогда, когда каждый сомножитель равен 1, но xs = 1 тогда и только тогда, когда x = s. ð В дальнейшем будем употреблять следующие обозначения:
Эти записи имеют смысл и при k = 1. Теорема 2.4. (О разложении функции по нескольким переменным).
Доказательство. Рассмотрим произвольный набор значений переменных (a1, ... , an) и покажем, что левая и правая части соотношения (2.2) принимают на нем одно и то же значение. Левая часть дает f(a1,..., ak,a k+1 ,..., an). Правая часть дает
Представление (2.2) называется дизъюнктивным разложением функции по kпеременным. Пример. Для k = 2 разложение в дизъюнктивную форму имеет вид:
Выпишем такое разложение для конкретной функции трех переменных по переменным x2и x3:
В качестве следствий получаем два специальных разложения. 1. Разложение по одной переменной, выписанное ранее. 2. Разложение по всем n переменным. Если k = n, то получаем разложение
Оно может быть преобразовано при f(x1, ... , xn) ¹ 0 следующим образом:
Итак, в этом случае разложение имеет вид:
Это разложение называется совершенной дизъюнктивной нормальной формой (совершенная ДНФ.). Оно определено для любой функции f, не равной константе 0. Теорема 2.5. Произвольную функцию алгебры логики можно выразить формулой при помощи операций Ù, Ú, ù , причем операция ù применяется только к переменным. Доказательство. 1. Пусть f(x1, ... , xn) = 0. Тогда, очевидно, f(x1, ... , xn) = x1 Ù ù x1. 2. Пусть f(x1, ... , xn) ¹ 0. Представим ее в форме совершенной ДНФ.:
Таким образом, в обоих случаях функция f выражается в виде формулы через конъюнкцию, дизъюнкцию и отрицание, причем отрицание применяется только к символам переменных. ð Итак, оказалось, что любую булеву функцию можно выразить формулой над множеством операций {Ù, Ú, ù }, состоящим из трех функций: отрицания, конъюнкции и дизъюнкции. Данная теорема носит конструктивный характер, так как она позволяет для каждой функции построить реализующую ее формулу (совершенную ДНФ). А именно, берем таблицу для функции f(x1, ... , xn) (f¹ 0) и отмечаем в ней все строки (s1, ... , sn), в которых f(s1, ... , sn) =1, для каждой такой строки образуем логическое произведение Пример. Построить совершенную ДНФ для функции, заданной таблицей:
Имеем:
Если в таблице значений функции много 1 и мало 0, то целесообразно строить функцию по-другому. Совершенная ДНФ есть выражение типа “Ú &”, то есть логическая сумма произведений Аналогично только что проведенным доказательствам легко получить, что: * * * имеет место следующее разложение в конъюнктивную нормальную форму по одной переменной f (x1,..., xn ) = (x1 * имеет место следующее представление функции в виде совершенной конъюнктивной нормальной формы (совершенная КНФ) для f ¹1:
Использование совершенной КНФ позволяет упростить запись формулы для функции, таблица значений которой содержит мало нулей. ÿ Кроме отмеченных конъюнктивного и дизъюнктивного разложений функции по переменной часто используется и разложение, основанное на операции логической суммы:
Последовательное применение такого разложения ко всем переменным позволяет выразить произвольную функцию алгебры логики через элементарные функции 2.5. Функциональная полнота систем функций алгебры Выше мы видели, что всякая функция алгебры логики может быть выражена в виде формулы через элементарные функции Прежде всего уточним, какими средствами из имеющейся системы функций можно получать новые функции. Новые функции получаются из имеющихся в заданной системе функций с помощью операций замены переменных и суперпозиции. Опишем эти две операции. Замена переменных. Пусть f(x1, x2, ... , xn) - заданная функция алгебры логики. Будем говорить, что функция j(y1, y2, ... , yn) получена операцией замены переменных из функции f(x1, x2, ... , xn), если осуществлена подстановка переменных
то есть вместо каждого вхождения переменой x1подставляется переменная y1, вместо каждого вхождения переменой x2подставляется переменная y2, ... , вместо каждого вхождения переменой xnподставляется переменная yn , при этом yi не обязана отличаться от ykпри i¹k . Очевидно, что замена переменных включает в себя переименование переменных, перестановку переменных и отождествление переменных. Пример.Пусть имеется функция 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
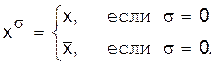
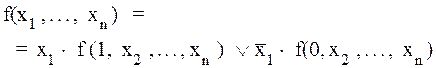 (2.1)
(2.1) тогда и только тогда, когда
тогда и только тогда, когда 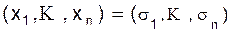 .
.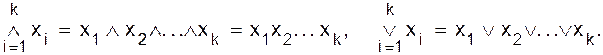
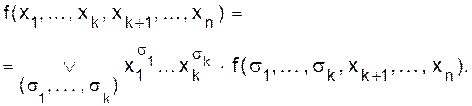 (2.2)
(2.2) ð
ð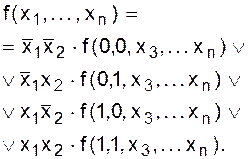
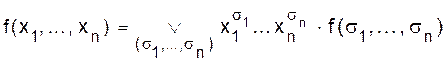

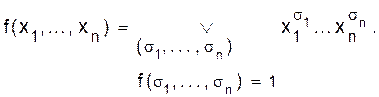
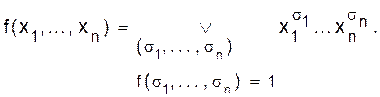
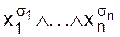 , а затем соединяем все полученные конъюнкции знаком дизъюнкции.
, а затем соединяем все полученные конъюнкции знаком дизъюнкции.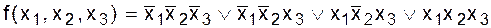 . ð
. ð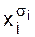 . Спрашивается нельзя ли для функции алгебры логики получить разложение типа “& Ú “?
. Спрашивается нельзя ли для функции алгебры логики получить разложение типа “& Ú “? 
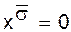 тогда и только тогда, когда x = s;
тогда и только тогда, когда x = s;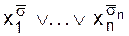 обращается в 0 только на наборе (x1, ... , xn) = (s1, ... , sn);
обращается в 0 только на наборе (x1, ... , xn) = (s1, ... , sn);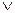 f (0, x2,..., xn )) (
f (0, x2,..., xn )) ( 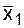
 .
. .
. , x+y, xÙy или, используя соотношение
, x+y, xÙy или, используя соотношение 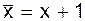 , лишь через функции x+y, xÙy, 1.
, лишь через функции x+y, xÙy, 1.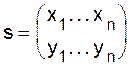 ,
, . Тогда при замене переменных
. Тогда при замене переменных 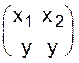 из функции
из функции 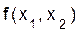 можно получить функцию
можно получить функцию  .
.