
|
|
Алгоритм построения остовного дерева методом поиска в глубину.Исходные данные: связный граф G =<V, E>, заданный списками инцидентности ЗАПИСЬ[v], vÎV. Результат: каркас <V, T> графа G. Алгоритм. 1 procedure КАРКАС_ГЛУБИНА(v) {поиск в глубину из вершины v, соединенный с нахождением ребра дерева; переменные НОВЫЙ, ЗАПИСЬ, T - глобальные} 2 beginНОВЫЙ[v] := ложь; 3 foruÎЗАПИСЬ[v] do 4 ifНОВЫЙ[u] then{ (u, v) - новая ветвь} 5 begin T := T Ç (v, u); КАРКАС_ГЛУБИНА(u) 6end 7 end{вершина v использована}; 8 begin { главная программа} 9 foru Î V doНОВЫЙ [u] := истина; { инициализация} 10 T := Æ; { T - множество найденных к этому времени ребер каркаса} 11 КАРКАС_ГЛУБИНА(r) {r - произвольная вершина графа } End Для доказательства того, что приведенный алгоритм правильно строит каркас произвольного связного графа, достаточно отметить следующие три факта. Во-первых, в момент добавления к множеству T нового ребра (v, u) в строке 5 в <V, T> существует путь из r в v (этот факт легко доказывается по индукции). Таким образом, алгоритм строит связный граф. Во-вторых, каждое новое ребро (v, u), добавляемое ко множеству T, соединяет уже рассмотренную вершину v (т.е. НОВЫЙ [v] = ложь) с новой вершиной u. Отсюда следует, что построенный граф <V, T> не содержит циклов. Действительно, последнее ребро, “замыкающее” цикл, должно было бы соединить две уже рассмотренные вершины. И, наконец, в-третьих, из свойства поиска в глубину следует, что процедура КАРКАС_ГЛУБИНА просматривает все вершины связного графа. Следовательно, граф <V, T>, построенный нашим алгоритмом, есть остовное дерево графа G. Вычислительная сложность алгоритма есть, очевидно, O(n+m), т.е. того же порядка, что и сложность поиска в глубину. Аналогично выглядит процедура построения остовного дерева методом поиска в ширину. Алгоритм построения остовного дерева методом поиска в ширину. Исходные данные: связный граф G =<V, E>, заданный списками инцидентности ЗАПИСЬ[v], vÎV. Результат: каркас <V, T> графа G. Алгоритм. Begin 2 foru Î V do НОВЫЙ [u] := истина; { инициализация} 3T := Æ; { T -множество найденных к этому времени ребер каркаса} 4 ОЧЕРЕДЬ := Æ; ОЧЕРЕДЬ Ü r; 5 НОВЫЙ [r]:= ложь; { r - корень каркаса} 6 whileОЧЕРЕДЬ ¹ Æ do 7 beginp Ü ОЧЕРЕДЬ; 8 foru Î ЗАПИСЬ [ v] do 9 ifНОВЫЙ [ u] then 10 beginОЧЕРЕДЬ Ü u; НОВЫЙ [ u ]:= ложь; T := T Ç (v, u); End End End . Рассуждениями, аналогичными проведенным для алгоритма КАРКАС _ ГЛУБИНА, можно показать, что данный алгоритм корректно строит остовное дерево для призвольного связного графа за O(n+m) шагов. На следующем рисунке дан пример остовного дерева для графа, построенного методом поиска в ширину (а) и в глубину (б).
(а) (б)
Каждое остовное дерево, построенное с помощью метода поиска в глубину, имеет любопытное свойство, которое сейчас будет описано. Вершину r, из которой начинается поиск, назовем корнем остовного дерева. Для двух различных вершин v и u дерева < V, T > будем говорить, что u является потомком вершины v, если v лежит на пути (в дереве < V, T >) из вершины u в вершину v. Теорема 3.9.. Пусть < V, T > - остовное дерево связного графа неориентированного графа G = < V, E >, построенное с помощью алгоритма КАРКАС _ ГЛУБИНА, и пусть (u, v) Î E. Тогда либо u - потомок v, либо v - потомок u. Доказательство. Предположим без ограничения общности, что вершина v будет просмотрена раньше, чем u. Рассмотрим процесс поиска в глубину, начиная с вершины v. Очевидно, что по окончании его должно быть НОВЫЙ [u] = ложь, ибо (v, u) - ребро. Но это означает, что ребра, добавленные во множество T в течение этого процесса, содержат путь из v в u, откуда следует, что v лежит на пути из u в корень, поскольку в дереве существует в точности один путь из произвольной вершины к корню.ð Рассуждения, проведенные в предыдущем разделе, непосредственно приводят к следующей теореме. Теорема 3.10.Пусть < V, T > - остовное дерево связного графа неориентированного графа G = < V, E >, построенное с помощью алгоритма поиска в ширину. Тогда путь в < V, T > из произвольной вершины v до корня r является кратчайшим путем из v в r в графе G. Далее особо обсуждается более общая задача отыскания кратчайших путей в графе, ребрам которого приписаны “длины” (веса), не обязательно равные единице. Эйлеровы пути и циклы Задача о кенигсбергских мостах послужила началом теории графов. План расположения семи мостов в Кёнигсберге (ныне г. Калининград) приведен на рис. 3.5.
Рис. 3.5. Задача состоит в том, чтобы пройти каждый мост по одному разу и вернуться в исходную точку С. Так как существенны только переходы через мосты, план города можно свести к изображению графа, в котором ребра соответствуют мостам, а вершины - разделенным частям города.
Очевидно, не существует циклических обходов, проходящих по всем ребрам по одному разу. Развлечения, в которых требуется обрисовать некоторую фигуру, не прерывая и не повторяя линии, являются, по-видимому, очень давними. Считается, что фигура, называемая саблями Магомета, имеет арабское происхождение.
Эйлер обратился к общей задаче, касающейся графов: в каких случаях в конечном графе можно найти такой цикл, в котором каждое ребро участвовало бы один раз? Эйлеровым путем в графе G = < V, E >называется произвольный путь, проходящий через каждое ребро графа в точности один раз, т.е. путь Теорема 3.11.Эйлеров путь в неориентированном простом графе существует тогда и только тогда, когда граф связный и содержит не более, чем две вершины нечетной степени. ð Если в связном графе нет вершин нечетной степени, то каждый эйлеров путь является циклом, так как концы эйлерова пути, не являющегося циклом, всегда вершины нечетной степени. Предположим, что u и v - единственные вершины нечетной степени в связном графе G = <V, T >и образуем граф G¢ добавлением дополнительной вершины t и ребер {u,v} и {v,t} (или просто добавлением ребра {u,v}, если Теорема 3.12.Конечный граф G = <V, E >содержит эйлеров цикл тогда и только тогда, когда 1. G - связен. 2. Все степени его вершин четные. Доказательство. Условие 1, очевидно, необходимо. Далее, каждый раз, когда эйлеров цикл проходит через какую-то вершину, он должен войти в нее по одному ребру и выйти по другому; поэтому условие 2 также необходимо. Предположим теперь, что эти два условия выполнены. Начнем путь Рв произвольной вершине аграфа G и будем продолжать его, насколько возможно, всё время через новые рёбра. Так как степени всех вершин четны, этот процесс может закончится только в вершине а. Если Р содержит не все рёбра графа G, то удалим из G часть Р, состоящую из ребер этого цикла. Графы Р и G имеют четные степени вершин, то же будет справедливо и для остающегося графа Так как граф G связен, в Р должна найтись вершина b, инцидентная также ребрам из
который возвращается в а и содержит больше ребер, чем Р. Если P1не является эйлеровым циклом, то это построение повторяется. Когда процесс закончится, эйлеров цикл будет построен. ð Представим изложенный процесс построения эйлерова цикла в виде схемы алгоритма на “псевдоалгоритмическом” языке. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|




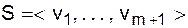 такой, что каждое ребро
такой, что каждое ребро 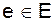 появляется в последовательности
появляется в последовательности  в точности один раз как
в точности один раз как  для некоторого i. Если
для некоторого i. Если  , то такой путь называется эйлеровым циклом. ð
, то такой путь называется эйлеровым циклом. ð ). Тогда G¢ - связный граф без вершин нечетной степени, а эйлеровы пути в G будут в очевидном взаимно однозначном соответствии с эйлеровыми циклами в G¢. В силу этого мы будем заниматься только эйлеровыми циклами и переформулируем теорему.
). Тогда G¢ - связный граф без вершин нечетной степени, а эйлеровы пути в G будут в очевидном взаимно однозначном соответствии с эйлеровыми циклами в G¢. В силу этого мы будем заниматься только эйлеровыми циклами и переформулируем теорему.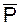 .
. ,
,