
|
|
Перестановки с ограничениями на местоположениеВ задаче о числе беспорядков ищут число перестановок pÎsn, в которых для каждого i некоторые значения p(i) запрещены (именно, p(i) ¹i). Рассмотрим более общую теорию таких перестановок. Традиционно ее описывают, используя шахматную терминологию. Пусть G(p) ={(i, p(i), iÎ[n]}. Определим теперь Nj= ½{pÎsn: j = ½B Ç G(p)½}½, r k= число k - подмножеств множества B, таких, что никакие два элемента не имеют общей координаты, r k= число способов разместить k не атакующих друг друга ладей на B. Мы можем отождествить перестановку pÎsnс размещением n не атакующих друг друга ладей в квадратах (i, p(i)) доски
Теорема 1.15. Имеем
В частности,
Первое доказательство. Пусть Ckесть число пар (p, C), где pÎsn и C - k-подмножество множества B Ç G(p). Для каждого j выберем Nj способами перестановку p так, чтобы j = ½B Ç G(p)½, а затем C выберем
или, эквивалентно,
Полагая y = x - 1, получаем желаемую формулу (1.29). ð Второе доказательство. Достаточно доказать формулу (1.29) в предположении, что x - положительное целое число. Левая часть формулы (1.29) подсчитывает число способов, которыми можно разместить не атакующие ладьи на доске Два доказательства теоремы 1.15 дают еще одну иллюстрацию двух комбинаторных способов доказательства равенства двух многочленов. Конечно, можно доказать формулу (1.30) прямым применением метода включений-исключений. Такое доказательство нельзя было бы рассматривать как комбинаторное, так как мы не построили явно взаимно однозначное соответствие между двумя множествами. Два доказательства, которые приведены выше, можно рассматривать как “полукомбинаторные”, так как они получаются из прямых формул взаимно однозначного соответствия, включающих параметры x и y соответственно, и затем мы получаем формулу (1.30), полагая y = -1 и 1.16. Пример. (Снова задача о беспорядках). Возьмем B={(1, 1), (2, 2), ... , (n, n)}. Мы хотим вычислить N0= D(n). Ясно, что
1.17. Пример. (Задача о супружеских парах (о гостях).) Эта известная задача формулируется следующим образом: сколькими способами можно рассадить за круглым столом n супружеских пар так, чтобы никакая пара не сидела рядом и женщины чередовались с мужчинами. Задача эквивалентна поиску числа перестановок pÎsn, для которых p(i)¹i, i+1(mod n) для всех iÎ[n]. Другими словами, мы ищем число N0для доски B = {(1, 1), (2, 2), ... , (n, n), (1, 2), (2, 3), ... , (n - 1, n), (n, 1)}. Взглянув на рисунок доски B, мы видим, что rk равно числу способов, которыми можно выбрать k из 2n расположенных на окружности точек так, чтобы среди них не было двух последовательных (соседних). Лемма 1.18. Число способов, которыми можно выбрать k точек из m точек на окружности так, чтобы среди них не было двух последовательных (соседних) точек, равно
Первое доказательство. Пусть f(m, k) - искомое число, и пусть g(m, k) - число способов выбрать k не последовательных точек из m точек, расположенных по окружности, а затем покрасить k выбранных точек в красный цвет и одну из неокрашенных точек покрасить в синий цвет. Ясно, что g(m, k) = (m - k)f(m, k). Но можно вычислить g(m, k) также следующим образом. Сначала покрасим одну точку в синий цвет m способами. Теперь нам нужно покрасить в красный цвет k точек, выбранных из линейного массива m -1 точек так, чтобы среди них не было двух последовательных. Одним из способов дальнейших рассуждений может быть следующий. Расположим m - 1 - k неокрашенных точек в линию и вставим k красных точек в m - k промежутков между неокрашенными точками (считая начало и конец) . Это можно сделать
Предложенное доказательство основано на некотором общем принципе перехода от кругового к линейному массиву. Этот принцип широко используется при решении комбинаторных задач. Второе доказательство. Пометим точки числами 1, 2, ... , m в возрастающем по часовой стрелке порядке. Мы хотим покрасить k из них в красный цвет, так чтобы не было двух последовательных красных точек. Сначала подсчитаем число возможностей, при которых точка 1 не окрашена в красный цвет. Расположим m- k неокрашенных точек по кругу, пометив одну из них единицей и вставим k красных точек в m - k промежутков между неокрашенными точками Следовательно,
На основании доказанной леммы имеем Утверждение 1.19. Многочлен Nn(x) для доски B={(i, i), (i, i+1(mod n)): 1 £ i £ n} дается формулой
В частности, число N0перестановок pÎsn , для которых p(i)¹i, i+1(mod n) при 1 £ i £ n, дается формулой

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
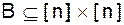 . Множество B называют доской. Для pÎsn определим график G(p) перестановки p условием
. Множество B называют доской. Для pÎsn определим график G(p) перестановки p условием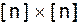 . Тогда Njесть число способов размещения n не атакующих друг друга ладей на доске
. Тогда Njесть число способов размещения n не атакующих друг друга ладей на доске 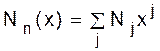 .
. . (1.29)
. (1.29)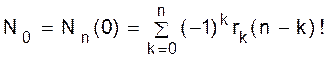 . (1.30)
. (1.30) способами. Следовательно,
способами. Следовательно, 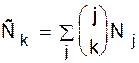 . С другой стороны, можно было бы сначала выбрать rk способами множество C, а затем расширить его (n - k)! способами до перестановки p. Следовательно, Ck= rk(n - k)!. Поэтому
. С другой стороны, можно было бы сначала выбрать rk способами множество C, а затем расширить его (n - k)! способами до перестановки p. Следовательно, Ck= rk(n - k)!. Поэтому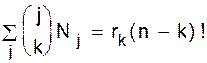 ,
,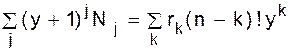 .
.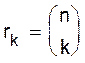 , так что
, так что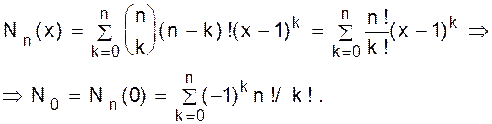
 .
. способами. Следовательно,
способами. Следовательно,  . Откуда
. Откуда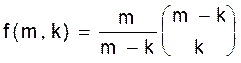 .
.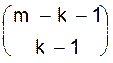 способами k - 1 красную точку на m - k - 1 разрешенных мест.
способами k - 1 красную точку на m - k - 1 разрешенных мест.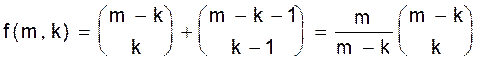 . ð
. ð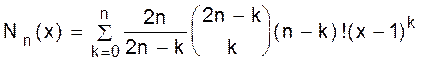 .
.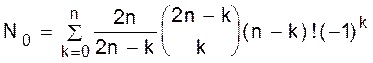 . ð
. ð