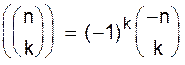|
|
Биномиальные коэффициентыCвое название биномиальные коэффициенты получили от соответствующей им производящей функции, являющейся степенью бинома:
Для доказательства справедливости написанного соотношения (1.1) достаточно заметить, что коэффициент при xk равен числу способов, которыми из mсомножителей (1+x) ... (1+x)можно выбрать k сомножителей. Отметим некоторые важнейшие соотношения для биномиальных коэффициентов (чисел сочетаний). 1.
Это важнейшее соотношение - прямое следствие того факта, что каждому k-элементному подмножеству Y 2.
Зафиксируем некоторый элемент x из n- элементного множества X. Множество T всех k - элементных подмножеств множества X распадается на два непересекающихся класса:
класс T1 подмножеств, которые не содержат элемент x, и класс T2подмножеств, которые его содержат. Мощность первого класса составляет Продемонстрируем эффективность использования производящей функции биномиальных коэффициентов для получения комбинаторных соотношений, включающих число сочетаний. 3. Полагая в (1.1) x=1 получим
Эта формула следует и из того, что сумма слева есть число всех подмножеств n-элементного множества. 4.
Дифференцируя (1.1) и полагая x=1, получаем соотношение (1.4) . 5.
Равенство легко следует из следующего равенства для производящих функций: (1+x)m+n =(1+x)m (1+x)n . Полагая в (1.5) m = k = n, получим
Отметим, что задача прямого доказательства последнего равенства без использования производящей функции достаточно трудна. 6. Полагая в (1.1) x = –1, получаем
Отсюда следует, что
где через Исчисление конечных разностей Приведем пример использования биномиальных коэффициентов в вычислительной математике. Пусть дана функция j, определенная на множестве действительных (возможно целых) чисел и принимающая действительные значения. Определим новую функцию Dj(x), называемую первой разностью j, формулой
Оператор D называется разностным оператором первого порядка; кратко и очень упрощенно можно определить исчисление конечных разностей как исследование оператора D . Можно применить оператор D k раз и получить k-ый разностный оператор
Число Dkj(x) называется k-ой разностью j в точке x (Dkj(0) называется k-ой разностью j в 0). Определим другой оператор E, называемый оператором сдвига, формулой
Таким образом, D=E - I, где I означает единичный оператор:
Тогда первая разность функции может быть записана в виде:
Разности более высоких порядков определяются рекуррентным соотношением
Откуда получаем выражение для n -ой разности:
В частности,
что дает явную формулу для k-ой разности в терминах значений j(0), j(1), ... , j(k). Нетрудно обратить формулу (1.6) и выразить j(n) через Di j(0). Именно,
Напишем теперь в строку значения ... j(-2) j(-1) j(0) j(1) j(2) j(3)... Если внизу написать между каждой парой последовательных членов j(i), j(i +1) их разность j(i +1) - j(i) = Dj(i), то получим последовательность ...Dj(-2) Dj(-1) Dj(0) Dj(1) Dj(2) ... . Повторение этой процедуры приводит к таблице разностей функции j, k-ая строка которой состоит из значений Dkj(n). Диагональ, начинающаяся в j(0) и идущая направо вниз, состоит из разностей Dkj(0) в 0. Например, пусть j(n) = n4 . Таблица разностей (начинающаяся с j(0) ) выглядит так:
Из формулы (1.7) следует, что
В этом случае, так как n4-многочлен четвертой степени и Предыдущее рассуждение, конечно, не относится лишь к функции n4 . Подобные рассуждения приводят к следующим результатам. 1. Функция j - полином степени, не превосходящей d, тогда и только тогда. когда Dd+1j(n) =0 (или Ddj(n) - постоянная). 2. Если многочлен j(n) степени, не превосходящей d, разложен в ряд по базису
Еще одна связь комбинаторных объектов с исчислением конечных разностей дается формулой (1.15). Разложения Существует тесная связь между подмножествами множеств и разложениями целого числа. Определение. Разложение n есть представление числа n в виде упорядоченной суммы положительных целых. Например, существует восемь разложений числа 4, а именно: 1+1+1+1 3+1 2+1+1 1+3 1+2+1 2+2 1+1+2 4 Если разложение s содержит в точности k слагаемых, то говорят, что s имеет k частей и называется k -разложением. Если a1+ a2+...+ ak - k -разложение s числа n, определим (k -1) - элементное подмножество q(s) (или (k -1)- подмножество ) множества {1, 2, ..., n-1} формулой q(s) ={a1, a1+a2, ... , a1 + a2+ ... + ak-1} . Эта формула устанавливает взаимно однозначное соответствие (биекцию) между всеми k-разложениями и (k -1)- подмножествами q(s) множества {1, 2, ..., n-1}. Следовательно, существует · ½ · ·½ ·½·½· · ·½· · соответствуют разложению 1+2+1+1+3+2 . Другая проблема, тесно связанная с разложениями, есть задача подсчета числа N(n, k) решений уравнения x1 + x2+... +xk = n в неотрицательных целых числах. Решение такого уравнения называется слабым разложением n на k частей, или слабым k- разложением числа n. (Решение в положительных целых числах есть просто k-разложение n.) Если мы положим y1 = x1+1, y2= x2+1, ... , yk=xk+1, то получим, что N(n, k) есть количество решений в положительных числах уравнения y1 + y2+... +yk = n +k , то есть число k-разложений числа n+k . Таким образом, Подобным же приемом (найти его предоставляется читателю) доказывается, что число решений неравенства x1 + x2+... +xk £ n в неотрицательных целых числах есть k - подмножество T n - множества S иногда называют k - сочетанием из S без повторений. Так возникает задача подсчета числа k - сочетаний из S с повторениями; то есть мы выбираем k элементов из множества S, не взирая на их порядок и допуская повторяющиеся элементы. Обозначим число таких способов Если S = {y1 , ... , yn} и мы положим xi= n(yi), то увидим, что
Прямое комбинаторное доказательство утверждения (1.9) таково. Пусть {a1, a2, ... , ak}, 1 £ a1< a2 < ... < ak £ n + k - 1, есть k -подмножество множества [ n + k - 1]= {1, 2, ... , n+k - 1}. Положим bi = ai - i + 1. Тогда {b1 , b2 , ... , bn} - k -мультимножество на множестве [n]. Обратно, если дано k - мультимножество 1 £ b1 £ b2£ bk£ n на [n], то определив ai формулой ai = bi + i - 1, видим, что {a1 , a2 , ..., ak } есть k -подмножество множества [n + k - 1] . Следовательно, мы определили взаимно однозначное соответствие между Поучителен подход к мультимножествам с точки зрения производящих функций. Cовершенно аналогично проведенному исследованию подмножеств множества S = {x1 , x2 , ... , xn } имеем
Положим xi = x. Тогда
Но
так что
Появление элегантной формулы
не случайно. Это простейший пример комбинаторной теории взаимности. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
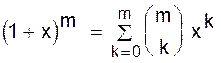 (1.1)
(1.1) (1.2)
(1.2) X однозначно соответствует (n-k) - элементное подмножество X\Y множества X.
X однозначно соответствует (n-k) - элементное подмножество X\Y множества X. (1.3)
(1.3) ,
, , а второго
, а второго 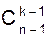 , то есть столько, сколько имеется (k-1) - элементных подмножеств множества X\{x}. ð
, то есть столько, сколько имеется (k-1) - элементных подмножеств множества X\{x}. ð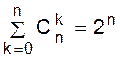
 (1.4)
(1.4) (1.5)
(1.5)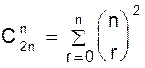 .
. .
. ,
, обозначена целая часть числа m/2. ð
обозначена целая часть числа m/2. ð .
. .
. .
. .
. .
.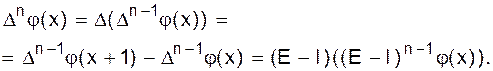
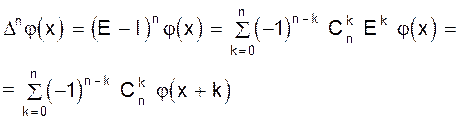
 , (1.6)
, (1.6) . (1.7)
. (1.7) (1.8)
(1.8)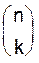 при фиксированном k есть многочлен степени k, написанное выше разложение обрывается после члена
при фиксированном k есть многочлен степени k, написанное выше разложение обрывается после члена  , то есть Dk04 = 0, если k > 4 (или, более общим образом, Dk n4 = 0, если k > 4).
, то есть Dk04 = 0, если k > 4 (или, более общим образом, Dk n4 = 0, если k > 4). . ð
. ð k -разложений n и 2n - 1 разложений n. Разложение часто схематично представляют, рисуя в строку n точек и k - 1 разделяющую вертикальную черту. Точки разделяются по k линейно упорядоченным “отделениям”, числа точек в отделениях дают k -разложение числа n . Например, последовательность
k -разложений n и 2n - 1 разложений n. Разложение часто схематично представляют, рисуя в строку n точек и k - 1 разделяющую вертикальную черту. Точки разделяются по k линейно упорядоченным “отделениям”, числа точек в отделениях дают k -разложение числа n . Например, последовательность .
. .
.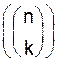 . Например,
. Например,  . Если S = {1,2,3}, то подходящие сочетания есть 11, 22, 33, 12, 13, и 23. Эквивалентное, но более точное определение и исследование сочетаний с повторениями может быть проведено, если ввести понятие мультимножества. На интуитивном уровне мультимножество есть множество с повторяющимися элементами, например {1, 1, 2, 5, 5}. Более точно, конечное мультимножество M на множестве S есть функция n: S®À(À - множество натуральных чисел), такая, что
. Если S = {1,2,3}, то подходящие сочетания есть 11, 22, 33, 12, 13, и 23. Эквивалентное, но более точное определение и исследование сочетаний с повторениями может быть проведено, если ввести понятие мультимножества. На интуитивном уровне мультимножество есть множество с повторяющимися элементами, например {1, 1, 2, 5, 5}. Более точно, конечное мультимножество M на множестве S есть функция n: S®À(À - множество натуральных чисел), такая, что  ; n(x) рассматривается как число повторений элемента x. Целое число
; n(x) рассматривается как число повторений элемента x. Целое число  называют мощностью или числом элементов M и обозначают êM ê. Если S = {x1 , x2 ,
называют мощностью или числом элементов M и обозначают êM ê. Если S = {x1 , x2 , . Множество всех k - мультимножеств на S обозначается символом
. Множество всех k - мультимножеств на S обозначается символом  .
. . (1.9)
. (1.9) и
и  , что и требовалось доказать.
, что и требовалось доказать.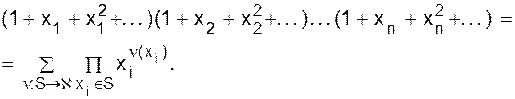
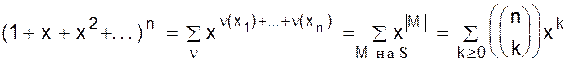 .
.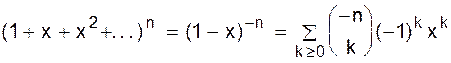 ,
, .
.