
|
|
Циклическая структура перестановокПерестановки множеств и мультимножеств - один из самых богатых объектов перечислительной комбинаторики. Основная причина этого - большое разнообразие способов комбинаторного представления перестановки. Перестановку можно представлять как слово или как функцию. В частности, функция Если рассматривать перестановку p конечного множества S как взаимно однозначное отображение p: S ® S, то естественно для каждого xÎS рассмотреть последовательность x, p(x), p2(x), ... . В конце концов (так как p - взаимно однозначное соответствие, и множество S предполагается конечным) мы вновь получим x. Таким образом, для некоторого единственного наименьшего k ³ 1 имеем, что pk(x) = x и элементы x, p(x), ... , p k-1(x) все различны. Назовем последовательность (x, p(x), ... , p k-1(x)) циклом перестановки p длины k. Циклы (x, p(x), ... , p k-1(x)) и (p i(x), p i+1(x), ... , p k-1(x), x, ... , · в каждом цикле пишется первым его наибольший элемент; · циклы записываются в порядке возрастания их максимальных элементов. Пусть c(n, k) - число таких перестановок множества из n элементов, которые имеют k циклов. Будем обозначать множество всех перестановок n - элементного множества символом sn. Утверждение 1.4. Числа c(n,k) удовлетворяют следующему рекуррентному сотношению: c(n, k) = (n - 1) c(n-1, k) + c(n-1, k-1) , n, k ³1, с начальными условиями c(n, k) = 0 при n £ 0 или k £ 0, за исключением Докажем сфомулированное утверждение. Возьмем перестановку p Î sn-1с k циклами. Мы можем вставить символ n после любого из символов 1, 2, ... , n-1 в разложении перестановки p на непересекающиеся циклы n-1 способом, получив таким образом разложение на непересекающиеся циклы перестановки p¢Îsnс k циклами, где n встречается в цикле длины, не меньшей 2. Следовательно, существует (n-1)×c(n-1,k) перестановок p¢Îsnc k циклами, для которых p¢(n)¹n. С другой стороны, если выбрана перестановка p¢Îsn-1с k-1 циклом, ее можно достроить до перестановки p¢Îsnс k циклами, удовлетворяющей условию p¢(n) = n. Положим
Следовательно, имеется c(n - 1, k - 1) перестановок p¢Îsnс k циклами, для которых p¢(n) = n, и доказательство закончено. ð Числа c(n,k) = ( - 1)n-ks(n,k) известны под названием чисел Стирлинга первого рода без знака. Укажем на еще одну важную роль чисел c(n, k). Пусть x - переменная. Фиксируем n ³ 0. Тогда имеет место Утверждение 1.5.
Доказательство. Положим
Отсюда следует, что b(n, k) = (n - 1)b(n - 1, k) + b(n - 1, k - 1). Поэтому b(n, k) удовлетворяют тем же рекуррентным соотношениям и начальным условиям, что и c(n, k), а значит, они совпадают. ð Упорядоченные размещения. Пусть x - переменная или действительное число. Положим, по определению, [x]n = x(x + 1)(x + 2) ××× (x + n - 1). Обозначение [x]nчитается как “n факториал от x вверх” или “верхняя n-ая степень x”. Определение. Пусть X - множество из n объектов 1,2,...,n, которые должны быть размещены по m ящикам так, чтобы каждый ящик содержал бы последовательность, а не множество, как прежде, помещенных в нем объектов. Два размещения совпадают (равны), если в каждом ящике содержится одна и та же последовательность объектов. Размещения такого типа называются упорядоченными размещениями n объектов по m ящикам. ð Приведем для примера всевозможные упорядоченные размещения двух объектов 1 и 2 в двух ящиках. Ящики будем изображать в виде последовательности вертикальных черточек ½, представляющих разделяющие ящики перегородки. Таким образом 2½1 представляет размещение, при котором в первом ящике находится элемент 2, а во втором ящике - элемент 1. Таблица всевозможных размещений двух объектов в двух ящиках имеет следующий вид: ƽ1 2 ; 1½2 ; 1 2½Æ ; ƽ2 1 ; 2½1 ; 2 1½Æ . Утверждение 1.6. Число упорядоченных размещений n объектов по m ящикам равно [m]n = m(m + 1)... (m + n - 1) (полагаем [m]o = 1). Доказательство. Построим сначала таблицу Tn-1всех упорядоченных размещений объектов 1,2,...,n-1 по m ящикам. Каждое размещение i1 i2...| ik ik+1 ...| ...|...|... in-1 можно представить как последовательность (n-1) + (m-1) символов, являющихся либо буквой i j , либо вертикальной чертой |. Чтобы из этой последовательности получить последовательность, представляющую упорядоченное размещение n объектов в нее достаточно всеми возможными способами добавить символ n. Символ n можно добавить к этой последовательности (n-1) + Таким образом | Tn | =(m+n-1) |Tn-1| = (m+n-1)(m+n-2) ... (m+1) |T1| = [m]n. Очевидно, что |T1| = 1. ð Отметим простые, часто используемые соотношения: [m]n= (m-n+1) [m]n-1 ; [m]n =(m+n-1) [m]n-1 ; [m]n = m! / (m-n)! ; [m]n =(m+n-1)! / (m-1)! ; [m]n = [m+n-1]n ; [m]n = [m]n-1(m+n-1).
Определение. Пусть A - алфавит (то есть конечное множество символов) со множеством букв a1, ... ,am , упорядоченных так, что a1 < a2 < ...< am. Cлово x1 x2 ... xn длины n - монотонное, если x1 Пример. Пусть A={a,b,c,d}, a < b < c < d. Тогда монотонными будут, например, следующие слова: aaa, aab , abc, aad, bcd, ddd . (По несколько устаревшей терминологии, это комбинации с повторениями из m объектов, взятые по n штук). Утверждение 1.7.Число монотонных слов длины n в алфавите из m букв равно [m] n/n! . Доказательство. Рассмотрим упорядоченное размещение n объектов 1,2 ,..., n по m ящикам a1 , ... , am и пусть ему соответствует монотонное слово следующим образом:
В соответствующем слове буква a1написана столько раз, сколько объектов в ящике a1, затем буква a2столько раз, сколько объектов в ящике a2, ... . Каждому упорядоченному размещению n объектов соответствует единственное монотонное слово. Все монотонные слова таким образом могут быть получены. Монотонному слову, с другой стороны, соответствует ровно n! различных упорядоченных размещений. Поэтому число монотонных слов есть [m]n/n! . ð Приложение. (Задача Муавра). Найдем число способов представления целого положительного числа m как упорядоченной суммы n неотрицательных целых чисел m = u 1 + ...+ u n. Два таких представления m=u1 + ...+ un и m=u1¢ + ...+ un¢ будем считать совпадающими тогда и только тогда, когда u1= u1¢ , ... , un= un¢ , то есть когда совпадают слагаемые и порядок их следования. Положим значение skравным частичной сумме первых k членов последовательности n1, ... , nk: sk= n1 + n2 + ... + nk . Каждому представлению m в виде суммы n слагаемых взаимно однозначно соответствует слово Число представлений равно:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , то есть p(1) = 4, p(2) = 2, p(3) = 7, p(4) = 1, p(5) = 3, p(6) = 6, p(7) = 5, то p = (14)(2)(375)(6). Конечно, возможны различные обозначения такого представления перестановки; например, имеем: p = (753) (14) (6) (2). Можно определить стандартное представление:
, то есть p(1) = 4, p(2) = 2, p(3) = 7, p(4) = 1, p(5) = 3, p(6) = 6, p(7) = 5, то p = (14)(2)(375)(6). Конечно, возможны различные обозначения такого представления перестановки; например, имеем: p = (753) (14) (6) (2). Можно определить стандартное представление: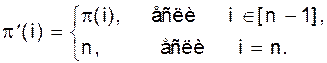
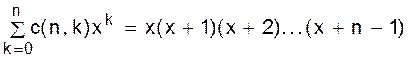

 x2
x2 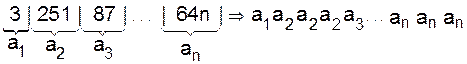 .
.