
|
|
Представление о результатах ПостаВесьма глубокое изучение замкнутых классов в Р2было осуществлено американским математиком Э. Постом в 1921 - 1941 годах. Им была описана структура всех замкнутых классов в Р2. Сформулируем некоторые из важнейших результатов этих исследований. Определение. Система функций { f1, f2, ... , fn, ...} из замкнутого класса К называется полной в К, если ее замыкание совпадает с К. ð Иначе говоря, система полна в К, если каждая функция из К может быть выражена в виде формулы через функции данной системы. Определение.Система функций { f1, f2, ... , f n, ...} из замкнутого класса К называется его базисом , если она полна в К, но всякая ее собственная подсистема не является полной в К.ð Так, система f1 = x1x2, f2= 0 , f3= 1, f4= x1+x2является базисом в Р2. Можно показать, что система функций {0, 1, x1x2, x1 Ú x2} является базисом для класса М монотонных функций. Теорема 2.12. Каждый замкнутый класс из Р2имеет конечный базис. Теорема 2.13. Мощность множества замкнутых классов в Р2счетная. Хотя вторая из приведенных теорем логически вытекает из первой, однако в доказательствах Поста сначала устанавливается второй факт, а затем - первый. Элементы теории графов Начало теории графов как математической дисциплине было положено Эйлером в его знаменитом рассуждении о Кёнигсбергских мостах. Однако эта статья Эйлера 1736 года была единственной на эту тему в течение почти ста лет. Естественные науки оказали свое влияние на развитие теории графов благодаря исследованиям электрических сетей, моделей кристаллов и структур молекул. Развитие формальной логики привело к изучению бинарных отношений в форме графов. Большое число популярных головоломок поддавалось формулировке непосредственно в терминах графов, и это приводило к пониманию, что многие задачи такого рода содержат некоторое математическое ядро, важность которого выходит за рамки конкретного вопроса. Наиболее знаменитая из этих задач - проблема четырех красок, впервые поставленная перед математиками Де Морганом около 1850 г. Никакая другая проблема не вызывала столь многочисленных и остроумных работ в области теории графов. Благодаря своей простой формулировке и раздражающей неуловимости она до 1973 г. оставалась мощным стимулом исследований различных свойств графов (предложенное в 1973 году положительное решение этой проблемы до сих пор оспаривается некоторыми математиками). Настоящее столетие было свидетелем неуклонного развития теории графов, которая за последние двадцать лет вступила в новый период интенсивных разработок. В этом процессе явно заметно влияние запросов новых областей приложений: теории игр, программирования, оптимизации, теории передачи сообщений, электрических и контактных сетей, а также проблем биологии и психологии. Предметом первых задач в теории графов были конфигурации, состоящие из точек и соединяющих их линий. В этих рассмотрениях было несущественно, прямые ли это линии или же они являются криволинейными непрерывными дугами, соединяющими концевые точки, где расположены эти линии, являются ли они длинными или короткими. Существенно лишь то, что они соединяют две данные точки. Это приводит в определению графа как абстрактного математического понятия. Граф G = <V, Е> есть совокупность множества вершин V и множества ребер (дуг) Е , причем Граф неориентированный, если все его ребра не ориентированы, и граф ориентированный, если все его ребра ориентированы. Ребро ориентированного графа мы обозначаем символом <x, y>; ребро неориентированного графа обозначается символом {x, y}. В случае, когда несущественно, о каком ребре идет речь, или когда это ясно из контекста, будем произвольное ребро графа обозначать символом (x, y). В приложениях граф обычно интерпретируется как совокупность точек V, в которой точки x и y соединены дугой со стрелкой если <x, y>ÎE и дугой без стрелки если При фактическом изображении графа имеется большая свобода в размещении вершин и в выборе формы соединяющих их дуг. Поэтому может оказаться, что один и тот же граф представляется совершенно различными чертежами. Будем говорить, что два графа G = <V, E> и G¢ = <V¢, E¢> изоморфны, если существует такое взаимно-однозначное соответствие между множествами их вершин V и V¢, что вершины соединены ребрами в одном графе тогда и только тогда, когда соответствующие им вершины соединены в другом графе. Таким образом, если VÛV¢и при этом соответствии x Û x¢, yÛy¢, то Задача. Доказать, что графы, изображенные на следующем рисунке 3.1, изоморфны.
Рис. 3.1. Вершина, не инцидентная никакому ребру, называется изолированной. При определении множества вершин V данного графа часто имеет смысл учитывать только неизолированные вершины. Важным случаем является неориентированный полный граф U = U(V), ребрами которого являются всевозможные пары {x,y} для всех различных вершин x и y из V. В ориентированном полном графе Сформулированное определение графа, вместе с соответствующим изображением, достаточно для многих задач. Однако, для некоторых целей желательно понятие графа несколько расширить. 1. Можно допускать рёбра, у которых обе вершины совпадают l =(x,x). Такое ребро называется петлей. U0 - полный граф с петлями. 2. Пара вершин может соединяться несколькими ребрами ei= (x,y)i, в частности вершины x и y могут соединяться несколькими ребрами в каждом направлении. Степени вершин Граф называется конечным, если число его ребер конечно. При таком определении конечный граф может иметь бесконечное число вершин, но все они, кроме конечного числа, изолированные. Пусть G - неориентированный граф. Числоr(x)ребер, инцидентных вершине x,называется локальной степенью, или просто степенью вершины x графа G. В каждом случае должно быть указано, считается петля однократной или двойной. Пусть r(a, b) = r(b, a) - число ребер, соединяющих вершины a и b. Очевидно, каждая степень каждой вершины есть сумма кратностей в вершине a:
Обозначим через ne = ne (G) число ребер в неориентированном графе G. Так как каждое ребро учитывается в двух степенях в вершинах a и b, то
Отсюда следует Теорема 3.1. 1В конечном графе число вершин нечетной степени четно. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 есть множество упорядоченных пар <x,y> для ориентированного графа и
есть множество упорядоченных пар <x,y> для ориентированного графа и 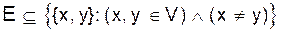 для неориентированного графа ( при этом для неориентированного графа считаем, что ребра {a, b} и {b, a} совпадают {a, b}={b, a}).
для неориентированного графа ( при этом для неориентированного графа считаем, что ребра {a, b} и {b, a} совпадают {a, b}={b, a}).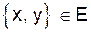 . В случае ориентированного графа для ребра
. В случае ориентированного графа для ребра 
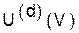 имеются пары ребер <x,y> и <y,x> для всех различных вершин x, y Î V.
имеются пары ребер <x,y> и <y,x> для всех различных вершин x, y Î V.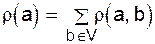 .
.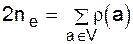 . Формула остается справедливой и при наличии петель, если только в локальных степенях вершин считать их дважды. Поэтому
. Формула остается справедливой и при наличии петель, если только в локальных степенях вершин считать их дважды. Поэтому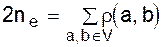 .
.