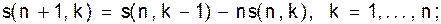|
|
Числа Стирлинга первого родаЭлементы комбинаторики. Введение Сейчас трудно было бы, пожалуй, назвать раздел теоретической информатики, в котором в течение последнего десятилетия были бы достигнуты большие успехи, нежели в конструировании и анализе комбинаторных алгоритмов - важнейшей проблемы комбинаторики. С одной стороны, было обнаружено много новых, более эффективных методов решения комбинаторных задач с помощью ЭВМ, с другой стороны - получены теоретические результаты, свидетельствующие все более явно о том, что для широкого класса проблем не существует достаточно эффективных алгоритмов. Эффективные комбинаторные алгоритмы находят применение во многих областях нечисленной обработки информации, особенно в дискретной оптимизации и в исследовании операций, в вычислительной математике. Количество комбинаторных задач и их разнообразие быстро растет. К их решению прямо или косвенно приводят многие практические задачи. Во многих областях математики (теория графов, теория чисел, теория групп, кибернетика, вычислительная математика) имеются задачи или группы задач, комбинаторный характер которых угадывается без усилий. Между этими задачами часто можно установить сеть взаимных интерпретаций, что приводит к мысли о наличии их общей теоретической основы. При этом оказывается, что несмотря на заманчивую простоту постановки, комбинаторные задачи в большинстве очень трудны. Комбинаторика - раздел математики, в котором изучаются вопросы о том, сколько различных конфигураций (комбинаций), подчиненных тем или иным условиям, можно составить из заданных объектов. Основная проблема комбинаторики - подсчет числа элементов в конечном множестве. В этой широкой проблеме можно условно выделить следующие основные направления исследований: * Изучение известных конфигураций. * Исследование неизвестных конфигураций. * Подсчет числа конфигураций. * Приближенный подсчет числа конфигураций. * Перечисление конфигураций. * Оптимизация. Два принципа комбинаторики При подсчете числа различных комбинаций в комбинаторике используются следующие два основных правила. Правило произведения. Если объект A может быть выбран m различными способами и после каждого из таких выборов объект B в свою очередь может быть выбран n различными способами, то выбор двух объектов “A и B” в указанном порядке может быть осуществлен m×n способами. Правило суммы. Если объект A может быть выбран m различными способами, а объект B может быть выбран другими n различными способами при условии, что одновременный выбор A и B невозможен, то выбор “A или B” может быть осуществлен m + n способами. Функции и размещения Классической задачей комбинаторики является задача определения числа способов размещения некоторых объектов в каком-то количестве ящиков так, чтобы были выполнены заданные ограничения. Эту задачу можно сформулировать несколько более формально следующим образом. Термины “функция”, “отображение”, “преобразование” и “соответствие” будут в дальнейшем использоваться как синонимы. При этом запись Пусть даны множества X, Y, причем множество X содержит n элементов (|X| = n), а множество Y содержит m элементов (|Y| = m). В этих терминах задача может быть сформулирована следующим образом: сколько существует функций (отображений) Другую традиционную интерпретацию можно получить, трактуя Y как множество цветов, а f(x) как “цвет объекта x”. Наша задача эквивалентна, таким образом, вопросу, сколькими способами можно покрасить объекты так, чтобы были соблюдены некоторые ограничения. Наконец, каждому отображению f : X®Y, ½X½ = n, ½Y½=m, можно взаимно однозначно сопоставить слово< f(x1), ... , f (xn)> = <y1, y2, ... , yn> = Самой простой является задача, в которой на рассматриваемые функции не накладывается никаких ограничений. Утверждение 1.1. Если |X| = n, |Y| = m, то количество всех функций Эквивалентное утверждение 1.1¢. Число слов длины n в алфавите из m символов равно mn. Доказательство. Без потери общности можно всегда считать, что X = {1,..., n}, Y = {1,..., m}. Каждую функцию можно тогда отождествить с последовательностью < f(1),..., f (n)> = < y1 ,...,yn> . Каждый член yiпоследовательности можно выбрать m способами, что дает mn возможностей выбора последовательности <y1 ,...,yn>. Определения. Отображение j: X ® Y сюръективно, если для каждого элемента yÎY существует хотя бы один элемент xÎX , такой что j(x)=y (в каждом ящике при размещении находится хотя бы один объект, все буквы алфавита используются в слове, все цвета используются при окраске). Отображение j: X В перечисленных интерпретациях основной задачи сюръективному отображению соответствуют такие размещения объектов по ящикам, что каждый ящик не пуст; раскраски объектов такие, что все цвета использованы при раскраске; слова в заданном алфавите, такие что в каждом слове использованы все буквы алфавита. Инъективному отображению соответствуют такие размещения объектов по ящикам, в которых каждый ящик содержит не более одного объекта; такие раскраски объектов, при которых цвета всех объектов различны и, наконец, слова в алфавите, все буквы которых различны. Если x - действительное число, положим по определению [x]n= x (x-1)(x-2)...(x-n+1). Обозначение [x]nчитается как “n факториал от x вниз” или “нижняя n-ая степень x”. Утверждение 1.2.Число инъективных отображений (инъекций) множества X из n элементов, | X| = n, во множество Y из m элементов, |Y|= m, есть [m]n. Эквивалентное утверждение 1.2¢. Число слов длины n без повторений букв в алфавите из m букв есть [m]n. Доказательство. Будем определять на этот раз число инъективных, (то есть имеющих все различные члены) последовательностей <y1,...,yn>. Элемент y1 может быть выбран m способами, элемент y2можно выбрать m-1 способом из оставшихся элементов. В общем случае, если уже выбраны элементы y1,...,yi-1, то в качестве yiможет быть выбран любой из m-i +1 элементов множества Y\{y1,...,yi-1}. (Принимаем, что m Отметим, что
Определение. Каждое взаимно однозначное отображение f :X®X называется перестановкой множества x. ð В соответствии с утверждением1.2 число перестановок n- элементного множества равно n!. Числа Стирлинга первого рода Выражение [x]nявляется полиномом степени n от переменной x, следовательно его можно представить в виде следующего разложения по степеням x: [x]n = s(n,0) + s(n,1)x +...+ s(n,n)xn . По определению, коэффициенты s(n,k) такого разложения называются числами Стирлинга первого рода. Утверждение 1.3.Числа Стирлинга первого рода удовлетворяют следующим рекуррентным соотношениям:
s(n, 0)= 0; s(n, n)= 1. Доказательство. По определению [x]n+1 = [x]n(x-n). Представляя полиномы в левой и правой частях равенства в виде разложения по степеням x, получим s(n+1,n+1)xn+1 + ××× + s(n+1, k)xk + ×××+s(n+1,0)= (s(n,n)+ ××× +s(n, k-1)xk-1 + s(n,k)xk + ××× +s(n,0))(x-n). Вычисляя и приравнивая коэффициенты при xk слева и справа, получаем первую формулу утверждения. Другие две формулы очевидны. ð Утверждение 1.3дает эффективный способ рекуррентного вычисления чисел Стирлинга первого рода. Приведем часть значений таблицы s(n,k) для начальных значений n и k :
Отметим связь чисел Стирлинга первого рода, в частности рекуррентного соотношения для них, с изучением циклической структуры перестановок. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , удовлетворяющих заданным ограничениям. Элементы множества X соответствуют объектам, элементы множества Y- ящикам, а каждая функция f : X® Y определяет некоторое размещение, указывая для каждого объекта xÎX ящик y = f(x) Î Y, в котором данный объект находится.
, удовлетворяющих заданным ограничениям. Элементы множества X соответствуют объектам, элементы множества Y- ящикам, а каждая функция f : X® Y определяет некоторое размещение, указывая для каждого объекта xÎX ящик y = f(x) Î Y, в котором данный объект находится.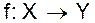 равно mn.
равно mn.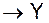 инъективноесли
инъективноесли 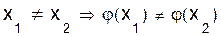 . ð
. ð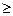 n, если n>m, то и [m]nи искомое число функций равно 0). Это дает m(m-1)...(m - n+1) возможность выбора инъективных последовательностей <y1,...,yn>. ð
n, если n>m, то и [m]nи искомое число функций равно 0). Это дает m(m-1)...(m - n+1) возможность выбора инъективных последовательностей <y1,...,yn>. ð