
|
|
О машинном представлении графов.Очевидно, что наиболее понятный и полезный для человека способ представления графа - изображение графа на плоскости в виде точек и соединяющих их линий - будет совершенно бесполезным, если мы хотим решать с помощью ЭВМ задачи, связанные с графами. Выбор соответствующей структуры данных для представления графов оказывает принципиальное влияние на эффективность алгоритмов. В теории графов классическим способом представления графа служит матрица инциденций. Для графа G=<V, E> - это матрица I(G) с n строками, соответствующими вершинам, |V| = n,и с mстолбцами, |E| = m, соответствующими ребрам. Для ориентированного графа столбец, соответствующий ребру < x, y > содержит -1 в строке, соответствующей вершине x, 1 в строке, соответствующей вершине y, и нули во всех остальных строках (петлю Пример.
Рис. 3.2. Для ориентированного графа, изображенного на рис. 3.2, матрица инциденций имеет вид:
<1,2> <1,3> <3,2> <3,4> <4,3>
С алгоритмической точки зрения матрица инциденций является, вероятно, самым худшим способом представления графа, который только можно представить. Во-первых, он требует m´nячеек памяти. Доступ неудобен. Ответ на элементарные вопросы типа “существует ли ребро <x,y>?”, “к каким вершинам ведут ребра из x?”, требует перебора всех столбцов матрицы. Более удобным способом представление графа является матрица смежности (вершин), определяемая как матрица B = || bi j|| размера n´n, где bi j= 1, если существует ребро, ведущее из вершины x в вершину y, bij= 0 в противном случае. Здесь мы подразумеваем, что ребро {x, y} неориентированного графа идет как от x к y, так и от y к x, так что матрица смежности такого графа всегда является симметричной. Ответ на вопрос типа “{x,y} Недостаток такого способа представления графа - n´n ячеек занятой памяти независимо от числа ребер. Более экономным в отношении требуемого объема памяти (особенно для неплотных графов m << n´n) является метод представления графа с помощью списка пар. Пара (x, y)соответствует ребру <x, y>,если граф ориентированный, и ребру {x, y},если граф неориентированный. Очевидно, что объем памяти в этом случае составляет 2mячеек. Неудобство - большое число шагов, порядка m в худшем случае, необходимое для получения множества вершин, к которым ведут ребра из данной вершины. Для приведенного на рис. 3.2.графа список пар имеет следующий вид: (1, 2), (3, 2), (4, 3), (1,3), (3, 4) . Ситуацию можно значительно улучшить, упорядочив множество пар лексикографически и применяя двоичный поиск, но лучшим решением во многих случаях оказывается структура данных, которая называется списками инцидентности. Она содержит для каждой вершины vÎV список вершин u, таких что
Каждый элемент списка инцидентности имеет вид где
Поиск в графе Будем далее рассматривать ориентированные и неориентированные графы без петель и кратных ребер, которые будем называть простыми. Существует много алгоритмов на графах, в основе которых лежит систематический перебор вершин графа, такой, что каждая вершина просматривается в точности один раз. Поэтому важной задачей является нахождение хороших методов поиска в графе. Вообще говоря, метод поиска ”хороший”, если 1) он позволяет легко применить этот метод в алгоритме решения задачи (“погрузить” алгоритм решения нашей задачи в этот метод); 2) каждое ребро графа анализируется не более одного раза (или, что существенно не меняет ситуации, число раз, ограниченное константой). Опишем теперь такой метод поиска в неориентированном простом графе, который стал одним из основных методов проектирования графовых алгоритмов. Этот метод называется методом поиска в глубину, по причинам, которые вскоре станут ясными. Поиск в глубину в графе Общая идея этого метода состоит в следующем. Мы начинаем поиск с некоторой фиксированной вершины v0. Затем выбираем произвольную вершину u, смежную с v0( (v0, u)ÎЕ), и повторяем процесс от u. В общем случае предположим, что мы находимся в вершине v. Если существует новая (еще непросмотренная) вершина u, (v, u)ÎЕ, то мы рассматриваем эту вершину (она перестает быть новой) и, начиная с нее, продолжаем поиск. Если же не существует ни одной новой вершины, смежной с v, то мы говорим. что вершина v использована, возвращаемся в вершину, из которой мы попали в v, и продолжаем процесс (если v = v0, то поиск закончен). Таким образом, поиск в глубину из вершины v основывается на поиске в глубину из всех новых вершин, смежных с v. Этот процесс поиска из вершины v для неориентированного простого графа, заданного списком инцидентности СПИСОК (СПИСОК[v] -список вершин, смежных (инцидентных) с вершиной v) легко описать с помощью следующей рекурсивной процедуры:
1 procedure ПОИСК_В_ГЛУБИНУ_В_ГРАФЕ _G(v) {поиск в глубину из вершины v; переменные НОВЫЙ, ЗАПИСЬ - глобальные} 2 beginрассмотретьv; НОВЫЙ[v] := ложь; 3 foruÎЗАПИСЬ[v] do 4 ifНОВЫЙ[u] thenПОИСК_В_ГЛУБИНУ_В_ГРАФЕ _G(u) 5 end{вершина v использована} Поиск в глубину в произвольном, необязательно связном, неориентированном простом графе проводится по следующему алгоритму: Begin 2 forvÎV doНОВЫЙ[v]:=истина; {инициализация} 3 forvÎV do 4 ifНОВЫЙ[v] thenПОИСК_В_ГЛУБИНУ_В_ГРАФЕ _G(v) End Покажем теперь, что этот алгоритм просматривает каждую вершину в точности один раз и его сложность порядка O(n+m). Отметим сначала, что вызов ПОИСК_В_ГЛУБИНУ_В_ГРАФЕ _G(v) влечет за собой просмотр всех вершин связной компоненты графа, содержащей v (если НОВЫЙ[u] = истинадля каждой вершины u этой компоненты). Это непосредственно следует из структуры процедуры ПОИСК_В_ГЛУБИНУ_В_ГРАФЕ _G(v): после посещения вершины (строка 2) следует вызов процедуры для всех ее новых соседей. Отметим также, что каждая вершина графа просматривается не более одного раза, так как просматриваться может только вершина v, для которой
Рис 3. 3. На рис. 3.3. показан граф, вершины которого перенумерованы (номера в скобках) в соответствии с тем порядком, в котором они просматриваются в процессе поиска в глубину (мы отождествляем вершины графа с числами 1, ... , 13 и полагаем, что в списке СПИСОК[v]вершины упорядочены по возрастанию). Алгоритм начинает поиск поочередно от каждой еще не просмотренной вершины, следовательно, просматриваются все вершины графа (необязательно связного). Чтобы оценить сложность алгоритма, отметим сначала, что число шагов в обоих циклах (строки 2 и 3алгоритма) порядка n, не считая шагов, выполнение которых инициировано вызовом процедуры ПОИСК_В_ГЛУБИНУ_В_ГРА ФЕ _G. Эта процедура выполняется не более n раз во втором цикле сразу после посещения каждой вершины для каждого из ее новых соседей, итого суммарно O(n+m) раз. Полное число шагов, выполняемое циклом в строке 3 процедуры ПОИСК_В_ГЛУБИНУ_В_ГРАФЕ _G, для всех вызовов этой процедуры будет порядка m, где m - число ребер. Это дает общую сложность алгоритма O(n+m). Отметим, что алгоритм поиска в глубину в графе легко модифицировать так, чтобы он вычислял связные компоненты графа. В связи с тем, что поиск в глубину играет важную роль в проектировании алгоритмов на графах, представляет интерес нерекурсивная версия процедуры ПОИСК_В_ГЛУБИНУ_В_ГРАФЕ _G. Рекурсия устраняется стандартным способом при помощи стека. Каждая просмотренная вершина помещается в стек и удаляется из стека после ее использования. Метод поиска в глубину очевидным образом переносится на ориентированные графы. Поиск в ширину в графе Теперь рассмотрим несколько иной метод поиска в графе, называемый поиском в ширину. Прежде чем описать его, отметим, что при поиске в глубину чем позднее будет посещена вершина, тем раньше она будет использована - точнее, так будет при допущении, что вторая вершина посещается перед использованием первой. Это прямое следствие того факта, что просмотренные, но еще не использованные вершины накапливаются в стеке. Поиск в ширину основывается, грубо говоря, на замене стека очередью. После такой модификации чем раньше посещается вершина (помещается в очередь), тем раньше она используется (удаляется из очереди). Использование вершины происходит с помощью просмотра всех еще непросмотренных соседей этой вершины. Вся процедура представлена ниже: 1 procedureПОИCК_В_ШИРИНУ_В_ГРАФЕ (v); {поиск в ширину в графе с началом в вершине v; переменные НОВЫЙ, СПИСОК - глобальные} Begin 3ОЧЕРЕДЬ := Æ; ОЧЕРЕДЬ Ü v; НОВЫЙ [v]:= ложь; 4 whileОЧЕРЕДЬ ¹ Æ do 5 beginp Ü ОЧЕРЕДЬ; посетить p; 6 foru Î ЗАПИСЬ [ p] do 7 ifНОВЫЙ [ u] then 8 beginОЧЕРЕДЬ Ü u; НОВЫЙ [ u ]:= ложь End End 11 end{вершина v использована} Способом, аналогичным тому, который был применен для поиска в глубину, можно легко показать, что вызов процедуры ПОИCК_В_ШИРИНУ_ В_ГРАФЕ (v) приводит к посещению всех вершин связной компоненты графа, содержащей вершину v, причем каждая вершина просматривается в точности один раз. Вычислительная сложность алгоритма поиска в ширину также имеет порядок m+n, так как каждая вершина помещается в очередь и удаляется из очереди в точности один раз, а число итераций цикла 6, очевидно, будет иметь порядок числа ребер графа.
На рис. 3.4 представлен граф, вершины которого занумерованы (в скобках) согласно очередности, в которой они посещаются в процессе поиска в ширину. Как и в случае поиска в глубину, процедуру ПОИCК_В_ШИРИНУ_ В_ГРАФЕ (v) можно использовать без всяких модификаций и тогда, когда список инцидентности СПИСОК [ v ], v Î V, определяет некоторый ориентированный граф. Очевидно, что тогда посещаются только те вершины, до которых существует путь от вершины, с которой мы начинаем поиск. Пути и циклы Путем в ориентированном или неориентированном графе G = <V, E>называют последовательность ребер вида <(v1 ,v2), (v2, v3), ...(vn-1,vn)> = S = <E1, ... , En-1 >, где Ei = (vi , vi+1) ÎE, Ei и Ei+1 инцидентны одной вершине. Говорят, что этот путь идет из v1 в vn и имеет длину n - 1.Часто такой путь представляют последовательностью вершин < v1, ... , vn> ,<vi ,vi+1> ÎE , лежащих на нем. В вырожденном случае одна вершина обозначает путь длины 0, идущий из этой вершины в нее же. Путь называется простым, если все ребра и все вершины на нем, кроме быть может первой и последней, различны. Цикл - это простой путь длины не менее 1, который начинается и заканчивается в одной и той же вершине. Заметим, что в неориентированном простом графе длина цикла должна быть не менее 3. Оба вида поиска в графе - в глубину и в ширину - могут быть использованы для нахождения пути между фиксированными вершинами v и u. Достаточно начать поиск в графе с вершины v и вести его до момента посещения вершины u. Преимуществом поиска в глубину является тот факт, что в момент посещения вершины u стек содержит последовательность вершин, определяющих путь из v в u. Это становится очевидным, если отметить, что каждая вершина, помещаемая в стек, является смежной с верхним элементом стека. Однако недостатком поиска в глубину является то, что полученный таким образом путь в общем случае не будет кратчайшим путем из v в u. От этого недостатка свободен метод нахождения пути , основанный на поиске в ширину. Модифицируем процедуру ПОИCК_В_ШИРИНУ_В_ГРА ФЕ, заменяя строки 7-9 на ifНОВЫЙ [ u ] then beginОЧЕРЕДЬ Ü u; НОВЫЙ [ u ]:= ложь ПРЕДЫДУЩИЙ [ u ] :=p End По окончании работы модифицированной таким образом процедуры массив ПРЕДЫДУЩИЙ содержит для каждой просмотренной вершины u вершину ПРЕДЫДУЩИЙ[u], из которой мы попали в u. Отметим, что кратчайший путь из вершины u в вершину v обозначается последовательностью вершин u = u1, u2, ... uk=v, где ui+1= ПРЕДЫДУЩИЙ [ui] для 1 £ i < k и k является первым индексом i для которого ui= v. Действительно, в очереди помещены сначала вершины, находящиеся на расстоянии 0 от v (т.е. сама вершина v), затем поочередно все новые вершины, находящиеся на расстоянии 1 от v, и т.д. Под расстоянием здесь мы понимаем длину кратчайшего пути. Предположим теперь, что мы уже рассмотрели все вершины, находящиеся на расстоянии, не превосходящем r от v, что очередь содержит все вершины, находящиеся на расстоянии r от v, и только эти вершины и что массив ПРЕДЫДУЩИЙ правильно определяет кратчайший путь от каждой, уже просмотренной вершины до вершины v способом, описанным выше. Использовав каждую вершину p, находящуюся в очереди, наша процедура просматривает некоторые новые вершины, и каждая такая новая вершина u находится на расстоянии r + 1 от v, причем, определяя ПРЕДЫДУЩИЙ [u] := p, мы продлеваем кратчайший путь от p до v до кратчайшего пути от u до v. После использования всех вершин из очереди, находящихся на расстоянии r от v, она (очередь), очевидно, содержит множество вершин, находящихся на расстоянии r+1 от v, и легко заметить, что условие индукции выполняется и для расстояния r+1. Связность Пусть граф G - неориентированный. Две вершины a и b называются связанными, если существует путь S с начальной вершиной a и конечной вершиной b, S=< a , a1, ... , an, b >. Если S проходит через какую-нибудь вершину ai более одного раза,то можно, очевидно, удалить его циклический участок и при этом остающиеся ребра будут составлять путь S¢ из a в b. Отсюда следует, что связанные путем вершины связаны и простым путем. Граф называется связным, если любая его пара вершин связана. Для всякого графа существует такое разбиение множества его вершин
на попарно непересекающиеся подмножества вершин Vi, что вершины в каждом Viсвязаны, а вершины из различных Viне связаны. Граф H называется частью графа G, если множество его вершин V(H) содержится во множестве вершин V(G) графа G и все ребра H являются ребрами G. Для любой части H графа G существует единственная дополнительная часть (дополнение) Пусть V¢-подмножество вершин графа G = < V, E >,V¢ÌV. Подграф G(V¢,E¢), определяемый множеством V¢, есть такая часть графа G, множеством вершин которой является V¢, а ребрами - все ребра из G, оба конца которых лежат в V¢:
Тогда в соответствии с разбиением
графа G на непересекающиеся связные подграфы G(Vi). Эти подграфы называются связными компонентами (или компонентами связности) графа G. Теорема 3.2. Если в конечном неориентированном простом графе G ровно две вершины a0 и b0 имеют нечетную локальную степень, то они связаны. Доказательство. По теореме 3.1, каждый конечный граф имеет четное число вершин нечетной степени. Так как это условие выполняется и для той компоненты G, которой принадлежит a0 , то b0 принадлежит той же компоненте связности. ð Теорема 3.3. Если неориентированный простой граф G имеет n вершин и k связных компонент, то максимальное число ребер в G равно
Доказательство. Пусть в графе G связная компонента Gi имеет niвершин. Тогда максимальное число ребер в G равно Из теоремы 3.3 следует для случая k = 2 следующее утверждение. Теорема 3.4. Простой неориентированный граф с n вершинами и с числом ребер, большим, чем
связен. Деревья Связный неориентированный граф называется деревом, если он не имеет циклов. В частности, дерево не имеет петель и кратных ребер. Граф без циклов есть граф, связные компоненты которого являются деревьями; иногда такой граф называется лесом. Любая часть такого графа также будет графом без циклов. Теорема 3.5. В дереве любые две вершины связаны единственным простым путем. Доказательство. Любой путь в графе без циклов является простым. Если бы было два связывающих вершины простых пути, то был бы и цикл в дереве, что невозможно. ð Наглядное представление для произвольного дерева T = <V, E> можно получить при помощи следующей конструкции. Выберем произвольную вершину a0и будем рассматривать ее как корень дерева или вершину нулевого уровня. U0= {a0}. От a0 проведем все ребра к вершинам, находящимся на расстоянии 1 от вершины a0. Вершины, смежные с a0составят множество вершин первого уровня:
От этих вершин первого уровня проведем все ребра к смежным с ними вершинам, находящимся на расстоянии 2 от a0, за исключением ребер, инцидентных вершинам первого уровня. Получим множество вершин второго уровня
Из вершины ai(n) находящейся на расстоянии n от a0, выходит одно ребро к единственной предшествующей вершине
Ни для какой из этих вершин a(n) не может быть ребер, соединяющих ее с вершинами с тем же или меньшим расстоянием, кроме { a(n-1), a(n)}. Таким образом, дерево может быть представлено в следующей форме:
Будем называть вершину a дерева концевой, если r(a) = 1. Будем называть ребро концевым, если хотя бы одна инцидентная ему вершина является концевой. Утверждение 3.6.Любое нетривиальное конечное дерево имеет хотя бы две концевые вершины и хотя бы одно концевое ребро. Доказательство совершенно просто может быть проведено, например, индукцией по числу вершин. Утверждение 3.7. Каждое дерево с n вершинами имеет n-1 ребро. Доказательство. Доказательство легко проводится индукцией по числу вершин. Для n =1 утверждение, очевидно, справедливо. Пусть n>1. Тогда в дереве существует концевая вершина v. Удаляя из дерева v и ребро (u, v), инцидентное v, получим дерево с n-1 вершиной, которое в силу индуктивного предположения имеет n-2 ребра. Следовательно, первоначальное дерево имеет n-2+1=n-1 ребро.ð Обратимся теперь к вопросу о подсчете числа деревьев, которые могут быть построены на заданном множестве вершин. Подчеркнем, что речь идет не о подсчете числа различных попарно неизоморфных деревьев, а именно о числе деревьев, графы которых различны, то есть различаются хотя бы одним ребром (множество вершин фиксировано). Пример. Пусть количество вершин n равно 4. Тогда на этом множестве вершин могут быть построены следующие различные деревья. Первый класс таких деревьев составляют деревья следующего вида:
Концевые вершины для деревьев такого класса могут быть выбраны Второй класс деревьев имеет вид:
Центральная вершина может быть выбрана 4 способами, что дает 4 различных дерева в этом классе. Других деревьев с 4 вершинами, отличных от указанных в первом и втором классах, нет. Таким образом, существует 16 деревьев, имеющих 4 фиксированные вершины. ð Обратимся теперь к общему результату. Теорема 3.8.Число различных деревьев, которые можно построить на заданном множестве V, содержащем n вершин, равно tn= nn-2. Доказательство. Обозначим элементы данного множества V, расположенные в некотором фиксированном порядке, числами V = {1,2, ... ,n} (3.1) Для любого дерева T, определенного на V, введем некоторый символ, характеризующий его однозначно. ВT существуют концевые вершины. Обозначим через b1 первую концевую вершину в последовательности (3.1), а через e1 = {a1, b1} - соответствующее концевое ребро. Удалив из T ребро E1и вершину b1, мы получим новое дерево T1. Для T1найдется первая в списке (3.1) концевая вершина b2 с ребром e2= {a2, b2 }. Эта редукция повторяется до тех пор, пока после удаления ребра en-2= (an-2, bn-2)не останется единственное ребро en-1= (an-1, bn-1), соединяющее две оставшиеся вершины. Тогда список s(T) = [a1, a2, ... , an-2 ] (3.2) однозначно определяются деревом T и двум различным деревьям Tи T¢, очевидно, соответствуют разные символы такого вида. Каждая вершина aiпоявляется в (3.2) r(ai) - 1раз. Для ясности приведем несколько примеров деревьев и соответствующих им последовательностей s(T). Примеры. 1.
2.
3.
Наоборот, каждая последовательность (3.2) определяет дерево T с помощью обратного построения. Если дана последовательность (3.2), то находится первая вершина b в списке (3.1), которая не содержится в (3.2). Это определяет ребро e1 = {a1, b1}.Далее удаляем вершины a1 из последовательности (3.2) и b1из списка (3.1) и продолжаем построение для оставшихся элементов. Получающийся в результате построения граф является деревом, что может быть установлено, например, по индукции. После удаления e1последовательность (3.2) будет содержать n - 3 элемента. Если она соответствует дереву T1, то граф T, получаемый из него добавлением e1, также есть дерево, так как вершина b1не принадлежит T1. B (3.2) каждая вершина может принимать все n возможных значений. Все они соответствуют различным деревьям, откуда и получается формула tn= nn-2. ð Остовное дерево (каркас) Для связного неориентированного графа G = < V, E > без петель каждое дерево < V, T > , содержащее все вершины графа G, где T Í E, будем называть остовным деревом (каркасом) графа G. Напомним, что длина пути есть количество составляющих его ребер. Процедуры поиска в глубину и в ширину можно простым способом использовать для нахождения остовных деревьев. В обоих случаях достижение новой вершины u из вершины v вызывает включение в дерево ребра (v, u). Приведем алгоритм построения остовного дерева методом поиска в глубину. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 E ?” может быть получен за один шаг.
E ?” может быть получен за один шаг.

 Рис. 3. 4.
Рис. 3. 4.

 , состоящее из всех ребер графа G, которые не вошли в H, и инцидентных им вершин. Особенно важным типом частей являются подграфы.
, состоящее из всех ребер графа G, которые не вошли в H, и инцидентных им вершин. Особенно важным типом частей являются подграфы.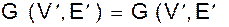 =
=  .
. мы получаем прямое разложение
мы получаем прямое разложение
 .
. . Это число достигается, когда каждый из графов Giполный и имеет niвершин. Допустим, что среди графов Giнайдутся хотя бы два, которые имеют более одной вершины, например n2 ³ n1> 1. Построим вместо G другой граф G¢с тем же числом вершин и компонент, заменяя G1и G2полными графами G1¢и G2¢ соответственно с n1-1 и n2+1 вершинами. Легко видеть, что это увеличит число ребер. Таким образом максимальное число ребер должен иметь граф, состоящий из k -1 изолированных вершин и одного полного графа с
. Это число достигается, когда каждый из графов Giполный и имеет niвершин. Допустим, что среди графов Giнайдутся хотя бы два, которые имеют более одной вершины, например n2 ³ n1> 1. Построим вместо G другой граф G¢с тем же числом вершин и компонент, заменяя G1и G2полными графами G1¢и G2¢ соответственно с n1-1 и n2+1 вершинами. Легко видеть, что это увеличит число ребер. Таким образом максимальное число ребер должен иметь граф, состоящий из k -1 изолированных вершин и одного полного графа с 
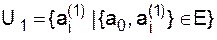 .
. .
. , а также некоторое семейство ребер к вершинам
, а также некоторое семейство ребер к вершинам  , находящимся на расстоянии n +1.
, находящимся на расстоянии n +1. .
.

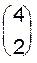 способами, при каждом таком выборе порядок внутренних вершин может быть выбран двумя способами. Получаем 12 различных деревьев, составляющих указанный класс.
способами, при каждом таком выборе порядок внутренних вершин может быть выбран двумя способами. Получаем 12 различных деревьев, составляющих указанный класс.

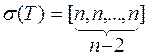



 ð
ð