
|
|
Производная и ее применение1. Найти производные функций
2. Найти производную 2-го порядка от функций: 1) 3. Найти производные от у по х:
4. Найти интервалы монотонности данных функций:
5. Провести полное исследование функций и построить ее график:
6. Найти дифференциалы второго порядка от функций: 1) y= 2) y= 4- x
7. Найти пределы по правилам Лопиталя. 1) 7) 9) Определенный интеграл Вычислить следующие определенные интегралы.
Несобственные интегралы
1. Вычислить несобственный интеграл первого рода
2. Вычислить несобственный интеграл второго рода
Обыкновенные дифференциальные уравнения Дифференциальные уравнения первого порядка С разделяющимися переменными А. Найти общий интеграл уравнения
Б. Найти частный интеграл уравнения 1.
2. Однородные дифференциальные уравнения
А. Найти общий интеграл уравнения 1. 3.
Б. Найти частный интеграл уравнения 1.
3. Линейные дифференциальные уравнения
А. Найти общее решение уравнения 1. 3.
Б. Найти частное решение уравнения 1. 3. Линии второго порядка 1. Составить уравнение окружности с центром в точке (1;2) и проходящей через точку (-3;-4). 2. Составить уравнение окружности, зная, что она проходит через точки А(0;1), B(-2;0), C(2;0). 3. Найти уравнение окружности, касающейся осей координат, если центр лежит в точке с координатами (a;-а). 4. Дан эллипс 2х2 + 3у2 = 18, найти его полуоси, фокусы, эксцентриситет, уравнение директрис. 5. Составить уравнение линии, сумма расстояний точек которой до точек А(2;4) и В (-4;4) равно 8. 6. Составить уравнение параболы, вершина которой находится в начале координат, зная, что парабола расположена симметрично относительно оси Оx и проходит через точку А(3;6). 7. Составить уравнение параболы, вершина которой находится в начале координат, зная, что парабола расположена в правой полуплоскости симметрично относительно оси Оx и ее параметр р=5. 8. Составить уравнение параболы, вершина которой находится в начале координат, зная, что парабола расположена в верхней полуплоскости симметрично оси Оy и ее параметр р=2. 9. Составить уравнение геометрического места точек, одинаково удаленных от точки F(0;1) и от прямой у=3. 10. Найти координаты вершины параболы, заданной уравнением х = 2у2 + 4у-5. Написать уравнение оси симметрии параболы.
Вопросы к зачету 1. Понятие множества. 2. Операции над множествами. 3. Свойства числовых множеств и последовательностей. 4. Точечные множества в N-мерном пространстве. 5. Евклидово пространство. 6. Понятие окрестности точки. 7. Функциональная зависимость. 8. Графики и свойства основных элементарных функций. 9. Предел числовой последовательности. 10. Предел функции. 11. Основные теоремы о пределах. 12. Первый и второй замечательные пределы. 13. Раскрытие неопределенностей, правило Лопиталя. 14. Непрерывность функции в точке и на интервале. 15. Свойства непрерывных функций. 16. Точки разрыва первого и второго рода. 17. Нахождение асимптот функции. 18. Производная и дифференциал. 19. Основные теоремы о дифференцируемых функциях. 20. Выпуклость функции. 21. Производная сложной функции. 22. Функции нескольких переменных и их непрерывность. 23. Производные функции нескольких переменных. 24. Дифференциалы функции нескольких переменных. 25. Классические методы оптимизации функций одной и двух переменных. 26. Поиск экстремума функции одной переменной. 27. Поиск экстремума функции двух переменных. 28. Неопределенный интеграл, основные теоремы. 29. Определенный интеграл, основные теоремы. 30. Несобственные интегралы. 31. Интегрирование подстановкой. 32. Интегрирование по частям. 33. Интегрирование рациональных функций. 34. Функции спроса и предложения. 35. Функция полезности. 36. Кривые безразличия.
Вопросы к экзамену 1. Графики и свойства основных элементарных функций. 2. Предел функции. 3. Основные теоремы о пределах. 4. Непрерывность функции в точке и на интервале. 5. Производная и дифференциал. 6. Основные теоремы о дифференцируемых функциях. 7. Функции нескольких переменных и их непрерывность. 8. Производные функции нескольких переменных. 9. Дифференциалы функции нескольких переменных. 10. Поиск экстремума функции одной переменной. 11. Поиск экстремума функции двух переменных. 12. Неопределенный интеграл, основные теоремы. 13. Определенный интеграл, основные теоремы. 14. Интегрирование подстановкой. 15. Интегрирование по частям. 16. Интегрирование рациональных функций. 17. Системы линейных уравнений. 18. Определители, свойства. 19. Матрицы, классификация. 20. Операции над матрицами. 21. Прямая линия на плоскости. 22. Эллипс. 23. Гипербола. 24. Парабола. 25. Прямая и плоскость в пространстве. 26. N-мерное линейное векторное пространство. 27. Системы векторов, операции над ними. 28. Ранг матрицы. 29. Линейные операторы и матрицы. 30. Собственные векторы линейных операторов. 31. Решение системы линейных уравнений с помощью определителей. 32. Решение системы линейных уравнений в матричной форме. 33. Решение системы линейных уравнений методом Гаусса. 34. Задачи линейного программирования. 35. Теория двойственности. 36. Графическое решение задачи линейного программирования. 37. Симплексный метод. 38. Транспортная задача. 39. Решение транспортной задачи методом потенциалов. 40. Дискретное программирование. 41. Нелинейное программирование. 42. Динамическое программирование.
Литература 1. Бермант А.Р., Араманович И.Г. Краткий курс математического анализа. 1973. 2. Блох Э.Л, Лошинский Л.И., Турин В.Я. Основы линейной алгебры и некоторые ее приложения. 1971. 3. Воеводин В.В. Линейная алгебра. 1974. 4. Высшая математика для экономистов./ Под ред. Кремера Н.Ш. 2002. 5. Гельфанд И.М. Лекции по линейной алгебре. 1971. 6. Глухов В.В., Медников М.Д., Коробко С.Б. Математические методы и модели для менеджмента. 2000. 7. Глухов В.В., Медников М.Д., Коробко С.Б. Экономико-математические методы и модели в менеджменте. 2000. 8. Данко П.Е., Попов А.Г., Кожевникова Т.Н. Высшая математика в упражнениях и задачах. Ч.1. 1986. 9. Карасев А.И. Курс высшей математики для экономических вузов. Ч. 1, 2. 1982. 10. Кирилов А.Л. Математика для управленцев. 2000. 11. Клетеник Д.Б.. Сборник задач по аналитической геометрии. 1975 (и последующие издания). 12. Минорский В.П. Сборник задач по высшей математике. 1964 (и последующие издания). 13. Проскуряков И.В. Сборник задач по линейной алгебре. 2000. 14. Таха Х. Введение в исследование операций. 1985. 15. Тугуз Ю.Р. Математика. 2003. 16. Щипачев В.С. Курс высшей математики. 2005.
Учебное издание

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|











 ; 2)
; 2)  ; 3)
; 3) 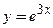 ; 4)
; 4)  .
.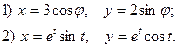

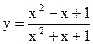






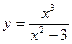
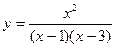








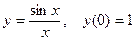
 ;
; .
. ; 2)
; 2)  ; 3).
; 3). 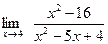 ; 4)
; 4)  5)
5)  ; 6).
; 6).  ;
; ; 8)
; 8)  ;
; n>0 ; 10)
n>0 ; 10)  ; 11).
; 11). 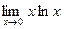 .
.

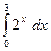

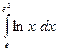


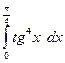




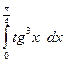
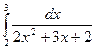


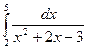
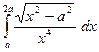









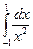
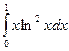





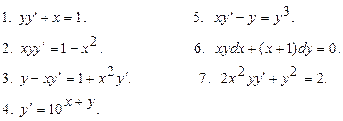
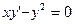 .
.
 .
.
 .
.
 .
.
 .
.
 . 2.
. 2.  .
. 2.
2.  .
. .
. . 2.
. 2.  .
. . 2.
. 2.  .
. . 4.
. 4. 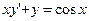 .
.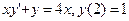 . 2.
. 2.  .
. . 4.
. 4.  .
.