
|
|
Полярная система координат
Полярная система координат — система координат, ставящая в соответствие каждой точке на плоскости пару чисел (ρ,φ). Основными понятиями этой системы являются точка отсчёта O (полюс) и луч Ox, начинающийся в этой точке (полярная ось). Координата ρ определяет расстояние от точки до полюса, координата φ — угол между полярной осью и отрезком, соединяющим полюс и рассматриваемую точку. Координата φ берётся со знаком «+», если угол от оси до отрезка вычисляется против часовой стрелки, и со знаком «-» в противоположном случае. Любая точка в этой системе имеет бесконечное число координат вида (ρ,φ+2πn), которым соответствует одна и та же точка при любых натуральных n. Для полюса ρ = 0, а угол φ произвольный. Иногда допускаются отрицательные значения ρ, в этом случае координаты (ρ,φ) и ( - ρ,φ + π) определяют одну и ту же точку плоскости. Примеры использования. Уравнение прямой на расстоянии D от полюса: ρ = D / cos(φ + α). Уравнение окружности с центром в полюсе и радиуса R: ρ = R. Уравнение окружности, проходящей через полюс, и радиуса R: Уравнение эллипса с фокусом в полюсе: Формулы перехода. От полярной системы координат к декартовой:
От декартовой системы координат к полярной:
Скалярное произведение двух векторов Определение скалярного произведения (СП) Определение.СП двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение будем обозначать символом По определению:
Можно сформулировать другое определение СП двух векторов, эквивалентное определению. Из теоремы имеем:
(проекция вектора Отсюда получаем Определение:
(2)
Геометрические свойства СП Теорема.Необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения. Доказательство.1). Необходимость. Пусть векторы 2). Достаточность. Пусть Если же векторы Замечание. Углом между двумя векторами считаем тот, который не превосходит p. (0 £ j £p) Из формулы (1) следует Теорема. Два ненулевых вектора Алгебраические свойства СП 1. 2. 3. 4.
Свойство 1 следует из формулы (1). Второе свойство получается из определения (формула 2) скалярного произведения:
Свойство 3 получаем из свойств линейности проекции вектора на ось
Четвертое свойство вытекает из формулы (1):
Выражение скалярного произведения (СП) Теорема.Если два вектора
то СП этих векторов равно сумме попарных произведений их соответствующих координат:
Доказательство.По определению 1 также
Используя алгебраические свойства СП, имеем
Следствие 1.Необходимым и достаточным условием ортогональности векторов
Следствие 2.Угол j между векторами
Векторное произведение двух векторов Правые и левые тройки векторов и системы координат Определение.Три вектора называются упорядоченной тройкой (или просто тройкой), если указано, какой из них является первым, какой- вторым и какой- третьим. Т.е. запись Определение.Тройка некомпланарных векторов
Правая тройка Левая тройка Определение.Аффинная или декартова система координат называется правой (левой), если три базисных вектора образуют правую (левую) тройку. В дальнейшем будем рассматривать только правые системы координат. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

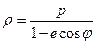 .
.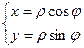
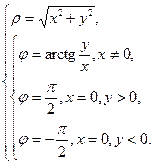
 , угол между векторами - j.
, угол между векторами - j. (1)
(1)
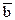 на ось вектора
на ось вектора  ).
). или
или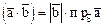
 ортогональны, j- угол между ними. Тогда cosj=0 и, в силу формулы (1) ,
ортогональны, j- угол между ними. Тогда cosj=0 и, в силу формулы (1) ,  .
. . Докажем, что векторы
. Докажем, что векторы  является нулевым, то он ортогонален любому вектору.
является нулевым, то он ортогонален любому вектору. , поэтому из равенства
, поэтому из равенства  вытекает, что cosj=0, т.е. векторы ортогональны, ч.т.д.
вытекает, что cosj=0, т.е. векторы ортогональны, ч.т.д.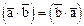
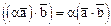
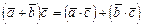
 , если
, если  , если
, если  .
. и формулы (2) :
и формулы (2) :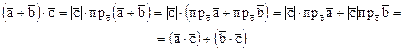
 .
.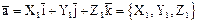 ,
,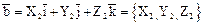 ,
, .
.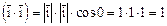 ,
, .
. , также
, также .
.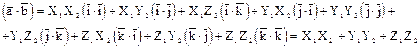
 и
и  является равенство
является равенство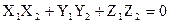 .
. .
. означает, что первым элементом является вектор
означает, что первым элементом является вектор  .
.
