
|
|
Некоторые дополнительные предложения и примеры1) В аналитической геометрии часто требуется составить уравнение прямой, зная две ее точки. Решим эту задачу в общем виде, считая данными две произвольные точки: М1(x1;y1; z1) и М2(x2;y2; z2). Для решения задачи достаточно заметить, что в качестве направляющего вектора рассматриваемой прямой можно взять вектор
Это и есть искомые (канонические) уравнения прямой, проходящей через две данные точки: М1(x1;y1; z1) и М2(x2;y2; z2). 2) Решим также в общем виде задачу: составить уравнение плоскости, проходящей через три различные точки: М1(x1;y1; z1); М2(x2;y2; z2); М3(x3;y3; z3). Обозначим через x, y, z координаты произвольной точки М пространства и рассмотрим три вектора:
Точка М лежит на плоскости М1М2М3 в том и только в том случае, когда векторы В нашем случае имеем:
Это и есть искомое уравнение плоскости, проходящей через точки М1, М2, М3, так как ему удовлетворяют координаты x, y, z точки М в том и только в том случае, когда она лежит в этой плоскости. 3) Угол между двумя прямыми. Углом между двумя прямыми в пространстве называют любой из углов, образованных двумя прямыми, проведенными из одной точки параллельно данным прямым. Если прямые параллельны, то угол между ними считается равным нулю или p. Пусть даны уравнения двух прямых:
Обозначим угол между прямыми через a, а угол между их направляющими векторами
Так как a=j или a=p - j, то cosa=±cosj. Следовательно,
или в координатной форме:
Формулы (2) и (3) являются формулами для определения угла между двумя прямыми в пространстве. 4) Условия параллельности и перпендикулярности двух прямых в пространстве. Для того, чтобы две прямые были параллельны, необходимо и достаточно, чтобы их направляющие векторы
Условие (4) является условием параллельности двух прямых в пространстве. Для того, чтобы прямые были перпендикулярны между собой, необходимо и достаточно, чтобы направляющие их векторы Условие ортогональности двух векторов m1m2+n1n2+p1p2=0 (5) является условием перпендикулярности двух прямых в пространстве. Пример. Найти уравнение прямой, проходящей через точку М(3; 2; -1) перпендикулярно двум прямым:
Составим уравнение любой прямой, проходящей через точку М:
Используя условие перпендикулярности искомой прямой к прямой а1, а затем к прямой а2, получим
4m+n-2p=0. Из этой однородной структуры линейных уравнений с неизвестными m, n, p найдем отношения неизвестных:
Подставляя в уравнения прямой (6) вместо m, n, p пропорциональные им величины, получим искомые уравнения:
5) Углом между прямой и плоскостью называют любой из двух смежных углов, образованных прямой и ее проекцией на плоскость. Пусть дано уравнение плоскости П: Ax+By+Cz+D=0 и уравнение прямой
Обозначим угол между векторами
При этом sina=±cosj. Следовательно,
или, в координатной форме,
Для того, чтобы плоскость П была параллельна прямой , необходимо и достаточно, чтобы векторы Условие ортогональности двух векторов ( или в координатной форме: Am+Bn+Cp=0. Для того, чтобы прямая Условие коллинеарности двух векторов ( или
Пример. Составить уравнение плоскости П, проходящей через точку М(-1; 2; -3) параллельно двум прямым:
Напишем уравнение связки плоскостей с центром в точке М: A(x+1)+B(y-2)+C(z+3)=0. Используем условие параллельности плоскости П и прямой
2А-3В+С=0 Из этой системы однородных уравнений определим отношения коэффициентов А, В, С и затем в уравнение (4) вместо коэффициентов А, В, С подставим пропорциональные им величины:
11(x+1)+13(y-2)+17(z+3)=0; 11x+13y+17z+36=0. 6) Пучок плоскостей. Через всякую прямую в пространстве можно провести бесчисленное множество плоскостей. Совокупность всех плоскостей, проходящих через одну и ту же прямую, называется пучком плоскостей. Пусть дано уравнение прямой как линии пересечения двух плоскостей:
Составим уравнение: A1x+B1y+C1z+D1+l(A2x+B2y+C2z+D2)=0, (8) где l – произвольное число. При любом l это уравнение первой степени, кроме того, при любом l это уравнение определяет плоскость, проходящую через прямую (7). Действительно, если точка М0 принадлежит прямой (7), то:
и, следовательно A1x0+B1y0+C1z0+D1+l(A2x0+B2y0+C2z0+D2)=0. Уравнение (8) называется уравнением пучка плоскостей, проходящих через прямую (7). Уравнение (8) дает любую плоскость пучка, за исключением плоскости A2x+B2y+C2z+D2=0. Пример. Найти проекцию прямой
На плоскость 3x-4y+z-8=0 (П). Составим уравнение пучка плоскостей, проходящих через прямую (9): 2x-3y+4z-1+l(x+5y-2z+3)=0 (10) или (2+l)x+(5l-3)y+(4-2l)z+(3l-1)=0. Определим l, используя условие перпендикулярности плоскостей: 3(2+l)-4(5l-3)+(4-2l)=0. Откуда , Уравнения искомой проекции можно записать как уравнения линии пересечения плоскостей:
Пример. Составить уравнение плоскости, проходящей через прямую Решение. Составим уравнение пучка плоскостей, проходящих через первую из данных прямых: 3x+2y+5z+6+l(x+4y+3z+4)=0 (*) Преобразуем это уравнение: (3+l)x+(2+4l)y+(5+3l)z+(6+4l)=0. Используя условие параллельности прямой и плоскости получим: 3(3+l)+2(2+4l)-3(5+3l)=0. Отсюда l=1. Подставляя найденное значение l в уравнение (*), найдем: 4x+6y+8z+10=0 или 2x+3y+4z+5=0. Пример. Найти расстояние от точки М(1; 2; 3) до прямой
Решение. Проведем через М плоскость П, перпендикулярную к данной прямой и найдем точку Р, где эта плоскость пересекает данную прямую. Искомое расстояние от точки М до данной прямой будет равно расстоянию от точки М до точки Р. Искомое уравнение плоскости П можно записать в виде: A(x-1)+B(y-1)+C(z-1)=0; эта плоскость должна быть перпендикулярна к данной прямой. По условию перпендикулярности прямой к плоскости имеем:
Выбирая здесь множитель пропорциональности для простоты равным единице, находим А=2, В=5, С=-2. Итак, плоскость имеет уравнение 2(x-1)+5(y-1)-2(z-1)=0 или 2x+5y-2z=0. Теперь мы должны найти точку Р, в которой эта плоскость пересекается с данной прямой. Для этого нужно уравнение данной прямой решить совместно с найденным уравнением плоскости П:
Отсюда x=2t+11, y=5t+18, z=4-2t. Подставляя эти уравнения в уравнение найденной плоскости 2x+5y-2z-5=0, получим: 4t+22+25t+90+4t-8-5=0; 33t=-99; t=-3. Координаты точки Р будут равны x=5, y=3, z=10. Искомое расстояние d от точки М до данной прямой, равное расстоянию между точками М и Р, найдется по формуле нахождения расстояния между двумя точками:
Пример. Определить условие, при котором две прямые
лежат на одной плоскости. Решение. Пусть
Линейная алгебра

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ; отсюда m=x2 - x1; n=y2 - y1; p=z2 - z1, окончательно получим
; отсюда m=x2 - x1; n=y2 - y1; p=z2 - z1, окончательно получим .
. ,
, ,
,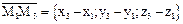 .
. ,
,  и
и 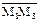 компланарны; условием компланарности этих трех векторов является равенство нулю их смешанного произведения или равенство нулю определителя третьего порядка, составленного из их координат.
компланарны; условием компланарности этих трех векторов является равенство нулю их смешанного произведения или равенство нулю определителя третьего порядка, составленного из их координат. .
.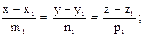
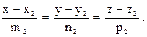
 и
и  - через j. При этом
- через j. При этом (1)
(1) (2)
(2) (3)
(3) (4)
(4) ;
;  .
. (6)
(6) 2m-3n+5p=0,
2m-3n+5p=0,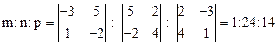 .
. .
. :
: .
. ={А; В; С} – нормальный вектор плоскости;
={А; В; С} – нормальный вектор плоскости; ={m; n; p} – направляющий вектор прямой.
={m; n; p} – направляющий вектор прямой. .
.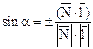
 .
. .
.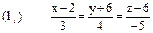 ,
, .
. , а затем и прямой
, а затем и прямой  :
: 3А+4В+5С=0
3А+4В+5С=0 ;
; (7)
(7)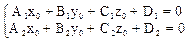
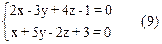
 . Подставив значение в уравнение (10), найдем уравнение проектирующей плоскости:
. Подставив значение в уравнение (10), найдем уравнение проектирующей плоскости: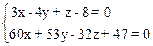
 параллельно прямой
параллельно прямой  .
. .
.
 .
. .
.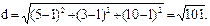
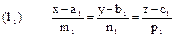 ,
,
 ={a2-a1; b2-b1; c2-c1} и направляющие векторы прямых
={a2-a1; b2-b1; c2-c1} и направляющие векторы прямых  .
.