
|
|
Задачи линейного программирования
Типичной задачей линейного программирования является следующая: найти максимум линейной функции
где cj,aij и bi – заданные числа. Задачи линейного программирования являются математическими моделями многочисленных задач технико-экономического содержания. Рассмотрим несколько типичных задач. Задача о рационе. По заданному ассортименту продуктов, при известном содержании в каждом из них питательных веществ и известной стоимости продуктов, составить рацион, удовлетворяющий необходимым потребностям, с минимальными денежными затратами. Пусть имеются n различных продуктов и m питательных веществ (например, жиров, белков, углеводов, витаминов и др.). Обозначим через aij содержание (в единицах массы) j-го питательного вещества в единице массы i-го продукта; через bj обозначим минимальную (в единицах массы) суточную потребность в j-м питательном веществе. Наконец, через xi обозначим искомое суточное потребление i-го продукта. Очевидно, что xi≥0. Величина
Если ci –стоимость единицы массы i-го продукта, то стоимость всего рациона определяет линейная форма Итак, математическая формулировка задачи выбора рациона состоит в следующем: Найти
при условиях
Эта задача является одной из типичных задач линейного программирования. В постановке задачи вовсе не обязательно было указывать, что это задача о рационе. Достаточно ясно, что таким же образом могут быть сформулированы многочисленные задачи об оптимальных смесях (слово «смесь» здесь следует понимать в обобщенном смысле: это и собственно смесь, и сплав, и рацион, и т.д.). Транспортная задача. Требуется составить план перевозок груза таким образом, чтобы общая стоимость перевозок была минимальной. Исходная информация: аi – количество единиц груза в i-м пункте отправления (i=1,…,m); bj – потребность в j-м пункте назначения (j=1,…,n) в единицах груза; cij-стоимость перевозки единицы груза из i-го пункта в j-й. Обозначим через xij планируемое количество единиц груза для перевозки из i-го пункта в j-й. В принятых обозначениях:
В простейшем случае должны выполняться следующие очевидные условия:
Таким образом, математической формулировкой транспортной задачи будет:
при условиях
Эта задача носит название замкнутой транспортной модели. Заметим, что условие
служит естественным условием разрешимости замкнутой транспортной задачи. Более общей транспортной задачей является так называемая открытая транспортная модель: найти
при условиях
Ясно, что в этой задаче не предполагается, что весь груз, накопленный в i-м пункте, должен быть вывезен. В схему транспортной задачи укладываются и некоторые другие задачи технико-экономического содержания, например, так называемая «задача о выборе»: задача о наиболее экономном (в смысле суммарных затрат времени) распределении n работ между n исполнителями при известном времени, затрачиваемом каждым исполнителем на каждой работе. Данная задача является частной моделью замкнутой транспортной задачи при m=n и всех ai=bi=1. Заметим, что решения транспортных задач обладают свойствами целочисленности, и поэтому эти задачи относят к задачам линейного программирования, в которых целочисленность выступает как необходимое дополнительное условие. Решение основной задачи линейного программирования геометрическим методом является наглядным в случае двух и даже трех переменных. Для случая большего числа переменных геометрический метод становится невозможным. Одним из основных аналитических методов решения задач линейного программирования является симплекс-метод. Система ограничений в вычислительных методах обычно задается системой линейных уравнений: a11x1+a12x2+…+a1nxn=b1, a21x1+a22x2+…+a2nxn=b2, … am1x1+am2x2+…amnxn=bm, и среди неотрицательных решений надо найти такие, которые максимизировали бы линейную функцию L=c1x1+c2x2+…+cnxn+c0. Выразим x1, x2,…,xr (rm) через остальные переменные: x1=a’1,r+1xr+1+…+a’1nxn+b’1, x2=a’2,r+1xr+1+…+a’2nxn+b’2, … xr=a’r,r+1xr+1…+a’rnxn+b’r, где b’1³0, b’2³0,…,b’r³0. Если ограничительные условия заданы неравенствами, то их можно преобразовать в равенства путем введения новых неотрицательных переменных, так называемых балансовых (выравнивающих). Например, в неравенстве a1x1+a2x2+…+anxn£b достаточно добавить к левой части некоторую величину xn+1³0 и получится равенство a1x1+a2x2+…+anxn+xn+1=b. Ограничительные условия могут задаваться и смешанным образом, т.е. неравенствами и уравнениями, тогда указанным путем их можно свести только к уравнениям. Переменные (неизвестные) x1, x2,…,xr называются базисными, а весь набор {x1, x2, …, xr} – базисом, остальные переменные называются свободными, система ограничений называется системой, приведенной к единичному базису. Подставляя в линейную систему формы L вместо базисных переменных их выражения через свободные из системы, получим L=g0+gr+1xr+1+…+gnxn. Теперь, полагая все свободные переменные равными нулю, найдем значения базисных переменных: x1=b’1, x2=b’2,…,xr=b’r. Таким образом, решение (b’1,…,b’r,0,…,0) системы является допустимым – оно называется базисным. Для получения базисного решения значения линейной формы полагаем LБ=g0. Решение задачи с помощью симплекс-метода распадается на ряд шагов, заключающихся в том, что от данного базиса Б мы переходим к другому базису Б’ с таким расчетом, чтобы значение LБ уменьшалось или, по крайней мере, не увеличивалось, т.е. LБ’£LБ. Если система ограничений сведена к единому базису:
xi+….+ai,r+1xr+1+…+ainxn=bi, … xr+…+ar,r+1xr+1…+arnxn=br, а линейная форма L – к виду L+gr+1xr+1+…+gjxj+…+gnxn=g0, то эти данные можно представить в виде таблицы
Равенство L+gr+1xr+1+…+gjxj+…+gnxn=g0 будем называть приведенным (к свободным переменным) выражением для функции L, а коэффициенты gj -оценками (индексами) соответствующих свободных переменных xj. Алгоритм метода будет выглядеть следующим образом: Выбирают разрешающий столбец ap из условия: оценка gp<0 и хотя бы один элемент aip>0. Выбирают q–ю разрешающую строку из условия bq/aqp=min{bi/aip} для aij>0. Производят пересчет элементов разрешающей q-й строки по формуле a’qk=aqk/aqp (k=-,1,…,n). Вычисляют элементы всех остальных строк (при k¹p) по формуле a’ik=aik-a’qkaip (i=0,1,…,q-1,q+1,…,r). 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 при условиях
при условиях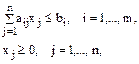
 есть общее содержание j-го питательного вещества в рационе, которое не должно быть меньше минимальной потребности bi:
есть общее содержание j-го питательного вещества в рационе, которое не должно быть меньше минимальной потребности bi: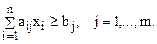
 .
.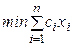
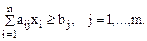
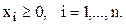
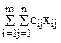 – общая (суммарная) стоимость перевозок;
– общая (суммарная) стоимость перевозок; – количество груза, вывозимого из i-го пункта;
– количество груза, вывозимого из i-го пункта; – количество груза, доставляемого в j-й пункт.
– количество груза, доставляемого в j-й пункт.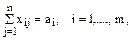
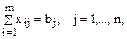
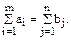
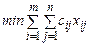

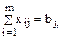
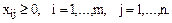
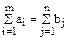
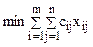
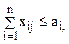
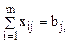
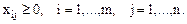
 x1+…+a1,r+1xr+1+…+a1nxn=b1,
x1+…+a1,r+1xr+1+…+a1nxn=b1,