
|
|
Уравнение плоскости в отрезкахПусть в уравнении плоскости Аx+Вy+Сz+D=0 ни один из коэффициентов A, B, C, D не равен нулю. Сделав следующие преобразования: Аx+Вy+Сz=-D;
и вводя обозначения
Это специальный вид уравнения плоскости, называемый уравнением плоскости "в отрезках". Здесь числа a, b, c имеют простой геометрический смысл, а именно a, b, c - это величины отрезков, которые плоскость отсекает на координатных осях. Чтобы убедиться в этом, достаточно найти точки пересечения плоскости с координатными осями. Точка пересечения плоскости с осью Ox определяется из уравнения этой плоскости Пример. Составить уравнение плоскости, зная, что она отсекает на координатных осях отрезки a=3; b=-4; c=2. Решение. На основании предыдущего получаем искомое уравнение сразу:
Нормальное уравнение плоскости. Возьмем в пространстве XYZ некоторую плоскость П. Проведем через начало координат прямую n, перпендикулярную плоскости П. Назовем эту прямую нормалью, - и отметим буквой Р точку пересечения нормали с плоскостью П. На нормали введем положительное направление от начала координат О к точке Р. Если точка Р совпадает с О, т.е. данная плоскость проходит через начало координат, то положительное направление нормали выберем произвольно. Обозначим через a, b, g углы, которые составляет направленная нормаль с осями координат, через р - длину отрезка ОР.
Мы выведем уравнение данной плоскости П, считая известными числа cos a, cos b, cos g и р. С этой целью возьмем на плоскости П произвольную точку М и обозначим через x, y, z ее координаты. Очевидно, проекция вектора прn Заметим, что Из равенств (4) и (5) следует, что x cosa + ycosb + zcosg = р или x cosa + ycosb + zcosg - р=0. (6) Это уравнение плоскости, оно носит специальное название: нормальное уравнение плоскости; в этом уравнении cosa, cosb, cosg суть направляющие косинусы нормали, р - расстояние плоскости от начала координат. Пусть, как и ранее. n нормаль к произвольной плоскости П, М*- произвольная точка пространства, d- ее расстояние от данной плоскости (см. рис. 1). Условимся называть отклонением точки М* от данной плоскости число +d, если М* лежит по ту сторону от плоскости, куда идет положительное направление нормали, -d, если М* лежит с другой стороны от данной плоскости. Отклонение точки от плоскости обозначим буквой d; таким образом, d=± d, причем полезно заметить, что d=+d, когда точка М* и начало координат лежат по разные стороны от плоскости, и d=-d, когда точка М* и начало координат лежат по одну сторону от плоскости (для точек, лежащих на плоскости, d=0). Теорема. Если точка М* имеет координаты (x*; y*; z*), а плоскость задана нормальным уравнением x cosa + ycosb + zcosg - р=0, то отклонение точки М* от этой плоскости задается формулой d= x* cosa + y*cosb + z*cosg - р. (7) Доказательство. Спроектируем точку М* на нормаль; пусть Q - ее проекция (рис. 14); тогда d=PQ=OQ - OP, где PQ, OQ, OP - это величины направленных отрезков нормали: d= Из ранее доказанного Из равенств (8) и (9) получаем: d=x* cosa + y*cosb + z*cosg - р. Теорема доказана. Покажем, как привести общее уравнение плоскости к нормальному виду. Пусть Аx+Вy+Сz+D=0 (10) - общее уравнение некоторой плоскости, а x cosa + ycosb + zcosg - р=0 - ее нормальное уравнение. Так как уравнения (10) и (6) определяют одну и ту же плоскость, то коэффициенты этих уравнений пропорциональны, т.е. mА=cosa, mВ=cosb, mС=cosg, mD= -р. (11) Чтобы найти множитель m, возведем первые три из этих равенств в квадрат и сложим. Получим: m2(А2+В2+С2)= cos2a + cos2b + cos2g. Так как cos2a + cos2b + cos2g=1, то Число m называется нормирующим множителем. Для определения знака нормирующего множителя используем последнее из равенств (11): mD= -р. Следовательно, знак нормирующего множителя противоположен знаку свободного члена нормируемого уравнения. Если D=0, то знак нормирующего множителя можно выбирать по желанию. Пример. Даны плоскость 12х-4y+3z+14=0 и точка М(1; 3; 4). Найти отклонение точки М от данной плоскости. Решение. Приведем данное уравнение к нормальному виду. Найдем нормирующий множитель: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
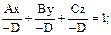
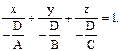
 ;
;  ;
;  , получим
, получим 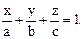
 при условии y=z=0. Отсюда х=а. Таким образом, величина отрезка, отсекаемого плоскостью на оси Ox, действительно равна а. Аналогично, отрезки, отсекаемые плоскостью на осях Oy и Oz, имеют величины, равные соответственно b и c.
при условии y=z=0. Отсюда х=а. Таким образом, величина отрезка, отсекаемого плоскостью на оси Ox, действительно равна а. Аналогично, отрезки, отсекаемые плоскостью на осях Oy и Oz, имеют величины, равные соответственно b и c. или 4x-3y+6z-12=0.
или 4x-3y+6z-12=0.
 на нормаль равна ОР, а так как направление отрезка
на нормаль равна ОР, а так как направление отрезка  положительное, то величина этого отрезка выражается положительным числом р:
положительное, то величина этого отрезка выражается положительным числом р: ,
,  и
и  . Но OQ=
. Но OQ= 
 , ОР=р; следовательно
, ОР=р; следовательно .
. . Умножая данное уравнение на m, получим исходное нормальное уравнение плоскости:
. Умножая данное уравнение на m, получим исходное нормальное уравнение плоскости: 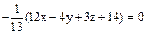 . Подставляя в левую часть этого уравнения координаты точки М, имеем:
. Подставляя в левую часть этого уравнения координаты точки М, имеем:  . Итак, точка М имеет отрицательное отклонение от данной плоскости и удалена от нее на расстояние d=2.
. Итак, точка М имеет отрицательное отклонение от данной плоскости и удалена от нее на расстояние d=2.