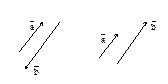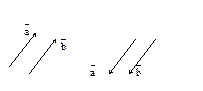|
|
Линейное уравнение первого порядка
Линейным уравнением первого порядка, разрешенным относительно производной, называется уравнение вида y' + p(x)y = f(x), (1) которое при f(x)=0 называется однородным, а при f(x) ≠0 – неоднородным. Для однородного линейного уравнения y′+ р(х)у=0 переменные разделяются, и, поделив это уравнение на у, мы можем при у≠0 переписать его в виде
Интегрирование уравнения (2) приводит к равенству
в котором С1 обозначает произвольную положительную постоянную. Равенство (3) в свою очередь можно переписать в виде двух равенств
Из этих двух равенств вытекает, что
где С1, как и выше, принимает любые положительные значения. Равенства (4) и (5) можно объединить и записать в виде одного равенства
в котором постоянная С≠ 0 принимает любые строго положительные и любые строго отрицательные значения. Функция (6) Остается заметить, что при получении уравнения (2) из указанного однородного линейного уравнения мы производили деление на у и вследствие этого потеряли решение у=0. Учитывая, что потерянное решение у = 0 может быть включено в найденное нами семейство решений (6), если допустить, что постоянная С может быть равна нулю, мы окончательно получим, что общее решение однородного линейного уравнения Для отыскания решения неоднородного линейного уравнения (1) применим так называемый метод вариации постоянной, заключающийся в том, что решение неоднородного уравнения (1) ищется в том же виде (6), что и решение однородного уравнения, но при условии, что С является не постоянной величиной, а искомой функцией С(х). Фактически мы переходим в неоднородном уравнении (1) от искомой функции у(х) к новой искомой функции С(х) с помощью равенства
Дифференцируя равенство (7), получим, что
Подставляя у и у', определяемые равенствами (7) и (8), в уравнение (1), мы получим следующее уравнение:
для определения искомой функции С(х). Из этого уравнения заключаем, что
где С — произвольная постоянная. Подставляя найденное значение (9) функции С(х) в равенство (7), мы получим, что общее решение неоднородного уравнения (1) определяется равенством
в котором С обозначает произвольную постоянную. Таким образом, общее решение неоднородного уравнения (1) равно сумме общего решения (6) соответствующего однородного уравнения и частного решения неоднородного уравнения
получающегося из (10) при С = 0. В качестве примера проинтегрируем неоднородное линейное уравнение
Векторная алгебра
4.1. Понятие вектора и линейные операции Понятие вектора Вектором будем называть направленный отрезок. Обозначать вектор будем либо как направленный отрезок символом
Начало вектора называют точкой его приложения. Длину вектора будем обозначать символом модуля: Вектор называется нулевым,если совпадают его начало и конец. Нулевой вектор имеет длину равную нулю. Векторы называются коллинеарными, если они лежат на параллельных прямых.
Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление. Все нулевые векторы считаются равными.
Точка приложения вектора может быть выбрана производно, поэтому изучаемые векторы называют свободными. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . (2)
. (2)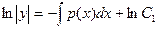 , (3)
, (3)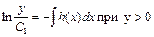 ,
,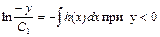 .
.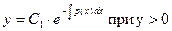 , (4)
, (4)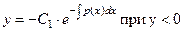 , (5)
, (5)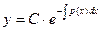 , (6)
, (6) . (7)
. (7)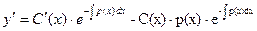 , (8)
, (8)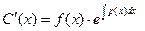
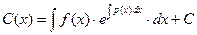 , (9)
, (9) , (10)
, (10)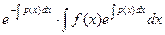 ,
, .Сначала находим общее решение соответствующего однородного уравнения
.Сначала находим общее решение соответствующего однородного уравнения  , являющегося однородным линейным уравнением у'+р(х)у=0 с функцией
, являющегося однородным линейным уравнением у'+р(х)у=0 с функцией 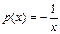 . Общее решение этого уравнения, определяемое равенством (6), приводится к виду у = Сх, где С— произвольная постоянная. Теперь варьируем постоянную С и ищем решение неоднородного уравнения в виде у=С(x)x. Подставляя это значение у и значение производной у'=С'(х)х+С(x) в неоднородное уравнение, получим, что С'(х)х=х2, откуда следует, что
. Общее решение этого уравнения, определяемое равенством (6), приводится к виду у = Сх, где С— произвольная постоянная. Теперь варьируем постоянную С и ищем решение неоднородного уравнения в виде у=С(x)x. Подставляя это значение у и значение производной у'=С'(х)х+С(x) в неоднородное уравнение, получим, что С'(х)х=х2, откуда следует, что 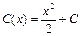 и потому
и потому 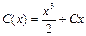 , где С – произвольная постоянная.
, где С – произвольная постоянная.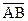 , где точки A и B обозначают соответственно начало и конец данного вектора, либо символом
, где точки A и B обозначают соответственно начало и конец данного вектора, либо символом 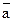 .
.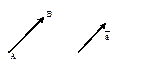
 или
или 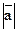 .
.