
|
|
Дифференциальные уравнения
Понятие дифференциального уравнения
Дифференциальным называется уравнение, которое кроме независимых переменных x1, х2, ..., xn и искомой функции от них y(x1, х2, ..., xn) содержит еще производные искомой функции или ее дифференциалы. Если функция, относительно которой составлено дифференциальное уравнение, зависит только от одной независимой переменной, то это уравнение называется обыкновенным дифференциальным уравнением. Если же искомая функция зависит от нескольких независимых переменных и дифференциальное уравнение содержит частные производные по этим переменным, то это уравнение называется дифференциальным уравнением с частными производными. Таким образом, для искомой функции у(х) одной независимой переменной х обыкновенное дифференциальное уравнение может быть записано в виде F(X,y,y',y",...,y(n))=0, (1) причем в частных случаях функция F может не зависеть от х, у и некоторых производных функции у(х) порядка ниже п. Наивысший порядок п производных, входящих в уравнение (1), называется порядком этого дифференциального уравнения. Дифференциальное уравнение (1) называется линейным, если его левая часть является многочленом первой степени относительно искомой функции у и ее производных у',у",...,у(n) т. е. если это уравнение имеет вид a0(x)(n) + a1(x)(n) + ... + an(X)y-f(x) = 0, (2) причем при f(x) ≡ 0 уравнение (2) называется однородным линейным уравнением порядка п, а при f(x)≡0– неоднородным линейным уравнением порядка n. Всякая n раз дифференцируемая функция у = φ(x), которая, будучи подставлена в уравнение (1), обращает его в тождество, называется решением дифференциального уравнения (1), а график любого решения называется интегральной кривой.
Дифференциальные уравнения первого порядка Общие сведения Обыкновенное дифференциальное уравнение первого порядка относительно функции у = у(х) имеет вид F(x,y,y')=0. (1) Если уравнение (1) может быть разрешено относительно производной у', то мы придем к уравнению y'=f(x,y), (2) правую часть которого естественно считать непрерывной функцией двух переменных в некоторой области G плоскости Оху. Многие вопросы теорий упрощаются, если их рассматривать для разрешенного относительно производной уравнения (2), причем к этому уравнению приводят многие прикладные задачи. Заметим, что, используя свойство инвариантности первого дифференциала, выражающееся равенством P(x,y)dx+Q(x,y)dy=0 (3) с непрерывными в некоторой области G плоскости Оху функциями Р(х,у) и Q(x,y). В уравнении (3) естественно считать обе переменные х и у равноправными и не интересоваться вопросом о том, какая из этих переменных является независимой. Обратимся к выяснению геометрического смысла уравнений (2) и (3). Рассмотрим сначала уравнение (2) и предположим, что некоторая функция у = у(х) является решением этого уравнения. Тогда в декартовой прямоугольной системе координат Оху касательная Таким образом, нахождение всех решений у = у(х) уравнения (4) геометрически приводит к следующей задаче: при условии, что в каждой точке М(х,у) некоторой области G плоскости Оху с помощью функции f(x,у) задано определенное направление, найти все кривые, которые в каждой своей точке М имеют направление, совпадающее с заранее заданным в этой точке направлением. Если функция f (x,y) из уравнения (4) непрерывна в каждой точке М(х,у) области G, то при перемещении этой точки М заданное в ней направление меняется непрерывно, и можно наглядно изобразить поле направлений, проведя в большом числе достаточно густо расположенных в области G точек короткие черточки, указывающие эти направления. Проиллюстрируем сказанное на примере рассмотрения дифференциального уравнения y'=y2 (4) Для отыскания множества всех решений этого уравнения перепишем его в виде равенства В результате получим, что Таким образом, совокупность всех решений уравнения (6) имеет вид
где С – любая постоянная.
Общим решением дифференциального уравнения (2) называют такое зависящее от произвольной постоянной С решение y = у(х, С) из которого при надлежащем выборе значения постоянной С может быть получено решение, удовлетворяющее произвольному начальному условию y(x0)=y0. Всякое решение дифференциального уравнения (2), которое получается из общего его решения при задании конкретного значения постоянной С, называется частным решением этого дифференциального уравнения. Сразу же отметим, что не существует общих методов интегрирования произвольного дифференциального уравнения первого порядка.
3.3. Уравнение первого порядка
Дифференциальное уравнение первого порядка вида f1(y)dy = f2(x)dx (1) с непрерывными функциями f1(у) и f2(x) принято называть уравнением с разделенными переменными. Если функция у=у(х) является решением этого уравнения, то при подстановке этой функции у(х) в уравнение (1) мы получим тождество, интегрирование которого дает где С – произвольная постоянная. Уравнению (2) удовлетворяют все решения уравнения (1), причем каждое решение уравнения (2) является решением уравнения (1), ибо если функция у(х) обращает в тождество уравнение (2), то, дифференцируя это тождество, мы получим, что y(x) удовлетворяет и уравнению (1). Под неопределенными интегралами, стоящими в равенстве (2), можно понимать любые первообразные функций f1 и f2, причем эти первообразные можно брать в форме интегралов с переменным верхним пределом, т. е. равенство (2) можно переписать в виде
где х0 и у0 — любые две точки, в окрестностях которых определены и непрерывны функции f2(x) и f1(y). Для получения решения дифференциального уравнения (1), удовлетворяющего произвольному начальному условию у(х0)=у0, следует положить в (3) x= х0, у = у0. При этом получим, что С = 0, и потому решение уравнения (1), удовлетворяющее начальному условию у(х0) = у0, определяется равенством
Дифференциальное уравнение вида
в котором коэффициенты при дифференциалах распадаются на произведение множителей, каждый из которых зависит только от х или только от у, называется дифференциальным уравнением с разделяющимися переменными, ибо путем деления на ψ1(y)φ2(x)это уравнение приводится к рассмотренному выше уравнению с разделенными переменными
Единственное, о чем нужно заботиться, — это возникающая при делении наψ1(y)φ2(x)возможная потеря частных решений, обращающих в нуль произведение ψ1(y)φ2(x). Впрочем, легко проверить, что в случае, если число х = а является корнем уравнения φ2(x)=0, дифференциальное уравнение (5) кроме решений, определяемых из уравнения (6), имеет дополнительное решение х = а, а в случае, если число у = b является корнем уравнения ψ1(y)=0, дифференциальное уравнение (5) имеет дополнительное решение у = b. В качестве примера рассмотрим уравнение
Разделяя переменные, получим уравнение
в котором функции (1+y2) и (1+x2) не обращаются в нуль. Поэтому все решения уравнения (7) получаются интегрированием уравнения (8) и имеет вид Эти решения можно переписать в виде ln(1+y2)=ln(1+x2)+lnC1, где С1- произвольная положительная постоянная. Окончательно получим, что 1+y2=C1(1+x2).
3.4. Однородные дифференциальные
Дифференциальные уравнения первого порядка, имеющие вид
принято называть однородными. Эти уравнения сводятся к уравнениям с разделяющимися переменными посредством замены искомой функции y(x) на новую искомую функцию Действительно, при такой замене y(x)=xu(x), y′=xu′+u, вследствие чего (1) переходит в уравнение xu′+u=f(u), которое можно переписать в виде
Интегрируя последнее уравнение, получим, что
Рассмотрим уравнение
Полагая y(x)=xu(x) и учитывая, что y′=xu′+u, приведем уравнение к виду xu′+u=u+tgu, эквивалентному Интегрируя последнее равенство и обозначая С1 произвольную положительную постоянную, получим ln|sinu|=ln|x|+lnС1, откуда следует, что sinu=C1x,т.е.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
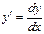 , мы можем переписать уравнение (2) в виде dy = f(x, у) dx, а в таком виде оно является частным случаем более общего уравнения
, мы можем переписать уравнение (2) в виде dy = f(x, у) dx, а в таком виде оно является частным случаем более общего уравнения и возьмем неопределенный интеграл от обеих частей этого равенства.
и возьмем неопределенный интеграл от обеих частей этого равенства.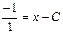 , где С – любая постоянная.
, где С – любая постоянная.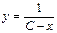 (5)
(5)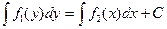 , (2)
, (2)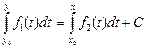 , (3)
, (3) . (4)
. (4)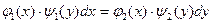 , (5)
, (5) . (6)
. (6) . (7)
. (7)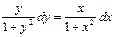 , (8)
, (8)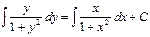
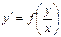 (1)
(1)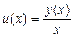 .
.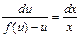
 , где С1 – произвольная положительная постоянная, так что окончательно
, где С1 – произвольная положительная постоянная, так что окончательно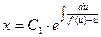 .
.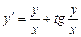
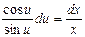 .
.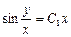 .
.