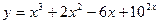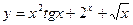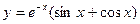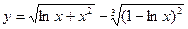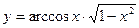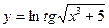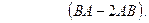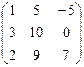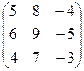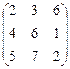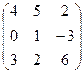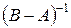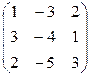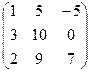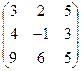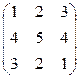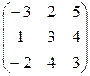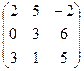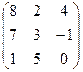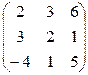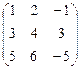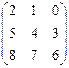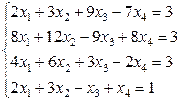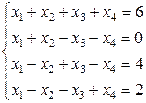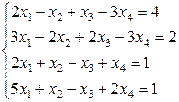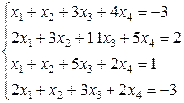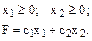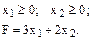|
|
Симплекс-метод решения задачи линейного программирования.Рассмотрим применение симплекс-метода на примере задачи, решенной графическим способом.
1x0-3x1-5x2=0 (0) 2x1+4x2+1x3=16 (1) 3x1+x2+1x4=9 (2)
Здесь в уравнении (0) функция F заменена на x0, а в левые части уравнений (1) и (2) добавлены фиктивные переменные x3 и x4 (x3³0, x4³0) для превращения неравенств в уравнения. Выбираем базис для начального решения. Количество переменных в базисе должно совпадать с числом уравнений, базисные переменные в системе должны присутствовать только по одному разу и коэффициенты при них равны единице. Соответственно этим условиям базисом является x0=0, x3=16 и x4=9. Тогда при этом x1=x2=0. Базисное решение совпадает с началом координат. Первая итерация. Выбираем переменную, которую будем вводить в базис. Для определения значения x2 составим таблицу.
Вводим x2=4 в уравнение (1), а x3 выведем из базиса. Пересчитываем систему уравнений. Уравнение (1) делим на 4 (коэффициент при x2). Получаем уравнение (1’): 0.5x1+1x2+0.25x3=4. (1’). Выражаем отсюда x2=4-0.5x1-0.25x3 и подставляем его в уравнения (0) и (2): 1x0-3x1-5(4-0.5x1-0.25x3)=0, 1x0-0.5x1+1.25x3=20, (0’) 3x1+4-0.5x1-0.25x3+1x4=9, 2.5x1-0.25x3+1x4=5. (2’)
Новая система уравнений имеет вид 1x0-0.5x1+1.25x3=20 (0’) 0.5x1+1x2+0.25x3=4 (1’) 2.5x1-0.25x3+1x4=5 (2’) Новый базис составляют переменные x0=20, x2=4, x4=5. При этом x1=x3=0. Это решение совпадает с (.) А. Необходима еще одна итерация, так как в уравнении (0’) коэффициент при x1 отрицателен.
Пересчитываем систему уравнений, вводя x1=2 в уравнение (2’), для чего его делим на 2.5. Получим уравнение (2”) 1x1-0.1x3+0.4x4=2. (2”) Выражаем отсюда x1=2+0.1x3-0.4x4 и подставляем его в другие уравнения: 1x0-0.5(2+0.1x3-0.4x4)+1.25x3=20, 1x0+1.2x3+0.2x4=21, (0”) 0.5x0(2+0.1x3-0.4x4)+1x2+0.25x3=4, 1x2+0.3x3-0.2x4=3, (1”) Новая система уравнений имеет вид 1x0+1.2x3+0.2x4=21, (0”) 1x2+0.3x3-0.2x4=3, (1”) 1x1-0.1x3+0.4x4=2. (2”) Новый базис составляют переменные x0=21, x2=3, x1=2, среди которых нет фиктивных. При этом x3=x4=0. Это решение совпадает с точкой B (x1=2, x2=3, F=21) и является наилучшим, так как в уравнении (0”) нет отрицательных коэффициентов при переменных x1 и x2. Задача 17 Транспортная задача. В двух пунктах отправления A1 и А2 находится соответственно 20 и 30 т горючего. В пункты В1, В2, В3 требуется доставить соответственно 15, 15 и 20 т горючего. Стоимости перевозки тонны горючего из пункта A1 в пункты В1, В2, В3 составляют соответственно 5, 4 и 1 денежных единиц, а из пункта А2 4, 3, 2 соответственно. Составить оптимальный план перевозок горючего так, чтобы общая сумма транспортных расходов была наименьшей. Решение. Построим таблицу исходных данных:
Заполнение начнем с клетки (1,1): x11=min(20,15)=15, первый столбец закрыт. Переходим к клетке (1,2): x12=min(20-15,15)=5, первая строка закрыта; далее переходим к клетке (2,2): x22=min(15-5,30)=10. Так как во второй строке оказался остаток равный 20, то переходим к заполнению клетки (2,3), куда заносим x23=20. Поскольку остатки по строке и столбцу равны нулю, опорное исходное решение построено. Этому плану соответствуют затраты в количестве F= 15×5+5×4+10×3+20×2=165 денежных единиц. Такой способ построения опорного плана называется методом Северо-Западного угла. Получив исходное опорное решение, перейдем теперь к построению новых опорных решений, улучшающих друг друга: для этого применим метод потенциалов. Припишем каждому пункту Ai некоторое число, условно равное стоимости ед. груза в этом пункте поставки ui. Соответственно каждому пункту потребления Bj припишем также некоторое число vj. Они называются потенциалами и связаны соотношением vj=ui+cij. Теперь можно приступить к попытке улучшения опорного решения. Первый этап. Если предположить, что потенциал u1=0, то можно вычислить по формуле vj=ui+cij числовые значения всех остальных. Далее следует расставить все потенциалы по соответствующим ячейкам. Второй этап. Проверяем возможности улучшения плана. Для этого анализируем незанятые клетки и по условию vj-ui£cij определяем возможности дальнейшей оптимизации опорного решения.
Если vj-ui-cij£0, то резервов оптимизации решения нет, если же vj-ui-cij>0, то план не оптимален, есть резервы и, следовательно, можно переходить к алгоритму получения нового плана. Рассмотрим пример применения метода потенциалов для оптимизации опорного решения. Пусть опорное решение имеет следующий вид:
Оценим этот план по стоимости: F=15×5+5×4+10×3+20×2=165. Рассчитаем потенциалы и внесем их в таблицу. Положим, что u1=0, тогда v1=u1+c11=0+5=5, v2=u1+c12=0+4=4, u2=v2-c22=4-3=1, v3=u2+c23=1+2=3 и таблица примет вид
Выполним проверку для незанятых ячеек условия vj-ui-cij£0. Для ячейки А1В3 получаем v3-u1-cij£0 или 3-0-1£0, т.е. условие не выполняется и, следовательно, есть резервы для улучшения плана. Для ячейки А1В3 v1-u2-c21 или 5-1-4=0 – условие выполняется, т.е. резервов для улучшения плана нет. Переместив 5 единиц продукции по циклу А1В2®А1В3®А2В3®А2В2, получим новый план:
Оценим план: F=15×5+5×1+15×3+15×2=155. Теперь выполним проверку условия vj-ui-cij£0 для ячеек А1В2 и А2В1. Для ячейки А2В1 получаем 5+1-3£0, т.е. условие не выполняется и, следовательно, есть резервы для улучшения плана. Для ячейки А1В2 или 2-4+0£0 – условие выполняется, т.е. резервов для улучшения плана нет. Перемещая 15 единиц по контуру А1В1®А1В3®А2В3®А2В1, получим новый план:
Оцениваем план: F=20×1+15×4+15×3=125. Дальнейшая проверка показывает, что условие vj-ui-cij£0 для А1В2 и А2В3 выполняется, следовательно, резервов для улучшения плана нет. Задача 18 (динамическое программирование). Производственное объединение, имеющее четыре филиала в разных городах, желает распределить ресурсы в 10 млн руб. так, чтобы получить наибольшую прибыль. Специалисты объединения изучили состояние рынка в каждой зоне и определили кривые математического ожидания прибыли как функции полных капитальных вложений:
Решение. Задача сводится к перебору всех разбиений 10 на четыре группы из целых чисел: (10,0,0,0); (9,1,0,0); (9,0,1,0); (9,0,0,1); … (8,1,1,0); (8,1,0,1); (8,0,1,1); (8,2,0,0); … и т.д. Всего 286 комбинаций. Можно вычислить доходы, соответствующие каждой комбинации, и выбрать наибольший. Таким образом, имеем комбинаторную задачу. Применим для ее решения метод динамического программирования. Обозначим функции дохода для зон 1, 2, 3 и 4 соответственно f1(x), f2(x), f3(x) и f4(x). Примем F1,2(A)– оптимальное распределение, когда А вкладывается в зоны 1 и 2 вместе; F1,2,3(A) – 1, 2 и 3 вместе; F1,2,3,4(A) – оптимальное распределение, когда А вкладывается во все четыре зоны вместе. Таким образом, чтобы определить F1,2(2), надо вычислить f1(0)+ f2(2) = 0.00+0.41=0.41; f1(1)+ f2(1)= 0.28+0.25=0.53; f1(2)+ f2(0)= 0.45+0.00=0.45, так что F1,2(A)=0.53. Вычисляем таким образом значения F1,2(0); F1,2(1); F1,2(2); F1,2(3); …; F1,2(20), что дает таблицу
Таблица позволяет определить политики, соответствующие оптимальному доходу при данных капитальных вложениях. Например, если в зоны 1 и 2 вложить 4 млн руб., то в зону 1 следует вложить 3 млн руб., а в зону 2 – 1 млн руб. Продолжим исследование поиском F1,2,3(A) , т.е. поиском оптимальной комбинации, когда капитальные вложения вкладываются в зоны 1, 2 и 3, причем
Продолжим вычисления, определяя
Можно убедиться, что те же результаты имеют место при любом ином порядке вычислений: F3,1(A), F3,1,2(A), F3,1,2,4(A) и т.п., результаты расчетов оформим в виде таблицы:
Таким образом, оптимальное распределение 10 млн руб. Интересно отметить, что попутно решены задачи оптимального распределения любого числа из 10 в две, три и четыре зоны.
Варианты заданий к контрольным работам Контрольная работа №1 Задача 1. Описать свойства функций, построить графики
Задача 2. Найти экстремумы функций одной переменной. Построить графики функций Задача 3. Найти экстремумы функции двух переменных.
Задача 4.Найти первообразные функций
Задача 5. Вычислить интеграл.
Задача 6. Аналитическая геометрия на плоскости А) Линии первого порядка
1. Построить треугольник с вершинами A(-2;4); B(2;1) и C(5;5) и определить его периметр и углы. 2. Определить середины сторон треугольника с вершинами А(-1;2), B(5;6) и С(3;0). 3. Отрезок прямой с концами в точках А(4;2) и В(13; 8), разделен на три равные части. Определить координаты точек деления. 4. Даны вершины треугольника: А(6;4), B(3;0), С(2;5). Определить длины медиан и вычислить координаты точки их пересечения. 5. Даны вершины треугольника: А(3;3), B(6;-1), С(-5;-3). Найти точку пересечения биссектрисы угла А со стороной ВС и её длину AD. 6. Дан треугольник с вершинами А(-5;0), В(2; 1), С(-2;3). Написать уравнения сторон треугольника. 7. В треугольнике с вершинами A(2;0), В(-2;6) и С(-4;2) проведены высота BD и медиана BE. Найти уравнения AC, BE и BD. 8. Найти углы и уравнения сторон треугольника с вершинами A(4;6), B(-3;0) и С(2;-3). 9. Найти точку пересечения медиан и точку пересечения высот треугольника, вершины которого A(-4;3), В(2;-4) и С(5;1). 10.Найти длину высоты AD в треугольнике с вершинами А(3;3), В(-4; 1), С(1;-2). Задача 7.Теория последовательностей и функций одной переменной. Найти пределы: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Задача 8. Дифференциальное исчисление функции одной переменной
Найти производные от функций:
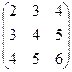
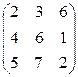
Контрольная работа №2 Задача 1. Для матриц А и В определить
Задача 2. Используя матрицы А и В, вычислить методом алгебраических дополнений
Задача 3. Решить систему уравнений методом Жордана-Гаусса. Если система является неопределенной, то в ответ записать одно базисное решение и одно частное, не являющееся базисным.
Задача 4. Решить задачу линейного программирования симплекс-методом, привести графическое решение задачи, обеспечивающее Fmax. Математическая постановка задачи в общем виде:
Конкретное задание, например, для варианта №3 имеет следующий вид:
Задача 5. Решить транспортную задачу методом потенциалов, опорный план построить методом Северо-Западного угла.
Задача 6. Динамическое программирование Распределить 8 млн. руб. между четырьмя предприятиями так, чтобы получить максимальную прибыль. Статистические исследования математического ожидания прибыли по зонам даны в следующих 10 таблицах, соответствующих разным вариантам.
Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
Вариант 5.
Вариант 6.
Вариант 7.
Вариант 8.
Вариант 9.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
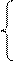 Формируем исходную систему уравнений:
Формируем исходную систему уравнений: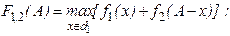
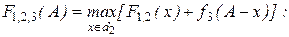
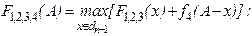
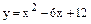

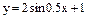

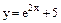

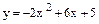
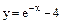

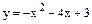

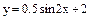


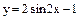
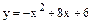


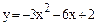

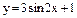

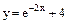
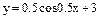


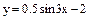


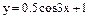
 и
и 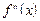 . В качестве исследуемых функций выбрать функции а и взадачи 1.
. В качестве исследуемых функций выбрать функции а и взадачи 1.
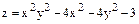
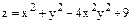



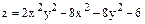


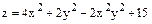
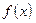


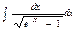
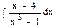
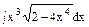
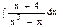
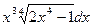


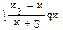





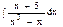

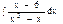

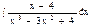
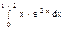

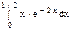
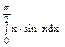




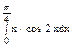

 ,
,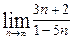 ,
, ,
, ,
,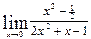 ,
,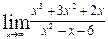 ,
,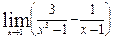 ,
, ,
, ,
, .
.