
|
|
Каноническое уравнение прямойЛюбой ненулевой вектор, параллельный данной прямой, назовем направляющим вектором этой прямой. Найдем уравнение прямой, проходящей через данную точку Точка
Это уравнение обычно называют каноническим уравнением прямой. В уравнении (5) одно из чисел l или m может равняться нулю, так как это координаты вектора. Например, уравнение оси Ox запишется так: Угол между двумя прямыми. Условия параллельности 1). Пусть прямые L1 и L2 заданы общими уравнениями
Задача об определении угла между прямыми сводится к определению угла между нормальными векторами
Условие параллельности прямых L1 и L2 эквивалентно коллинеарности их нормальных векторов
Условие перпендикулярности прямых L1 и L2 получаем из формулы (6) при cosj=0:
2). Если прямые L1 и L2 заданы каноническими уравнениями
то, рассматривая их направляющие векторы
Условие параллельности прямых L1 и L2 :
Условие перпендикулярности прямых L1 и L2 :
3). Пусть прямые L1 и L2 заданы уравнениями с угловым коэффициентом
Отсюда
Т.е. угол между прямыми L1 и L2 определяется по формуле:
Если в этой формуле поменять местами k1 и k2 , то формула определит нам угол между прямыми, смежный к прежнему углу. Так как эти два угла в сумме равны p и их тангенсы отличаются только знаком. Прямые параллельны, если tgj=0, т.е. k1=k2 . Условиеперпендикулярности прямых L1 и L2 получим из формулы (8), т.к. tgj не существует при Условие перпендикулярности прямых L1 и L2 запишем в виде:
Формула для вычисления расстояния d от точки
Кривые второго порядка Рассмотрим линии, уравнения которых в декартовой системе координат являются алгебраическими уравнениями второй степени, то есть будем рассматривать алгебраические кривые второго порядка. Будут рассмотрены три вида линий второго порядка: эллипсы, гиперболы и параболы. Основной целью является ознакомление с важнейшими геометрическими свойствами указанных линий. Эллипс Определение эллипса и вывод его канонического уравнения Эллипсом называется геометрическое место точек на плоскости, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина.
Возьмем произвольную точку М(x,y), лежащую на эллипсе. Соединим точку М с фокусами F1F2. Длины отрезков MF1 и MF2 обозначим соответственно через r1 r2: МF1=r1; MF2=r2. Числа r1 и r2 называются фокальными радиусами точки М эллипса. Учитывая, что сумма r1 и r2 есть величина постоянная (это следует из определения эллипса), обозначим: r1+r2=2a, следует 2а>2c или a>c. В противном случае либо не существует точек, удовлетворяющих поставленным требованиям, либо совокупность этих точек сводится к отрезку F1F2. На основании определения эллипса как геометрического места точек можно утверждать, что для всех точек эллипса, и только для них, должно выполняться равенство r1+r2=2a (1) Определим r1 и r2 по формулам расстояния между двумя точками:
Подставляя найденные значения r1 и r2 в уравнение (1), получим:
Уравнение (4) является уравнением эллипса. Однако полученная форма уравнения является неудобной для пользования, поэтому обычно уравнение эллипса дается в ином виде. Преобразуем уравнение (4). Пусть М(x,y) – точка эллипса, то есть равенство (4) имеет место. Преобразовав, получим:
Уравнение (5) называется каноническим уравнением эллипса, это уравнение второй степени; таким образом, эллипс есть линия второго порядка. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и имеющей заданный направляющий вектор
и имеющей заданный направляющий вектор  .
. лежит на указанной прямой тогда и только тогда, когда векторы
лежит на указанной прямой тогда и только тогда, когда векторы  коллинеарны, т.е. когда их координаты пропорциональны:
коллинеарны, т.е. когда их координаты пропорциональны: (5)
(5) .
. .
.
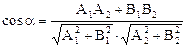 . (6)
. (6)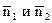 :
: .
. .
.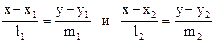 ,
, , аналогично случаю 1) имеем:
, аналогично случаю 1) имеем: . (7)
. (7) .
. . (8)
. (8) .
.
 - углы наклона прямых L1 и L2 к оси Ox, а j- один из углов между этими прямыми. Из рисунка видно, что
- углы наклона прямых L1 и L2 к оси Ox, а j- один из углов между этими прямыми. Из рисунка видно, что  .
.
 .
. (9)
(9) .
. .
. до прямой
до прямой  :
: .
. Рис.1
Рис.1
 , (2)
, (2) . (3)
. (3) . (4)
. (4)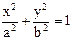 . (5)
. (5)