
|
|
Определенный интеграл, основные теоремы
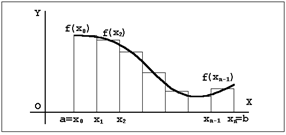
Пусть функция f(x) имеет все неотрицательные значения (см. рис. 3). Требуется вычислить площадь, ограниченную отрезком графика функции на интервале изменений аргумента от x=a до x=b.
Рис. 3 Для решения задачи разобьем рассматриваемый интервал значений аргумента на малые промежутки, ограниченные точками a=xo<x1<x2<...xn=b. Естественно считать, что на каждом промежутке от xk-1 до xk значение функции f(x) меняется мало. Поэтому приближенно значение функции на указанном промежутке можно считать постоянным и равным, например, f(xk). В таком случае площадь, ограниченная функцией f(x) на промежутке изменения аргумента ∆xk=xk -xk-1, приближенно равна f(xk)∆xk, а полная площадь aSb на интервале от a до b приблизительно равна aSb ≈ f(x1)∆x1 + f(x2)∆x2 + ... + f(xn)∆xn. Естественно ожидать, что при уменьшении всех промежутков ∆xk мы будем получать все более и более точное значение площади aSb. Точное значение площади мы получим, перейдя в сумме к пределу при стремлении всех ∆xk к нулю (при этом количество слагаемых будет возрастать). Употребляя символ предела, мы можем записать следующую формулу: aSb = lim∆xk→0 {f(x1)∆x1 + f(x2)∆x2 + ... + f(xn)∆xn}. В математике предел данной суммы называется определенным интегралом от функции f(x) в пределах от a до b и обозначается символом
Приближенная сумма представляет собой сумму площадей прямоугольников, основаниями которых служат отрезки ∆xk, а высотами – f(∆xk). Иными словами, эта сумма равна площади изображенной на рис.3 ступенчатой фигуры. Естественно ожидать, что при стремлении к нулю длин всех отрезков ∆xk площадь указанной ступенчатой фигуры будет стремиться к площади заштрихованной фигуры, лежащей под графиком функции y = f(x) на отрезке от a до b. Эту криволинейную фигуру часто называют криволинейной трапецией. Таким образом, определенный интеграл равен площади указанной криволинейной трапеции.
Рис. 4 Обозначим через F(x) определенный интеграл от функции f(x) в пределах от a до x, т.е. положим
С геометрической точки зрения этот интеграл равен площади криволинейной трапеции, лежащей под графиком функции y=f(x) на отрезке от a до x. Используя наглядные геометрические соображения, покажем, что введенная функция F(x) является одной из первообразных функции f(x), т.е. убедимся в том, что F'(x) = f(x). Пусть ∆x – некоторое приращение аргумента x. Очевидно, что разность F(x+∆x) - F(x) равна площади заштрихованной "узкой" криволинейной трапеции на рис.4. Площадь этой трапеции при малом ∆x мало отличается от площади f(x)∆x прямоугольника с основанием ∆x и высотой f(x). Отсюда ясно, что при малом ∆x отношение {F(x+∆x) - F(x)}/ ∆x мало отличается от высоты f(x) указанного выше прямоугольника. Так как предел при ∆x→0 данной дроби равен производной F'(x), то F'(x)=f(x). Итак, функция F(x) является одной из первообразных функции f(x). Следовательно, любая первообразная Ф(x) функции f(x) имеет вид
Уточним теперь с помощью этой формулы связь между определенным интегралом a∫bf(x)dx и любой первообразной Ф(x) функции f(x). Полагая в формуле последовательно x=a и x=b и учитывая очевидное из наглядных геометрических соображений равенство
получим
Поэтому
Данная формула является одной из основных формул интегрального исчисления и называется формулой Ньютона-Лейбница. Рассмотрим основные теоремы интегрирования. 1. 2. Перестановка пределов интегрирования: если существует 3. Теорема о разбиении интеграла. Если существуют интегралы 4. Если существует 5. Если существуют интегралы 6. Первая теорема о среднем значении. Если f(x) интегрируема на [a, b] и m≤f(x)≤M, то существует число μ, m≤μ≤M, такое, что 7. Вторая теорема о среднем значении. Если f(x) монотонна и ограничена, а g(x) интегрируема, то на [a, b] существует такая точка ξ, что Важным частным случаем определенного интеграла является несобственный интеграл, у которого один из пределов представляет собой бесконечность.
Способы интегрирования
1. Замена переменной под знаком определенного интеграла. Пусть выполнены следующие условия: 1) функция f(x) непрерывна на интервале [a,b]; 2) интервал [a,b] является множеством значений некоторой функции x=g(t), определенной на интервале α≤t≤β и имеющей на этом интервале непрерывную производную; 3) g(α)=a, g(β)=b. При этих условиях справедлива формула
Формула показывает, что если вычислен интеграл, стоящий в левой части этой формулы, то вычислен и интеграл, стоящий в правой части, и наоборот. Указанная формула называется формулой замены переменной под знаком определенного интеграла. Рассмотрим некоторую первообразную Ф(x) функции f(x). По формуле Ньютона-Лейбница имеем
Так как функции Ф(x) и x=g(t) дифференцируемы на соответствующих сегментах, то сложная функция Ф(g(t)) дифференцируема на интервале [α,β]. Поэтому, применяя правило дифференцирования функции, получим
Причем производная Ф' вычисляется по аргументу x: Ф'(g(t))=Ф`(x), где x=g(t). Поскольку Ф'(x)=f(x), то при x=g(t) получим Ф`(g(t))=f(g(t)). Подставляя это значение Ф'(g(t)) в правую часть равенства, получим
Следовательно, функция Ф(g(t)), определенная и непрерывная на интервале [α,β], является на этом интервале первообразной для функции (g(t))g’(t), и поэтому, согласно формуле Ньютона-Лейбница,
Так как g(β)=b, а g(α)=a, то
Сравнивая последнюю формулу с формулой из нашего утверждения, мы убеждаемся в ее справедливости. 2. Формула интегрирования по частям. Пусть функции u(x) и v(x) имеют непрерывные производные на сегменте [a,b]. Тогда имеет место следующая формула интегрирования по частям для определенных интегралов:
Так как v`(x)dx=dv и u`(x)dx=du, то эту формулу записывают еще следующим образом:
В справедливости этих формул убедиться нетрудно. Действительно, функция u(x)v(x) является первообразной для функции u(x)v’(x)+v(x)u’(x). Поэтому в силу формулы Ньютона-Лейбница:
Отсюда, используя свойства определенных интегралов, можно убедиться в справедливости нашего утверждения. 3. Интегрирование рациональной дроби. Интегрировать многочлены мы умеем (напомним, что неопределенный интеграл от многочлена представляет собой некоторый многочлен степени, на единицу более высокой). Остается научиться интегрировать правильную рациональную дробь, поскольку неправильная сводится к правильной + многочлен. Проблема интегрирования сводится к интегрированию простейших дробей следующих четырех типов:
Здесь β=2, 3, …; λ=2, 3, …; B, M, N, b, p и q – некоторые вещественные числа, причем трехчлен x2+px+q не имеет вещественных корней, т.е. q-p2/4>0. Справедлива следующая теорема: всякая рациональная дробь интегрируема в элементарных функциях. Действительно, дроби первого и второго типа интегрируемы в элементарных функциях при помощи подстановки: t=x-b.
Если квадратные трехчлены третьей и четвертой дробей представить в виде (x2+px+q)=(x+p/2)2+(q-p2/4) и, учитывая, что (q-p2/4)>0, ввести в рассмотрение вещественную постоянную

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
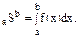


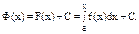
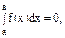
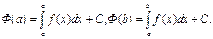
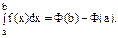
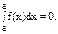
 при a<b, то существует
при a<b, то существует 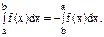
 и
и  , то существует также
, то существует также  и для любого взаимного расположения точек a, b, c:
и для любого взаимного расположения точек a, b, c:  =
=  .
. , то существует также
, то существует также  и
и  .
. В частности, если f(x) непрерывна на [a, b], то существует число ξ, a<ξ<b, такое, что
В частности, если f(x) непрерывна на [a, b], то существует число ξ, a<ξ<b, такое, что 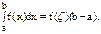
 =
=  +
+  .
.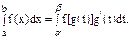
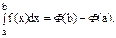
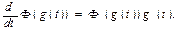
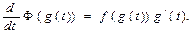
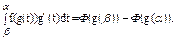
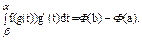

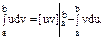
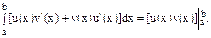
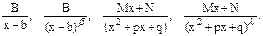
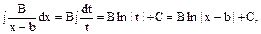
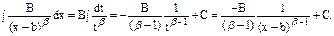
 , а затем сделать подстановку t=x+p/2, то проблема интегрирования может быть решена с использованием известных формул интегрирования.
, а затем сделать подстановку t=x+p/2, то проблема интегрирования может быть решена с использованием известных формул интегрирования.