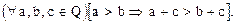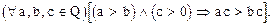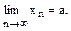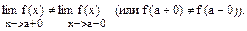|
|
Прямое произведение двух множествПусть имеются два множества А и В и пусть аÎА, bÎB. Совокупность всевозможных упорядоченных пар (а,b) составляет новое множество, называемое прямым произведением А и В. Прямое произведение обозначается А´В.
Вещественные числа и их изображение на числовой оси. Основные свойства рациональных чисел Основным понятием математики являются числа натурального ряда:
Целые числа: Рациональным числом называется число, представимое в виде отношения двух целых чисел Отметим при этом, что одно и то же рациональное число представимо в виде отношения различных целых чисел
В курсе элементарной математики вводились определения операций сложения и умножения рациональных чисел, давалось правило сравнения этих чисел, доказывались простейшие свойства. Поэтому перечислим без доказательства основные свойства рациональных чисел, вытекающие из соответствующих свойств целых чисел. Главную роль среди свойств играют три правила: - правило сравнения; - правило образования сумм; - правило образования произведения. I. Правило сравнения: любые два рациональные числа а и b связаны одним и только одним из трех знаков >, <, =, причем если а>b, то b< а. Правило сравнения рациональных чисел формулируется так: два неотрицательных рациональных числа Правило сравнения обладает следующим свойством: 1. (из а>b и b>с)Þ а>с (свойство транзитивности знака >); (из а=b и b=с)Þ а=с (свойство транзитивности знака =). II. Правило образования сумм. Существует правило, посредством которого любым двум рациональным числам а и b ставится в соответствие определенное рациональное число с, называемое их суммой и обозначаемое символом с=а+b. Правило образования суммы рациональных чисел Правило сложения рациональных чисел обладает следующими свойствами: 2. а+b=b+а (коммутативность, или переместительное свойство); 3.(а+b)+c=а+(b+c) (ассоциативность, или сочетательное свойство); 4. 5. III. Правило образования произведения. Существует правило, посредством которого любым двум рациональным числам а и b ставится в соответствие определенное рациональное число с, называемое их произведением и обозначаемое символом с=аb. Правило образования произведения рациональных чисел
Операция нахождения произведения называется умножением. Свойства правила умножения рациональных чисел: 6. 7. 8. 9. Свойство, связывающее правила сложения и умножения: 10. Свойства, связывающие знак > со знаком сложения и умножения: 11. 12. Последнее свойство, называемое аксиомой Архимеда, формулируется следующим образом. Каково бы ни было рациональное число а, можно число 1 повторить слагаемым столько раз, что полученная сумма превзойдет а. Из вышеперечисленных основных свойств рациональных чисел могут быть получены как следствие все другие алгебраические свойства этих чисел, относящиеся как к арифметическим действиям, так и к сочетанию равенств и неравенств.
2.2. Основные свойства и графики
Математика изучает количественные отношения и пространственные формы окружающего нас мира. Элементарная математика имеет дело в основном спостоянными величинами и простейшими геометрическими фигурами (треугольниками, окружностями и т.п.). Понятий и методов элементарной математики оказывается недостаточно для описания процессов, зависящих от времени или каких-либо других параметров. Со всяким процессом связано представление о переменной величине, т.е. о такой величине, которая в условиях данного процесса принимает различные значения. Более того, всякий процесс характеризуется, по меньшей мере, двумя переменными величинами, изменение которых взаимосвязано. Такого рода зависимости между двумя переменными x и y, при которых каждому значению переменной x ставится в соответствие определенное значение y, встречаются при рассмотрении процессов различной природы: от движения физических тел до сложных социально-экономических явлений. Абстрагируясь от конкретного содержания переменных x и y, мы приходим к одному из важнейших математических понятий - понятию функции. Определение. Если известно правило, посредством которого каждому значению переменной x ставится в соответствие определенное значение переменной y, то говорят, что переменная y является функцией переменной x. При этом переменная x называется аргументом рассматриваемой функции, а соответствующее данному x значение переменной y называется частным значением функции в точке x. Для обозначения функции используются следующие символы: y=φ(x) или y=f(x). Такой способ задания функции при помощи формулы называется аналитическим. Наряду с этим способом существуют и другие способы задания функции. В практике сбора информации, в различных социологических опросах и научных экспериментах весьма распространен табличный способ задания функции, при котором значения аргумента и соответствующие им значения функции выписываются в виде таблицы. Часто зависимость между аргументом и функцией задается посредством графика, например ЭКГ (электрокардиограмма). Такой способ задания функции называется графическим. Потребности теории и практики иногда приводят к необходимости изучения функции y=f(x), аргумент x которой сам по себе представляет некоторую функцию x=φ(t) нового аргумента t. Основными элементарными функциями называются следующие функции: xp (степенная), ax (показательная), ех (экспоненциальная), 1/х (гиперболическая), k/х (обратная), logax (логарифмическая), тригонометрические: cosx, sinx, tgx.
2.3. Предел функции, непрерывность функции,
Постоянная величина a называется пределом переменной x, если для любого наперед заданного сколь угодно малого положительного числа ε можно указать такой момент в процессе изменения x, что все последующие значения переменной x будут удовлетворять неравенству |x-a|<ε. Из курса элементарной математики студент имеет представление о числовых последовательностях, примерами которых могут служить члены арифметической и геометрической прогрессии. Определение. Постоянная величина a называется пределом последовательности xn, если для каждого положительного наперед заданного сколь угодно малого числа ε существует такой номер N, что все значения xn , у которых номер n>N, удовлетворяют неравенству | xn-a| <ε. Говорят, что последовательность сходится к a. Обозначается этот предел следующим образом:
Введем теперь понятие предела функции. Пусть функция y=f(x) определена в некоторой окрестности точки x0. Определение. Постоянная величина A называется пределом функции f(x) в точке x0, если для каждого положительного наперед заданного сколь угодно малого числа ε >0 найдется такое положительное число δ >0, что для всех x, отличных от x0 и удовлетворяющих неравенству |x- x0|< δ, выполняется неравенство |f(x)-A|< ε . Когда число A есть предел функции f(x) в точке x0, принято обозначение A=limx →x0f(x). Сформулируем теоремы о пределах функций, полезные при решении задач на вычисление пределов. Теоремы. Если существуют limx→x0f(x) и limx→x0g(x), то 1) limx→x0[f(x)±g(x)] = limx →x0f(x)± limx →x0g(x); 2) limx →x0kf(x) = k limx →x0f(x); 3) limx →x0f(x)g(x) = limx →x0f(x)limx →x0g(x); 4) limx →x0[f(x):g(x)] = limx →x0f(x):limx →x0f(x), если 5) limx →x0[f(x)]n = [limx →x0f(x)]n; 6) limx →x0C = C, где С = const. Понятие предела функции в точке позволяет описать важнейшее свойство некоторых функций – свойство непрерывности. Так, часто говорят о непрерывно изменяющейся температуре, непрерывно текущем времени и т.п., понимая под этим постепенное изменение указанных переменных. Для функции это означает, что малое изменение аргумента вызывает малое изменение функции. Дадим точное определение непрерывности. Пусть функция y=f(x) определена в точке x=x0 и ее окрестности. Придадим аргументу новое значение, полагая x=x0+∆x. Тогда функция y примет соответствующее значение f(x0+∆x). Разность ∆y = f(x0+∆x) - f(x0) будем называть приращением функции y=f(x) в точке x=x0; величина ∆x = x- x0 называется приращением аргумента. Определение. Если бесконечно малому приращению ∆x аргумента в точке x0 соответствует бесконечно малое приращение ∆y данной функции, то функцию y=f(x) называют непрерывной в точке x0, т.е.
Если функция непрерывна в каждой точке некоторого промежутка (a,b), то ее называют непрерывной во всем промежутке (a,b). Существуют следующие типы точек разрыва функции: · Устранимый разрыв 1-го рода. Точка а называется точкой устранимого разрыва первого рода функции у= f(х), если предельное значение функции в этой точке существует, но в точке а функция f(x) или не определена, или ее частное значение f(a) в точке а не равно предельному значению. · Неустранимый разрыв 1-го рода. Точка а называется точкой неустранимого разрыва 1-го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу правое и левое предельные значения:
· Разрыв 2-го рода. Точка а называется точкой разрыва Другим полезным классом функций являются функции нескольких переменных. Дадим определение функции двух переменных. Определение.Если каждой паре значений (x,y) соответствует единственное значение z, то переменную z называют функцией от двух независимых переменных x и y, или аппликатой, и обозначают так: z=f(x,y). Пусть y=f(x) представляет собой закон взаимосвязи двух переменных. Нас может заинтересовать вопрос, как в среднем изменится величина y при изменении х от x до x+∆x, где x - некоторое фиксированное значение аргумента, а ∆x - некоторое его приращение. Очевидно, что ∆y=f(x+∆x)-f(x) и будет приращением функции y при соответствующем приращении ∆x. Тогда средняя скорость, изменения функции за данное приращение аргумента будет равна Vcp = ∆y/∆x = {f(x+∆x)-f(x)}/∆x. Поскольку значение x фиксировано, то из последней формулы видно, что Vcp является функцией аргумента ∆x. Если уменьшать ∆x, то мы будем получать все более точное значение скорости изменения функции y в зависимости от изменения ее аргумента в точке x и достигнем точного значения при стремлении ∆x к нулю (∆x→0). Таким образом, мы приходим к понятию производной. Итак, производной функции y=f(x) в фиксированной точке мы будем называть предел, к которому стремится дробь ∆y/∆x = {f(x+∆x)-f(x)}/∆x при ∆x, стремящемся к нулю. Операцию нахождения производной принято называть дифференцированием. Используя известные символы для обозначения предела и производной, можно записать f'(x) = lim∆x→0∆y/∆x = lim∆x→0 {f(x+∆x)-f(x)}/∆x. Приведем таблицу производных некоторых элементарных функций:
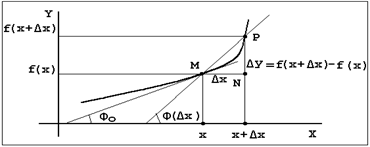
Для вычисления производных широкого класса функций следует присоединить к указанной выше таблице производных правило дифференцирования сложной функции, а также правила дифференцирования суммы, разности, произведения и частного функций. Сформулируем правило дифференцирования сложной функции y=f(x), где x=φ(t). Для нахождения производной y'(t) сложной функции y=f{φ(t)} по аргументу t в данной точке t следует: 1) вычислить производную φ'(t) функции x=φ(t) в точке t; 2) вычислить производную f'(x) функции у=f(x) в точке x, где x=φ(t); 3) перемножить указанные производные. Таким образом, производная сложной функции y=f{φ(t)} может быть найдена по формуле y'(t)=f'(x)φ'(t). Приведем теперь правила дифференцирования суммы, разности, произведения и частного (в предположении, что u(x) и v(x) имеют производные): [u(x)±v(x)]' = u'(x) ±v'(x), [u(x)v(x)]' = u(x)v'(x) + u'(x)v(x), [u(x)/v(x)]' = {u'(x)v(x) - u(x)v'(x)}/v2(x). Сформулированные выше правила дифференцирования и таблица производных представляют собой основной аппарат той части математического анализа, которую обычно называют дифференциальным исчислением. Необходимо также добавить, что производная функции может являться в свою очередь непрерывной и дифференцируемой функцией в некотором промежутке. Тогда можно ввести понятие производной второго порядка f''(x) как производной от производной, т.е. f''(x) = {f'(x)}' = limΔx→0{f'(x+∆x) - f'(x)}/ ∆x. Аналогично для производных 3-го, 4-го и т.д. n-го порядка. Выясним геометрический смысл производной. С этой целью рассмотрим график функции y=f(x). Пусть точка M на графике функции соответствует фиксированному значению аргумента x, а точка P – значению x+∆x, где ∆x – некоторое приращение аргумента. Прямую MP будем называть секущей. Обозначим через φ (∆x) угол, который образует эта секущая с осью Ox (очевидно, что этот угол зависит от ∆x). Касательной к графику функции y=f(x) в точке M будем называть предельное положение секущей MP при стремлении точки P к точке M по графику (или при ∆x→0). Из рис. 1 ясно, что tgφ(∆x) = PN/MN = ∆y/∆x = {f(x+∆x) - f(x)}/∆x. Так как при ∆x→0 секущая MP переходит в касательную, то lim∆x→0tgφ(∆x) = tg φ0, где φ0 - угол, который образует касательная с осью Ox. С другой стороны, lim∆x→0tgφ(∆x) = lim∆x→0{f(x+∆x) - f(x)}/∆x = f'(x).
Рис. 1. Следовательно, f'(x) = tg φ0. Тангенс угла наклона прямой к оси Ox называют угловым коэффициентом этой прямой. Таким образом, производная f'(x) равна угловому коэффициенту касательной к графику функции y=f(x) в точке M. Физический смысл производной функции в данной точке означает мгновенную скорость изменения функции в этой точке. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 которые появились в результате счета предметов.
которые появились в результате счета предметов.
 (q¹0; p и q - целые числа).
(q¹0; p и q - целые числа).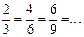 . Множество всех рациональных чисел будем обозначать через Q, тогда
. Множество всех рациональных чисел будем обозначать через Q, тогда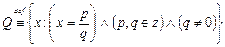

 ; два неположительных рациональных числа а и b связаны тем же знаком, что и два неотрицательных числа |b| и |а| ; если а - неотрицательное, а b - отрицательное число, то а>b.
; два неположительных рациональных числа а и b связаны тем же знаком, что и два неотрицательных числа |b| и |а| ; если а - неотрицательное, а b - отрицательное число, то а>b. определяется формулой
определяется формулой  . Операция нахождения суммы называется сложением.
. Операция нахождения суммы называется сложением. (особая роль нуля);
(особая роль нуля); ; число а1 называется противоположным для числа а.
; число а1 называется противоположным для числа а. определяется формулой
определяется формулой  .
. (переместительное свойство);
(переместительное свойство); (сочетательное свойство);
(сочетательное свойство); (особая роль единицы);
(особая роль единицы); рациональное число
рациональное число  называется обратным рациональному числу а.
называется обратным рациональному числу а. (распределительное свойство умножения относительно суммы).
(распределительное свойство умножения относительно суммы).