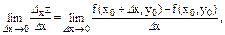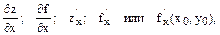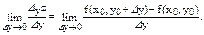|
|
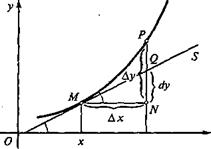
Понятие дифференциала функцииПусть функция у =f(х) дифференцируема в точке х, т.е. ее приращение в этой точке может быть записано в виде выражения Δy=AΔx+αΔх (1), представляющего собой сумму двух слагаемых: первое из этих слагаемых АΔx при А≠0 — это функция приращения аргумента Δх, линейная и однородная относительно Δх; это слагаемое представляет собой при Δх→ 0 бесконечно малую такого же порядка, что и Δx; второе слагаемое αΔх является при Δx→0 бесконечно малой более высокого порядка, чем Δх, так как отношение Итак, в случае A≠0 дифференциалом функции у =f(х) в данной точке х, соответствующим приращению аргумента Δх, называют главную линейную относительно Δх часть приращения этой функции в точке х. Дифференциал функции обозначается символом dy. Если для приращения функции Δу справедливо представление (1), то дифференциал этой функции, по определению, равен dy=AΔx. (2) В случае A = 0 дифференциал функции также определяется формулой (2), т.е. считают, что в этом случае он равен нулю. Учитывая теорему дифференцируемости функции в данной точке, формулу (2) можно переписать в виде dy=f'(x) Δx. (3) Подчеркнем, что дифференциал функции dy в данной точке х, вообще говоря, не равен приращению функции Δу в этой точке. Рассмотрим график функции у=f(х) (рис. 2).
Рис. 2 Пусть точка М на кривой у =f (x) соответствует значению аргумента х, точка Р на той же кривой соответствует значению аргумента х+Δх, MS— касательная к кривой у =f(х) в точке М. Пусть, далее, прямая MN параллельна Ох, прямая PN параллельна Оу, Q — точка пересечения касательной MS с прямой PN. Тогда приращение функции Δу равно величине отрезка NP. В то же время из прямоугольного треугольника MQN и из формулы (3) ясно, что дифференциал функции dy равен величине отрезка NQ, ибо величина отрезка MN равна Δх, атангенс угла <QMN равен f'(x). Очевидно, что величины отрезков NP и NQ, вообще говоря, различны. Установим выражение для дифференциала функции у =f(х), аргумент х которой является независимой переменной. Под дифференциалом dx независимой переменной х можно понимать любое (не зависящее от х) число. Договоримся в дальнейшем брать это число равным приращению Δх независимой переменной, что позволяет нам переписать формулу (3) в виде dy=f '(x)dx. (4)
Введем понятие дифференциала dх независимой переменной х, под которым можно понимать любое (не зависящее от х) число. Договоримся в дальнейшем брать это число равным приращению ∆х независимой переменной, что позволяет переписать формулу для дифференциала функции в виде dy=f '(x)dx. На основании этой формулы мы можем сделать вывод: для случая, когда аргумент x функции y=f(x) является независимой переменной, производная f'(x) этой функции равна отношению дифференциала функции dy к дифференциалу аргумента dx, т.е. f '(x)=dy/dx. Рассмотрим некоторые понятия и определения, касающиеся дифференцирования функций нескольких переменных. Пусть дана функция z=f(x, y), определенная на некотором множестве пар значений переменных x и y. Это множество можно наглядно представить как область плоскости, а пару значений – как точку этой области. Так как x и y – независимые переменные, то одна из них может изменяться, а другая – сохранять свою величину. Возьмем точку N0(x0,y0) и дадим x0 приращение ∆x, оставляя y0 постоянным. Тогда функция z=f(x,y) получит приращение, зависящее только от изменения x: ∆xz =f(x0+∆x,y0)-f(x0,y0), которое называют частным приращением функции по x. Аналогично определяется частное приращение по y: ∆yz =f(x0,y0+∆y)- f(x0,y0). Определение. Если существует конечный предел
то его называют частной производной функции z=f(x,y) по x в точке (x0,y0). Если такой предел можно найти в каждой точке области, то говорят, что функция z=f(x,y) имеет частную производную по x в этой области. Обозначают частную производную одним из следующих способов:
если требуется указать точку, где вычисляется производная. Аналогично: частной производной функции f(x,y) в точке (x0,y0) по y называется следующий предел:
Это определение можно распространить и на случай функции большего числа переменных. Вообще частной производной функции нескольких переменных называется производная, вычисленная в предположении, что изменяется лишь один из аргументов, а остальные – постоянны. В обозначениях указывают, какой из аргументов изменяется. Пример. Найти частные производные функции z=ax2+2bxy+cy2. Чтобы найти частную производную z'x, будем считать Дифференциал функции двух переменных dz = z'xdx + z'ydy. Пример. Для приведенного выше примера дифференциал будет выглядеть: dz = (2ax+2by=2(ax+by))dx + 2bx+2cy=2(bx+cy)dy.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
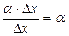 стремится к нулю при Δх→0. Таким образом, при А≠0 первое слагаемое АΔx является главной частью приращения дифференцируемой функции. Эту главную часть приращения называют дифференциалом функции в точке х, соответствующим приращению аргумента Δx.
стремится к нулю при Δх→0. Таким образом, при А≠0 первое слагаемое АΔx является главной частью приращения дифференцируемой функции. Эту главную часть приращения называют дифференциалом функции в точке х, соответствующим приращению аргумента Δx.