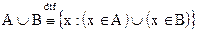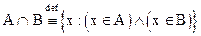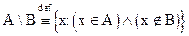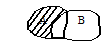|
|
Отрицание высказываний, содержащих кванторыКафедра информационных технологий
Математика
Математический анализ
Учебно-методическое пособие
Ростов-на-Дону, 2008
Т 81 Тугуз Ю.Р Математика. Математический анализ и линейная алгебра: Учебно-метод.ическое пособие. Ростов н/Д, 2008. – 164 с.
В учебно-методическое пособие включены основные теоретические положения математического анализа, аналитической геометрии, линейной алгебры, дифференциальных уравнений, математической экономики и методов оптимизации, методические указания по их изучению, а также задачи и примеры решения. Пособие составлено в соответствии с образовательными стандартами специальностей «Государственное и муниципальное управление», «Менеджмент организации», «Налоги и налогообложение» и «Юриспруденция» и рекомендуется студентам всех форм обучения.
Печатается по решению кафедры.
© Тугуз Ю.Р., 2008
Оглавление 1. Общие методические указания 2. Основные теоретические положения 2.1. Теория множеств. 7 2.2. Основные свойства и графики элементарных функций.. 13 2.3. Предел функции, непрерывность функции, 2.4. Анализ функций одной и двух переменных. 21 2.5. Интегрирование функций.. 23 2.6. Определенный интеграл, основные теоремы.. 25 2.7. Способы интегрирования. 28 3. Дифференциальные уравнения………………………………………30 3.1. Понятие дифференциального уравнения. 30 3.2. Дифференциальные уравнения первого порядка. 31 3.3. Уравнение первого порядка 3.4. Однородные дифференциальные уравнения 3.5. Линейное уравнение первого порядка. 35 4. Векторная алгебра………………………………………………………….38 4.1. Понятие вектора и линейные операции над векторами.. 38 4.2. Скалярное произведение двух векторов. 48 4.3. Векторное произведение двух векторов. 51 4.4. Смешанное произведение трех векторов. 56 5. Аналитическая геометрия на плоскости………………………..58 5.1.............................. Различные виды уравнений прямой на плоскости.. 58 5.2. Кривые второго порядка. 62 5.3. Аналитическая геометрия в пространстве. 78
6. Линейная алгебра…………………………………………………………...94 6.1. Матрицы. Основные определения. 94 6.2. Действия над матрицами.. 95 6.3. Обратная матрица. 98 6.4. Системы линейных уравнений.. 99 7. Задачи оптимизации……………………………………………………..107 7.1. Математические модели оптимизации.. 107 7.2. Задачи линейного программирования. 109 7.3. Задачи динамического программирования. 114 8. Примеры решения типовых задач…………………………………116 9. Варианты заданий к контрольным работам………………….140 9.1. Контрольная работа №1. 140 9.2. Контрольная работа №2. 144 10. Задачи для самостоятельной работы………………………...153 11. Вопросы к зачету………………………………………………………...161 12. Вопросы К экзамену……………………………………………………162 Литература……………………………………………………………………….163 1. Общие методические указания Курс «Математический анализ и линейная алгебра» согласно стандартам специальностей «Государственное и муниципальное управление» и «Менеджмент организации» относится к федеральному компоненту общих математических и естественнонаучных дисциплин и содержит следующие разделы: · математический анализ; · линейная алгебра; · методы оптимизации; · аналитическая геометрия; · дифференциальные уравнения; · математическая экономика. Дисциплина «Математический анализ и линейная алгебра» базируется на школьной программе и имеет связь с параллельно изучаемыми дисциплинами (статистика, информатика, экономическая теория и др.). Знания, полученные при изучении курса математики, используются в следующих дисциплинах: маркетинг, бизнес-планирование, рынок ценных бумаг, теория управления, предпринимательство, разработка управленческих решений, информационные технологии управления и др., а также при выполнении курсовых и дипломных работ. Для изучения курса математики необходимы знания следующих разделов школьной программы: · числовые последовательности, арифметическая и геометрическая прогрессии; · элементарные алгебраические функции, их свойства и графики, линейные преобразования над ними; · производная функции и основные правила дифференцирования; · неопределенный и определенный интегралы; · системы линейных уравнений и неравенств и способы их решения. В результате изучения курса «Математический анализ и линейная алгебра» студенты должны: знатьосновные теоретические положения курса и уметь решать типовые задачи. Для закрепления практических навыков решения задач по математическому анализу и линейной алгебре для студентов заочной формы обучения учебным планом предусмотрены первая и вторая контрольные работы, включающие следующие типовые задачи: · описание свойств функции и построение графиков; · анализ функции одной переменной; · нахождение экстремумов функции двух переменных; · нахождение первообразной функции и вычисление интеграла; · решение системы алгебраических линейных уравнений · решение системы алгебраических линейных уравнений · решение системы алгебраических линейных уравнений методом Гаусса; · решение задачи линейного программирования симплекс-методом; · решение транспортной задачи методом потенциалов; · решение задачи методом динамического программирования; · решение дифференциальных уравнений. Контрольные работы для студентов заочной формы обучения должны быть выполнены в отдельных тетрадях, на обложках которых студенту следует указать: группу и год обучения, фамилию, имя и отчество; номер контрольной, номер варианта; дату выполнения и полный домашний адрес с почтовым индексом. Студент выполняет вариант контрольной работы, соответствующий последней цифре номера зачетной книжки или последней цифре порядкового номера в списке группы. Решения всех задач и пояснения к ним должны быть достаточно подробными. Все вычисления необходимо приводить полностью, с требуемой точностью либо представлять их в виде таблицы. Графики следует оформлять аккуратно, в соответствии с общепринятыми требованиями. В конце контрольной работы нужно указать список используемой литературы и поставить личную подпись. Для замечаний преподавателя необходимо на каждой странице оставлять поля. Поступившие на проверку контрольные работы рецензируются преподавателем. Работа считается зачтенной, если содержит правильные решения всех задач и защищена студентом. Неправильно выполненные работы возвращаются студентам для доработки. Студент допускается к сдаче зачета и экзамена при успешном выполнении и защите соответствующих контрольных работ. 2. Основные теоретические положения
Теория множеств Основные понятия Множество есть исходное, начальное (а, следовательно, и неопределяемое) понятие. Можно лишь сказать, что множество есть собрание объектов, при этом не будем уточнять, какие собрания объектов являются множествами. Объекты этого собрания называются элементами множества. Множества, состоящие из конечного числа элементов, называются конечными множествами. Если множество состоит из n элементов, то это обозначают следующим образом:
Часто приходится сталкиваться с другими, неконечными, или, как принято говорить, бесконечными множествами. Таковы, например, множества всех натуральных чисел, всех нечетных чисел и т.д. К числу конечных множеств мы будем относить и пустое множество, т.е. множество, не содержащее ни одного элемента; число элементов пустого множества есть нуль. Такое множество обозначим символом Æ. Если элемент x принадлежит множеству А, то пишут xÎA. Запись Запись AÍB (или BÊA) означает, что каждый элемент множества А является элементом множества В или, другими словами, множество А есть подмножество множеств В (или множество А включено в множество В). Два множества называются равными, если они состоят из одних и тех же элементов: запись А=В. Если А есть подмножество В, причем множество А не совпадает с множеством В, то пишут A Ì B или B É A. Если множество А не принадлежит множеству В, то пишут Разберем некоторые понятия математической логики. Прежде всего, что такое математическая логика? Математическая логика – наука о законах логического вывода. В математической логике под предложением понимают то же самое, что вкладывают в смысл этого термина в грамматике любого естественного языка. Высказыванием называется предложение, о котором имеет смысл говорить, что оно истинно или ложно. Каждое высказывание либо истинно, либо ложно. Истинному высказыванию будем ставить в соответствие единицу, а ложному – логический ноль (1;0). Пример: (10=15)=0 (высказывание “10 равно 15” - ложно) (5>-1)=1 (высказывание “5 больше -1” - истинно). Будем обозначать высказывания буквами какого-либо алфавита: X, Y,L,.........; А, В,...... Высказывательная форма – это выражение, содержащее одну или несколько переменных и становящееся высказыванием при подстановке чисел или элементов каких-либо множеств вместо своих переменных.
Кванторы Иногда удобно представить некоторые словесные выражения посредством символов. " - каково бы ни было, для любого (квантор всеобщности). $ - существует (квантор существования).
Символом “:” будем обозначать следующую группу слов: “такое, что”, “удовлетворяет условию”, “выполняется”. Отрицание высказываний, содержащих кванторы Отрицание под знаком " или $ превращает его, соответственно, в знак $ или " и переносится на свойство, стоящее после двоеточия. Пример 1. Пусть имеем высказывание: ("xÎA): x £ x (для любого x из множества А имеет место неравенство x £ x). Если высказываемое утверждение не имеет места, то, следовательно, неравенство x £ x выполняется не для каждого xÎA, значит существует элемент xÎA, для которого неравенство x £ x не выполняется.
Пример 2. Используя закон Моргана, построить отрицание предела функции f(x) в точке x=а. Сформулируем определение предела функции f(x) в точке x=a по Коши с использованием введенной символики:
Здесь на языке алгебры записано: вещественное число b называется пределом функции f(x) в точке x=a, если для любого вещественного положительного числа ε найдется вещественное положительное число d, что для всех значений аргумента x из области определения таких, что, если выполнены неравенства
Операции над множествами Объединение АÈВ множеств А и В Множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из данных множеств, называется объединением множеств А и В. Указанное определение легко распространяется на случай трех и более множеств:
Пример 1. А{1,2,3,4,5}, В{1,2}, АÈВ={1,2,3,4,5}. Множество АÈВ по определению не содержит неразличимых элементов и, следовательно, элементы 1 и 2, входящие в множества А и В, входят в АÈВ один раз. Пересечение АÇВ множеств А и В есть множество элементов, принадлежащих и А и В.
Пример 2. А{1,2,3,4,5}; В{1,2} АÇВ={1,2} Два множества А и В называются непересекающимися, если АÇВ=Ø.
Разность А\В множеств А и В Разностью множеств А и В называется совокупность тех элементов А, которые не содержатся в В.
Пример 3. А={1,2,3,4,5}, В={1,2} А\В={3,4,5}.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. , или xÏA, означает, что x не есть элемент множества А.
, или xÏA, означает, что x не есть элемент множества А.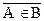 . Знаки Î, Ì, Í, É, Ê называются знаками включения.
. Знаки Î, Ì, Í, É, Ê называются знаками включения. – для любого xÎA выполняется предложение a.
– для любого xÎA выполняется предложение a.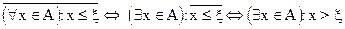
 .
. , будет следовать неравенство
, будет следовать неравенство 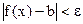 .
.