|
|
А условие прочности на смятие
FtAсм σсм ,
где Ft – срезающая сила (осевая или окружная); i – число поверхностей среза;
– площадь штифта при срезе;
– площадь поверхности смятия (сжатия); = 70–80 МПа – допускаемое напряжение при срезе; = 200–300 МПа – допускаемое напряжение при смятии.
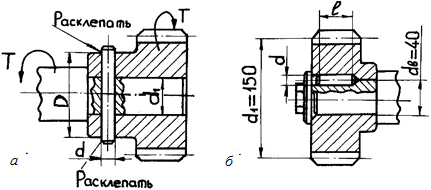
Рис. 26.15. Схемы к расчету соединений радиальным (а) и осевым (б) штифтами: d – диаметр штифта; d1 – диаметр вала
Осевые штифты (круглые шпонки) применяют в машинострое- нии для передачи вращающего момента в неразъемных соединениях. Штифты диаметром d = (0,1–0,15)dви длиной l = (3–4)dв (dв – диаметр вала) устанавливают по посадке с натягом Н7/r6 в отверстия, сов- местно просверленные и развернутые при сборке в валу и ступице по
Число штифтов для передачи заданного вращающего момента
Многоштифтовые соединения этого типа по прочности близки к шлицевым.
Резьбовые соединения Резьбовыми называют соединения деталей с помощью резьбы. Они являются наиболее распространенным видом разъемных соеди- нений.
26.5.1. Крепежные детали и стопорящие устройства Наибольшее распространение среди резьбовых деталей полу- чили крепежные болты, винты, шпильки, гайки. Под болтом или винтом понимают стержень с головкой и одним резьбовым кон- цом. Шпилька имеет два резьбовых конца. Гайка – это деталь с резьбовым отверстием. С помощью этих деталей образуют разъемные соединения бол- том, винтом и шпилькой в разнообразных конструкциях. Тип со- единения определяется прочностью материалов соединяемых дета- лей, частотой сборки и разборки соединений в эксплуатации, а так- же особенностями конструкции и технологии изготовления со- единяемых деталей. Для предохранения повреждений поверхностей соединяемых де- талей при завинчивании и увеличения опорной поверхности гайки используют шайбы. При статических нагрузках самоотвинчивания резьбовых дета- лей не наблюдается, так как все крепежные резьбы выполняются самотормозящимися (явление самоотвинчивания не должно наблю- даться). При динамических и вибрационных нагрузках может про- изойти самоотвинчивание гаек и винтов.
Штифты, винты, упругие контргайки, проволока также могут выполнять функции стопорения. Болты, винты, шпильки и гайки изготавливают из мало- и сред- неуглеродистых сталей Ст 3 кп, Ст 5, 10, 10 кп, 15, 20, 30, 45 и др. В ответственных случаях (ударные нагрузки, высокие температуры) применяют легированные стали 40Х, 38ХА, 30ХГСА, 35ХГСА, 40ХН2МА и др., а также титановые сплавы (резьбовые детали из титановых сплавов по сравнению со стальными имеют повышен- ную прочность и примерно в два раза легче). Пружинные шайбы изготавливают из рессорно-пружинных ста- лей 65, 70, 75, 65Г. Гайки изготавливают из стали Ст 3. Механические характеристики материалов крепежных деталей нормированы ГОСТ 1759–82. Для стальных болтов, винтов и шпи- лек предусмотрено 12, а для гаек – семь классов прочности и соот- ветствующие им марки сталей.
26.5.2. Резьба и ее параметры Резьба является основным элементом резьбового соединения. Она образует выступы по винтовой линии на поверхности винта и гайки (наружная и внутренняя), может изготавливаться на ци- линдрической (цилиндрическая резьба) и конической (кониче- ская резьба) поверхностях заготовки, бывает правая, если винто- вая линия направлена вверх слева направо, и левая – при направ- лении ее вверх права налево. Наиболее применяемые правые резьбы. Если на поверхность детали наносится один винтовой выступ, резьбу называют однозаходной. Применяют также мно- гозаходные резьбы. Основные параметры цилиндрической резьбы (рис. 26.16): d, D – наружные диаметры соответственно болта и гайки; d1, D1; d2, D2 – внутренние и средние диаметры резьбы; d3 – внутренний диаметр болта по дну впадины; Р – шаг (расстояние между одноименными сторонами двух смежных профилей); ψ – угол подъема резьбы, т. е. угол развертки винтовой линии по среднему диаметру резьбы: tgψ ;
По форме профиля крепежные резьбы бывают треугольные и круглые; резьбы винтовых механизмов (ходовые резьбы) – трапеце- идальные, упорные, прямоугольные. Метрическая резьба (ГОСТ 24705–81) – основной вид резьбы крепежных деталей (см. рис. 26.16). Она бывает с крупным и мел- ким шагом, но чаще выполняют наиболее износостойкую и техно- логичную резьбу с крупным шагом. Дюймовая резьба подобна метрической (α = 55°, у метрической α = 60°). Трубные резьбы (цилиндрическая и коническая) служат для со- единения труб и арматуры. Трапецеидальная резьба технологична, отличается высокой прочностью витков и является основной для винтовых механизмов. Упорная резьба имеет несимметричный профиль витков и вы- полняется на винтах, воспринимающих значительную односторон- нюю нагрузку. Прямоугольная резьба сложна в изготовлении и применяется редко.
Резьбу получают методом резания, накатыванием, литьем и прессованием.
26.5.3. Силовые зависимости в резьбовом соединении Надежность резьбового соединения оценивается легкостью сборки (легкостью затяжки гайки или болта) и сохранностью затяж- ки (самоторможением). При завинчивании гайки надо преодолеть момент сопротивления затяжки Т3 = Tр + Tт,
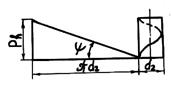
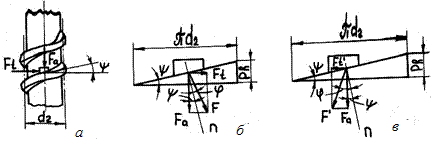
где Tр – момент сил трения в резьбе; Тт – момент сил трения на опорном торце гайки. Для определения Тр и Тт необходимо установить зависимость между силами, возникающими в винтовой паре при завинчивании. Развернем среднюю винтовую линию резьбы на плоскость, а гайку представим в виде ползуна (рис. 26.18, а).
Рис. 26.18. К анализу сил в винтовой паре
При подъеме ползуна по наклонной плоскости (это соответст- вует завинчиванию гайки) сила F взаимодействия наклонной плос- кости с движущимся ползуном представляет собой равнодейству- ющую нормальной силы и силы трения. Из схемы сил, действую- щих на ползун (рис. 26.18, б),
где φ Ft ,
f – коэффициент трения. При перемещении ползуна вниз (рис. 26.18, в)
где Ft – окружная сила при отвинчивании гайки.
(26.5)
Силу трения на торце гайки f1·F, зависящую от коэффициента трения f1 на торце гайки, считают сосредоточенной и приложенной к среднему радиусу опорной поверхности (рис. 26.19, а):
Dср
(26.6) Момент сопротивления затяжки Tз преодолевается моментом си- лы, приложенной к гаечному ключу (рис. 26.19, б). Приравняв оба момента, получим
Fкл
Рис. 26.19. К определению момента завинчивания
ских резьб можно принять: ψ = 2,5°; d2 0,9d ; Dср ;
Fa . Таким образом, сила в 1 H, приложенная на конце ключа, создает силу прижатия деталей 60–100 Н. Такой вы- игрыш в силе обеспечивает легкость сборки соединения. 26.5.4. Самоторможение и коэффициент полезного действия винтовой пары
рис. 26.18, в) Ft 0 или tg φ , то резьба будет самотормо- зящейся. Условие самоторможения:
ψ < φ.
фициента трения в пределах от 6° (при f ) до 11° (при
свойство проявляется главным образом при статических нагрузках. При переменных нагрузках условие самоторможения не соблюдает- ся. Поэтому необходимо стопорение резьбовых соединений. Коэффициент полезного действия винтовой пары определяют
как отношение , где Tз
находят по формуле (26.6), а
ψ ; т. к. большинство винтовых механизмов самотор- мозящиеся, их КПД меньше 0,5. 26.5.5. Расчет резьбовых соединений на прочность Виды разрушения резьбовых крепежных деталей: разрыв стерж- ня по резьбе или переходному сечению у головки; повреждение или разрушение резьбы (смятие и износ, срез, изгиб); повреждение го- ловки болта (винта). Размеры стандартных болтов, винтов и шпилек отвечают усло- вию равнопрочности всех элементов соединения. Поэтому можно ограничиваться расчетом по одному, основному критерию – проч- ности нарезной части, а размеры винтов, болтов и гаек принимать по таблицам стандарта в зависимости от рассчитанного диаметра резьбы. Длину болта, винта и шпильки выбирают в зависимости от толщины соединяемых деталей. Рассмотрим расчет на прочность резьбовых соединений при по- стоянной нагрузке. Болт нагружен внешней силой F (болт без предварительной за- тяжки), например, нарезанный участок крюка для подвешивания груза. Опасным является сечение крюка, ослабленное нарезкой (рис. 26.20). Из условия прочности на растяжение
откуда
где = 0,6 – допускаемое напряжение при рас-
Рис. 26.20. Крюковая подвеска
Болт затянут силой затяжки Fз, а внешняя нагрузка отсутствует (ненагруженные крышки, кронштейны и т. п.). Стержень болта ис- пытывает совместное действие растяжения и кручения, т. е. растя- гивается осевой силой Fз от затяжки болта и скручивается момен- том, равным моменту сил трения в резьбе Tp(формула (26.5)), Прочность таких болтов (рис. 26.21) определяют по эквивалентному напряжению
где σp σэ
τк – напряжение от кручения:
к
S – требуемый коэффициент запаса прочности болта, прини- маемый в зависимости от материала болта, характера нагрузки и диаметра болта.
Для стандартных метрических резьб σэ , т. е. расчет бол-
Расчетный диаметр резьбы болта определяют по формуле (26.9), принимая F = Fр. Болтовое соединение нагружено силами, сдвигающими детали в стыке. Условием надежности соединения является отсутствие сдви- га деталей в стыке. В соединении с зазором (рис. 26.22, а) болт устанавливают с предварительной затяжкой. Внешняя сила F непосредственно на болт не передается, поэтому его рассчитывают на растяжение по силе затяжки Fз.
Рис. 26.22. К расчету болта, нагруженного поперечной силой: а – поставленного с зазором; б – без зазора Во избежание сдвига деталей при наличии зазора сила трения на поверхностях стыка должна быть не меньше внешней сдвигающей силы F:
где i – число стыков в соединении; f – коэффициент трения; K – коэффициент запаса (K = 1,3–1,5 при статической и K = = 1,8–2,0 при переменной нагрузке); z – число болтов в соединении. Болт в этом случае рассчитывают по силе затяжки:
При установке болта без зазора (рис. 26.22, б) предварительная затяжка не требуется. Болт испытывает срез и смятие. Стержень болта рассчитывают на срез, а при тонких деталях – и на смятие. Условия прочности
где τ, τ – соответственно расчетное и допускаемое напряжения для материала болта на срез, τ = (0,2–0,3) σт; do – диаметр ненарезанной части болта; σсм , σсм – соответственно расчетное и наименьшее допуска-
S – наименьшая толщина детали. σсм = Болт затянут, а внешняя нагрузка стремится раскрыть стык (бол- ты для крепления крышек резервуаров для газа и жидкости, на- груженные давлением выше атмосферного, крепления цилиндров, насосов, станин к фундаментам и др.). Затяжка болтов должна обес- печить герметичность соединения или нераскрытие стыка (не допу- стить появления зазора) под нагрузкой. Эта задача решается с уче- том деформации деталей соединения. Внешняя нагрузка F (R – равнодействующая нагрузки; z –
число болтов) вызывает удлинение болта на Δδ (рис. 26.23), а де- формация деталей уменьшается на ту же величину. Нагрузка со стороны деталей на болт также уменьшится. Именно поэтому счи-
а б Рис. 26.23. К расчету затянутого болта с учетом деформации и соединенных деталей
Суммарная нагрузка на затянутый болт
(26.10)
где χ – коэффициент внешней нагрузки, показывающий, какая часть внешней нагрузки воспринимается болтом (учитывает подат- ливость болта и соединяемых деталей). Величина χ – определяется по условию равенства дополнитель- ных деформаций болта и деталей:
где λб , λд – коэффициенты податливости соответственно болта и
Из равенства (26.11) следует, что
Точный расчет коэффициента χ сложен, а так как на практике величину затяжки болтов в большинстве случаев не контролируют, то смысл точного расчета теряется. При приближенных расчетах принимают: – для соединений стальных и чугунных деталей без упругих про- кладок χ = 0,2–0,3; – для соединения тех же деталей, но с упругими прокладками (резина, полиэтилен, асбест, паронит и др.) χ = 0,4–0,5. Предварительная затяжка болта Fз должна быть больше мини- мальной силы предварительной затяжки болта:
Из условия сохранения плотности стыка соединяемых деталей (невозможности образования зазора) принимают
где Kз – коэффициент запаса предварительной затяжки: при посто- янной нагрузке Kз = 1,25–2,0; при переменной Kз = 2,5–4.
26.5.6. Расчет резьбовых соединений при переменном режиме нагружения Крепежные детали, работающие при переменном режиме нагру- жения, рассчитывают на усталость. Болты устанавливаются с пред- варительной затяжкой, при которой создается напряжение
четной силы Fб значительно меньше по сравнению с изменением внешней силы F. Расчет на усталость ведут как проверочный по двум коэффициен- там запаса прочности: по амплитуде цикла и по наибольшему напря- жению цикла (рис. 26.24). Предварительно болт рассчитывают из условия его статической прочности с учетом формул (26.10) или (26.12).
Рис. 26.24. Циклы переменных напряжений
Коэффициент запаса прочности по амплитуде цикла
a
σa – амплитуда переменных напряжений:
a Sa – требуемый коэффициент запаса прочности по амплитуде Sa = 2,5–4,0. Коэффициент запаса по наибольшему напряжению цикла
где Sa = 1,25–2,5. При Sa ≥ Sa и S ≥ [S] болт удовлетворяет условию проч-
За счет уменьшения коэффициента внешней нагрузки может быть повышена прочность резьбового соединения при переменных нагрузках. Это может быть достигнуто уменьшением податливости стыка и увеличением податливости болта, в частности, диаметр стержня болта уменьшают до диаметра d3.
ЛИТЕРАТУРА 1. Аркуша, А.И. Руководство к решению задач по теоретиче- ской механике / А.И. Аркуша. – М.: Высш. школа, 1989; 1990; 1999. 2. Артоболевский, И.И. Теория механизмов и машин / И.И. Артоболевский. – М.: Машиностроение, 1975. – 639 с. 3. Артоболевский, И.И. Сборник задач по теории механизмов и машин / И.И. Артоболевский, Б.В. Эдельштейн. – М.: Маши- ностроение, 1975. – 256 с. 4. Беляев, Н.М. Сопротивление материалов / Н.М. Беляев. – М.: Наука, 1976. – 608 с. 5. 6. Дубейковский, Е.Н. Сопротивление материалов: учебное по- собие для машиностроительных специальностей технику- мов / Е.Н. Дубейковский, Е.С. Савушкин. – М.: Высшая шко- ла, 1985. –192 с. 7. Иосилевич, Г.Б. Прикладная механика: учеб. для вузов / Г.Б. Иосилевич, Г.Б. Строганов, Г.С. Маслов; под ред. Г.Б. Иоси- левича. – М.: Высшая школа, 1989. – 360 с. 8. Ицкович, Г.М. Сборник задач по сопротивлению материалов: учебное пособие / Г.М. Ицкович, А.И. Винокуров, Н.В. Ба- рановский. – 4-е изд. – Л.: Судостроение, 1972. 9. Каленик, В.В. Текст лекций по разделу «Теория механизмов и машин» курса «Прикладная механика» для студентов немеха- нических специальностей / В.В. Каленик, В.К. Акулич. – Минск: БПИ, 1983. 10. Кильчевский, Н.А. Основы теоретической механики / Н.А. Киль- чевский, Н.И. Ремизова, Н.Н. Шепелевская. – Киев: Технiка, 1968. – 260 с. 11. Кинасошвили, Р.С. Сопротивление материалов / Р.С. Кина- сошвили. – М.: Главная редакция физико-математической литературы изд-ва «Наука», 1975. – 384 с. 12. Методические указания по решению задач по курсу «При- кладная механика» для студентов немеханических специаль- ностей: в 2 ч. / А.А. Миклашевич [и др.]. – Минск: БПИ, 1985. – Ч 2. – 37 с. 13. Мовкин, М.С. Теоретическая механика / М.С. Мовкин, А.Б. Из- раелит. – Л.: Судостроение, 1972. 14. Никитин, Е.М. Теоретическая механика для техникумов / Е.М. Никитин. – М.: Наука, 1971 (и последующие издания). 15. Осадчий, В. И. Руководство к решению задач по теоретиче- ской механике / В.И. Осадчий, А.М. Фаин. – М.: Высш. шко- ла, 1972. 16. Павловский, М.А. Теоретическая механика: в 2 ч. / М.А. Пав- ловский, Л.Ю. Акинфеева, О.Ф. Бойчук. – Киев: Вища шко- ла, 1989; 1990. – 350 с. 17. Подскребко, М.Д. Задания по расчетно-графическим работам курса «Прикладная механика»: в 2 ч. / М.Д. Подскребко,
18. Пособие к решению задач по сопротивлению материалов: учеб. пособие для техн. вузов / И.М. Миролюбов [и др.]. – 5-е изд., перераб. и доп. – М.: Высшая школа, 1985. – 399 с. 19. Прикладная механика: методические указания и контрольные задания для студентов-заочников / под ред. П.Г. Гузенкова. – М.: Машиностроение, 1982. – 112 с. 20. Прикладная механика: учеб. пособие/ А.Т. Скойбеда [и др.]; под общ. ред. А.Т. Скойбеды. – Минск: Вышэйшая школа, 1997. – 552 с. 21. Руденок, Е.Н. Техническая механика: сб. заданий: учеб. по- собие / Е.Н. Руденок, В.П. Соколовская. – Минск: Высшая школа, 1990. – 238 с. 22. Сборник задач по сопротивлению материалов / под ред. В.К. Качурина. – М.: Наука, 1970. – 432 с. 23. Сборник задач по технической механике / В.В. Багреёв [и др.]. – Л.: Судостроение, 1968. 24. Соколов, Б.Ф. Методические указания к семестровым задани- ям по объединенному курсу «Теоретическая и прикладная ме- ханика» / Б.Ф. Соколов [и др.]. – Челябинск: Челябинский ин-т механизации и электрификации сельского хозяйства, 1985. 25. Феодосьев, В.И. Сопротивление материалов / В.И. Фе- одосьев. – М.: Наука, 1986. – 512 с. 26. Феодосьев, В. И. Избранные задачи и вопросы по сопротив- лению материалов / В.И. Феодосьев. – 4-е изд., испр. и доп. – М.: Главная редакция физико-математической литературы изд-ва «Наука», 1973. – 400 с. 27. Шапиро, Д.М. Сборник задач по сопротивлению материалов: учебное пособие для машиностроительных техникумов / Д.М. Шапиро, А.И. Подорванова, А.Н. Миронов. – 3-е изд., перераб. – М.: Высшая школа, 1970. 28. Юдин, В.А. Теория механизмов и машин / В.А. Юдин, Л.В. Петрокас. – М.: Машиностроение, 1977. – 527 с. 29. Яблонский, А.А. Курс теоретической механики: в 2 ч. / А.А. Яблонский. – 7-е изд., стереотип. – СПб.: Лань, 1999. – Ч. 1: Статика, кинематика.
П1. Сталь горячекатаная. Балки двутавровые. ГОСТ 8239–89.
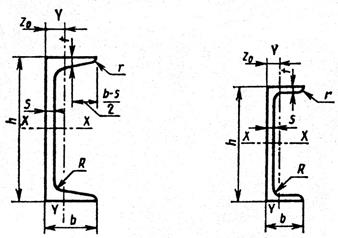
h – высота двутавра; b – ширина полки; s – толщина стенки; t – средняя толщина полки; R – радиус внутреннего скругления; r – радиус скругления полки.
П2. Сталь горячекатаная. Швеллер. ГОСТ 8240–89
h – высота; b – ширина полки; s – толщина стенки; t – толщина полки; Обозначения:
r – радиус скругления полки; Z0 – расстояние от оси Y–Y до наружной грани стенки.

Швеллеры с уклоном внутренних граней полок
Швеллеры с параллельными гранями полок

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
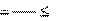 σсм
σсм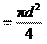 Ac
Ac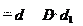 Ac τc σсм
Ac τc σсм
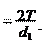 Срезающая сила при передаче вращающего момента Ft
Срезающая сила при передаче вращающего момента Ft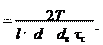 z
z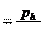 πd2
πd2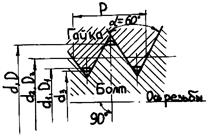
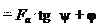
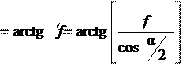 – приведенный угол трения;
– приведенный угол трения;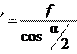 f – приведенный коэффициент трения в резьбе;
f – приведенный коэффициент трения в резьбе;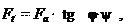
 Полагая, что сила Ftсосредоточена и приложена к среднему ра- диусу резьбы 0,5d2 (см. рис. 26.19, а):
Полагая, что сила Ftсосредоточена и приложена к среднему ра- диусу резьбы 0,5d2 (см. рис. 26.19, а):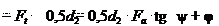 Tp .
Tp .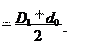
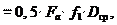 Tт
Tт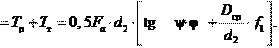 Tз
Tз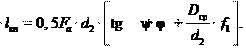 (26.7)
(26.7)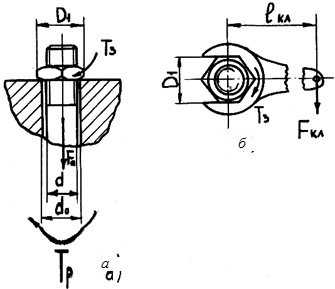

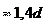 Величины, входящие в формулу (26.7), имеют определенные значения. Например, при стандартном ключе lкл 15d для метриче-
Величины, входящие в формулу (26.7), имеют определенные значения. Например, при стандартном ключе lкл 15d для метриче-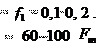
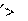
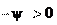 Если при опускании ползуна по наклонной плоскости (см.
Если при опускании ползуна по наклонной плоскости (см.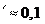 Для крепежных резьб угол подъема резьбы ψ = 2°30'–3°30', а приведенный угол трения φ изменяется в зависимости от коэф-
Для крепежных резьб угол подъема резьбы ψ = 2°30'–3°30', а приведенный угол трения φ изменяется в зависимости от коэф-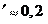 f ). Таким образом, все крепежные резьбы – самотормозящи- еся. Это объясняет важное преимущество крепежной резьбы – надежное стопорение гайки (винта) в любом положении. Однако это
f ). Таким образом, все крепежные резьбы – самотормозящи- еся. Это объясняет важное преимущество крепежной резьбы – надежное стопорение гайки (винта) в любом положении. Однако это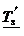 Tз
Tз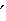 – по той
– по той η= tgψ . tg ψ + φ
η= tgψ . tg ψ + φ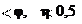 С увеличением ψ и уменьшением φ коэффициент полезного действия возрастает. Для самотормозящейся винтовой пары, где
С увеличением ψ и уменьшением φ коэффициент полезного действия возрастает. Для самотормозящейся винтовой пары, где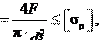 σp (26.8)
σp (26.8)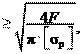 d3 (26.9)
d3 (26.9)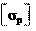
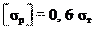

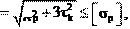 – напряжение от растяжения, определяемое по форму-
– напряжение от растяжения, определяемое по форму-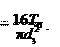 τ
τ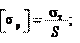
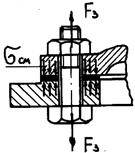
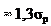 Рис. 26.21. К расчету болта, нагруженного только силой затяжки
Рис. 26.21. К расчету болта, нагруженного только силой затяжки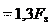 Fр .
Fр .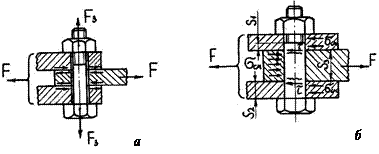
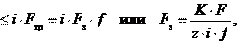 F
F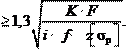 dз
dз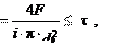 τ
τ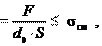 σсм
σсм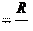 z
z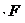 тают, что болт воспринимает часть внешней нагрузки χ .
тают, что болт воспринимает часть внешней нагрузки χ .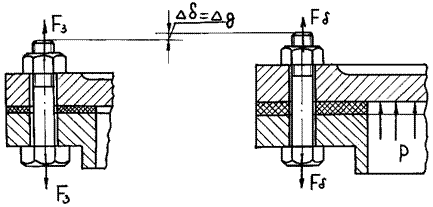
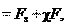 Fδ
Fδ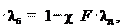 χF (26.11)
χF (26.11) χ = λд . λб + λд
χ = λд . λб + λд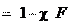 Fз min .
Fз min .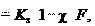 Fз
Fз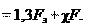 Fh (26.12)
Fh (26.12)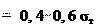 σз . Вследствие этого циклическое изменение рас-
σз . Вследствие этого циклическое изменение рас-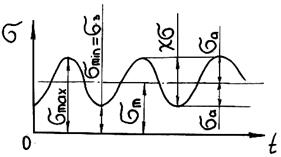
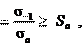 S
S где σ 1 – предел выносливости материала болта (шпильки);
где σ 1 – предел выносливости материала болта (шпильки);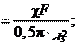 σ
σ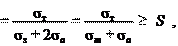 S
S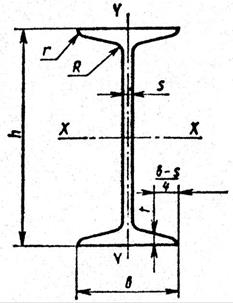 Обозначения:
Обозначения: