
|
|
Фасонное зубофрезерование зубчатых колес
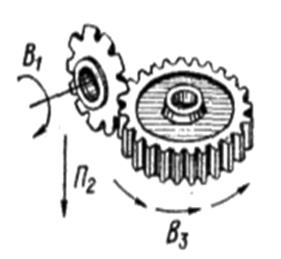
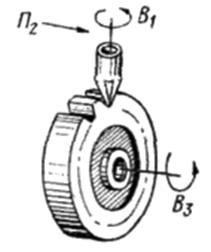
На рис. 3.52 представлены схемы способов фасонного зубофрезерования. При фрезеровании впадин фрезе сообщают движение скорости резания Фv(В1) и движение подачи Фs(П2). Обратный отвод фрезы в исходное положение производят на ускоренном ходу. Затем движением деления Д(В3) заготовку поворачивают на угловой шаг зубьев. Дисковые модульные фрезы используют для нарезания цилиндрических и прямозубых конических колес, а пальцевые – для нарезания цилиндрических и шевронных колес. Основное достоинство рассматриваемых схем - простота кинематики станков из-за отсутствия в их структуре сложных групп формообразования профиля зубьев.
а б Рис. 3.52. Формообразование зубьев цилиндрических колес модульными фрезами: а – фасонной дисковой; б – фасонной пальцевой
Недостаток – потребность в большом количестве фрез одинакового модуля из-за изменения профиля впадины для разного числа зубьев нарезаемых колес. Частично этот недостаток компенсируется посредством использования различных комплектов фрез. Для каждого модуля эти комплекты насчитывают 8, 15 и 26 фрез. Фасонное зубофрезерование модульными фрезами является неточным и мало призводительным. Погрешность профиля фрезы полностью копируется деталью. Угловой шаг и форма впадины между зубьями зависят от диаметра колеса и точности делительных устройств. Низкая производительность вызывается прерывистым характером обработки. Поэтому рассматриваемые схемы используют в еденичном и ремонтном производствах. Процесс зубонарезания осуществляют на горизонтальных или вертикальных фрезерных станках с использованием делительных головок. Делительная головка, установленная на фрезерном станке, выполняет функцию группы деления. Делительные головки бывают простые и универсальные, лимбовые и безлимбовые. В простых делительных головках шпиндель расположен горизонтально, в универсальных – шпиндель помещен в поворотный корпус и может располагаться под углом.
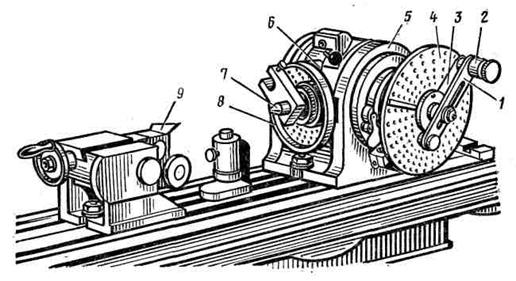
Универсальная делительная головка (УДГ) выполнена в виде шпиндельной бабки (рис. 3.53), несущей поворотный корпус 5, в котором смонтирован шпиндель 7, кинематически связанный с рукояткой 1 и лимбом 4. Лимб имеет несколько рядов отверстий, равномерно расположенных на концентрических окружностях. Для удобства отсчета используется раздвижной сектор 3. Рукоятка 1, поворачиваемая при делении относительно лимба, оснащена фиксатором 2, который можно вставлять в любое отверстие лимба. В комплект головки входит также задняя бабка 9 и гитара сменных зубчатых колес, используемая при дифференциальном делении, нарезании косозубых колес и винтовых канавок. В ряде конструкций для непосредственного деления используют диск 8 и фиксатор 6. Рис. 3.53. Универсальная лимбовая делительная головка
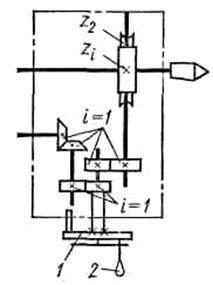
Основным техническим параметром УДГ является характеристика, определяемая числом оборотов N рукоятки управления, необходимым для одного полного оборота ее шпинделя. Обычно характеристика УДГ, в зависимости от конструкции, равна передаточному числу делительной червячной передачи: 40, 60, 80 или 120. Лимб УДГ имеет различное число отверстий а на делительных окружностях с обеих сторон: первая сторона – 24, 25, 28, 30, 34, 37, 38, 39, 41, 42, 43; вторая сторона – 46, 47, 49, 51, 53, 54, 57, 58, 59, 62, 66. В гитару входит комплект сменных зубчатых колес с числами зубьев: 25 (2), 30, 35, 40, 50, 55, 60, 70, 80, 90, 100. Деталь устанавливают в центрах шпиндельной и задней бабок или в трехкулачковом патроне, навертываемом на резьбовой конец шпинделя. Простое деление (рис. 3. 54,а) используется тогда, когда можно подобрать на лимбе окружность с нужным числом отверстий. Это деление осуществляют при зафиксированном лимбе 1 и снятой гитаре iд. Простое деление осуществляют поворотом рукоятки 2 на б отверстий относительно лимба, на окружности которого расположено, а отверстий, т.е. рукоятку поворачивают на угол б/а. Если б < а, поворот рукоятки составляет меньше 360о; если б = а, то 360о (один оборот); если б > а, то больше 360о. Для расчетной цепи деления, совпадающей с внешней связью кинематической группы деления, РП имеют вид п оборотов рукоятки → 1/z поворота шпинделя, УКЦ: где z – число частей, на которое требуется выполнить деление. Следовательно, ФН: n = N/z.
Выделим из ФН целое число оборотов А. Тогда,
 . .
а б
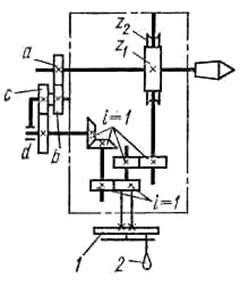
Рис.3. 54. Схемы настройки лимбовой УДГ
В полученном выражении m подбирают таким, чтобы am соответствовало числу отверстий на одной из окружностей лимба. Тогда, при делении рукоятку УДГ поворачивают на А (целое число) раз и дополнительно на часть оборота, соответствующую бm отверстий на окружности аm лимба. При отсчете числа б отверстий на лимбе используют раздвижной сектор (см. рис. 3. 53), состоящий из двух радиальных раздвижных линеек. Дифференциальное деление (рис. 3.54,б) применяют тогда, когда не удается разделить число зубьев заготовки простым делением. В этом случае необходимо лимб головки расфиксировать и подобрать, кроме угла поворота рукоятки б/а, еще и сменные зубчатые колеса для гитары iд=a/b∙c/d Тогда при повороте рукоятки относительно лимба на угол б/а через гитару iд и конические колеса с передаточным отношением i = 1 лимб при делении будет поворачиваться, а вместе с ним и фиксирующее гнездо, в которое необходимо вставить фиксатор рукоятки. При расчете настройки задают zф, близкое к z, для которого можно подобрать на лимбе окружность с требуемым количеством отверстий. Пользуясь ФН для простого деления, определяют
по которому устанавливают угол поворота рукоятки. В итоге при каждом делении возникает ошибка ∆ = ± (N/z – N/zф) = ± N (zф - z) / zф ∙ z, которую необходимо компенсировать дополнительным поворотом лимба в зависимости от знака ошибки. Компенсация обеспечивается соответствующим подбором сменных зубчатых колес для гитары iд. РП для расчетной цепи, соединяющей шпиндель с лимбом 1, имеют вид 1/z об. шпинделя → N (zф – z) / zф ∙z дополнительного поворота лимба. УКЦ:
ФН:
Пример. Настроить УДГ (N = 40) для нарезания на заготовке 67 зубьев. Примем zф = 60. По ФН для простого деления По полученному значению раздвигаем радиальные линейки раздвижного сектора на 40 отверстий на окружности лимба, состоящей из 60 отверстий. По ФН для гитары сменных зубчатых колес
Знак минус показывает, что при делении лимб должен вращаться в противоположном направлении к вращению рукоятки. В этом случае в гитару настройки необходимо ввести промежуточную шестерню, например, z = 25. По полученному значению из имеющегося набора устанавливаем сменные зубчатые колеса
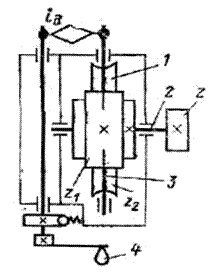
Рассмотренная УДГ, по существу, - это дифференциал, осуществляющий при дифференциальном делении алгебраическое сложение двух движений на одном исполнительном звене – шпинделе. Первый вход дифференциала – рукоятка, второй вход – лимб. При этом движение на второй вход сообщается от общего исполнительного звена – шпинделя. Такой дифферен Рис.3.55. Безлимбовая УДГ циал называют замкнутым. Простая безлимбовая делительная головка (рис. 3.55) состоит из делительной червячной передачи, червячное колесо 1 которой установлено на шпинделе 2 головки, а вал червяка 3 через гитару сменных зубчатых колес соединен с рукояткой 4, которую при делении поворачивают на один оборот. Настройку головки для деления на разное число z осуществляют подбором сменных зубчатых колес гитары. РП для вывода ФН: 1 об. рукоятки 4 → 1/z поворота шпинделя. УКЦ: 1/z = 1∙ iд ∙ z1/z2, где z1 - число заходов червяка, равное, как правило, 1; z2 - число зубьев червячного колеса (характеристика головки). ФН: iд = z2/z = N/z. Возможности простой безлимбовой головки ограничены простым делением. Известны также безлимбовые УДГ, отличающиеся от лимбовой (см. рис. 3.54) тем, что в них вместо лимба установлена гитара деления и планетарный дифференциал. Гитара деления связывает рукоятку с водилом (первый вход дифференциала), а шпиндель головки соединен посредством гитары, используемой при дифференциальном делении, с центральным колесом (второй вход дифференциала). Методика вывода ФН для безлимбовой УДГ аналогична рассмотренной выше для лимбовой головки. Лимбовые и безлимбовые УДГ используют также при фрезеровании винтовых канавок на сверлах, зенкерах, фрезах и нарезании косозубых колес. На рис. 3.56 приведена схема фрезерования стружечных канавок на универсальных фрезерных станках с применением лимбовой УДГ. Заготовка 4 закреплена в шпинделе делительной головки 1, установленной на столе 3 горизонтально – фрезерного станка. Стол развернут на угол αподьема винтовой линии стружечной канавки. Вал 2 делительной головки через гитару iд сменных зубчатых колес соединен с ходовым винтом продольной подачи стола. При фрезеровании столу сообщается продольная подача относительно вращающейся фрезы 5, при этом от ходового винта вращение передается через гитару iд шпинделю с заготовкой. Угол α определяют из выражения
где D - диаметр заготовки; tк. – шаг винтовой канавки. За один оборот заготовки стол должен переместиться на шаг винтовой канавки. Следовательно, УКЦ можно записать в виде
где tТВ – шаг ходового винта станка. ФН: iд = 40 tтв / tк.
Деление для фрезерования следующей канавки осуществляется поворотом рукоятки головки. Методика определения угла поворота рукоятки и его установка приведены при описании лимбовой УДГ. Рис.3.56. Схема фрезерование стружечных канавок
Приведенная ФН для фрезерования винтовых канавок используется также при нарезании косозубых колес. В этом случае шаг винтовой канавки определяют из выражения
где z – число зубьев нарезаемого колеса; m – модуль. На фрезерных станках с применением УДГ можно фрезеровать плоские кулачки, у которых рабочий профиль выполняется по архимедовой спирали. В этом случае при использовании горизонтально – фрезерного станка шпиндель головки устанавливается вертикально. ФН для гитары iд имеет вид: iд = 40 tтв / h, где h – шаг архимедовой спирали, равный разности большего и меньшего радиусов рабочего профиля кулачка. Если для заданного шага архимедовой спирали невозможно подобрать сменные зубчатые колеса, задают hф, а шпиндель поворачивают на угол γ от вертильного положения. Его значение определяют из выражения γ = arc cos h/hф. При использовании УДГ для обработки винтовых профильных поверхностей головка выполняет на универсальных фрезерных станках две функции: группы деления Д (В) и исполнительного звена винторезной группы Фs (В П), получаемой из группы продольной подачи Фs(П) фрезерного станка. Внутренняя связь этой группы – кинематическая цепь, связывающая стол фрезерного станка со шпинделем делительной головки. Винтовое движение воспроизводимое этой группой имеет незамкнутую траекторию, и настраивается по пяти параметрам: на траекторию – гитарой iд, на скорость – коробкой подач фрезерного станка, на направление – реверсом, установленном на ходовом винте станка, на путь и исходную точку – по упорам. В крупносерийном производстве фасонное зубофрезерование используют для черновой прорезки впадин прямозубых цилиндрических и конических колес на многошпиндельных полуавтоматах, например, ЕЗ-5 и ЕЗ-40. Этот вид обработки используется так же в инструментальном производстве для прорезки винтовых канавок при обработке сверл, зенкеров, метчиков. Для этого используют специальные фрезерные станки, полуавтоматы и автоматы. Например, полуавтомат для фрезерования сверл модели 679У.
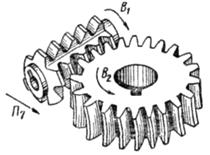
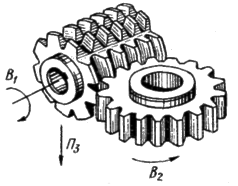
Зубофрезерные станки На зубофрезерных станках червячными фрезами нарезают цилиндрические колеса с прямыми и винтовыми зубьями внешнего зацепления и червячные колеса. На рис. 3.57 приведены схемы взаимодействия червячной фрезы и нарезаемого колеса. При зубофрезеровании профилирование цилиндрических колес с прямыми и винтовыми зубьями и червячных колес осуществляется движением обката Фv (В1В2), состоящим из двух элементарных согласованных вращательных движений: В1- вращения фрезы и В2- вращения заготовки, воспроизводящих червячное зацепление. При таком методе профилирования зубьев колес нет необходимости в отдельной группе деления. Линия зуба по длине воспроизводится методом касания, но для каждой из рассматриваемых схем по-разному. При нарезании цилиндрического прямозубого колеса (рис. 3.57,а) вместе с движением В1 скорости резания фрезе сообщается также формообразующее движение подачи Фs (П3). Таким образом, функционально несвязанные между собой движения фрезы В1 и П3 методом касания воспроизводят прямую линию зуба цилиндрического колеса. Следовательно, формообразующая часть кинематической структуры зубофрезерного станка для нарезания прямозубых колес должна содержать две группы – сложную Фv(В1 В2) и простую Фs (П3). У цилиндрического колеса с винтовыми зубьями линия зуба имеет винтовую форму. Ее воспроизведение осуществляется сложным формообразующим движением Фs(П3В4), состоящим из двух согласованных элементарных движений: П3 фрезы и В4 заготовки нарезаемого колеса. Следовательно, формообразующая часть кинематической структуры станка для нарезания колес с винтовым зубом должна содержать две сложных группы – Фv (В1В2) и Фs (П3В4). При формообразовании червячных колес используют две основные схемы: классическую пионерную с радиальным врезанием фрезы и производную с касательным (тангециальным) врезанием. При нарезании червячных колес с радиальным врезанием (рис. 3.57,б) одновременно с движением обката фрезе дополнительно сообщают элементарное движение радиального врезания Врs(П7) на высоту зуба. После завершения врезания это движение отключают, и затем в течение одного оборота заготовки колеса профилируют его зубья. Таким образом, линия зуба червячного колеса воспроизводится вращательным движением В1 фрезы. А формообразующая часть кинематической структуры станка для нарезания червячных колес при радиальном врезании должна содержать одну формообразующую группу Фv(В1В2) и группу врезания Врs (П7).
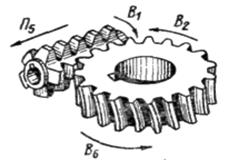
Рис. 3.57. Зубофрезерование при профилировании обкатом: а – цилиндрического прямозубого колеса; б, в – червячного колеса
Более производительной при нарезании червячных колес является схема с касательным врезанием (рис. 3.57,в). В этом случае используют длинные фрезы с заборным конусом. При обработке червячных колес наряду с движением обката фрезе на этапе врезания сообщают движение П5 по касательной к начальной окружности нарезаемого колеса, которое согласовывают с дополнительным движением В6. Таким образом, движение касательного врезания осуществляется сложным движением Вр (П5В6). Как и в схеме с радиальным врезанием, после завершения этапа врезания это движение отключают, и затем в течение одного оборота заготовки профилируют зубья колеса.
Рис. 3.58. Расположение червячной фрезы при зубофрезеровании прямозубого колеса
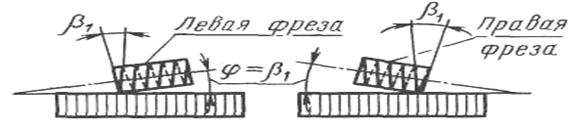
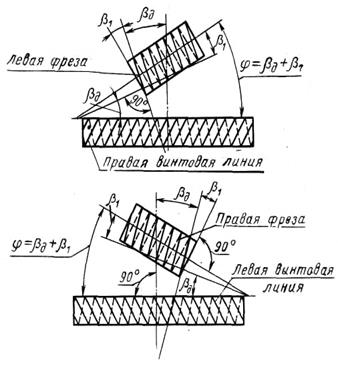
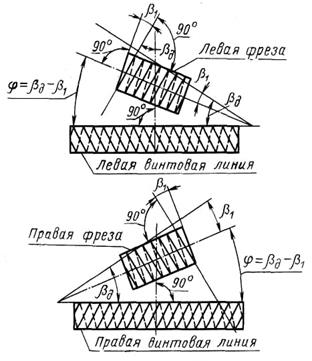
а б Рис. 3.59. Взаимное расположение червячной фрезы и заготовки при нарезании цилиндрического колеса с винтовой нарезкой
Каждая из рассмотренных схем реализуется частной кинематической структурой зубофрезерного станка. Обычно при проектировании станков частные кинематические структуры объединяют в структуру универсального зубофрезерного станка. А выбор конкретной схемы обработки осуществляют соответствующей коммутацией в кинематической схеме станка. При изготовлении станков по индивидуальным заказам под конкретную деталь используют ту или иную частную кинематическую структуру. При зубофрезеровании исходное положение червячной фрезы зависит от заданного положения зубчатого венца на заготовке. При фрезеровании цилиндрических колес с прямыми зубьями (рис. 3.58) червячную фрезу устанавливают под углом φ, равным углу β1 подъема винтовой нарезки червячной фрезы, к торцовой плоскости нарезаемого колеса. При нарезании цилиндрических колес с винтовыми зубьями ось червячной фрезы устанавливают в зависимости от углов наклона винтовых нарезок фрезы и обрабатываемого колеса следующим образом: - если углы наклона винтовых нарезок червячной фрезы β1 и нарезаемого колеса βд одноименны (оба левые или оба правые), то угол установки оси фрезы равен φ = βд – β1 (рис. 3.59,а); - если углы наклона винтовых нарезок червячной фрезы β1 и нарезаемого колеса βд разноименны (фреза левая, а колесо правое и наоборот), то угол установки оси фрезы равен φ = βд + β1 (рис. 3.59,б). Рекомендуется выбирать червячную фрезу с тем же направлением винтовой нарезки, что и обрабатываемого колеса. При нарезании червячных колес ось червячной фрезы устанавливают параллельно торцовой плоскости нарезаемого колеса, т. е. угол φ = 0. Рассмотрим реализацию описанных схем обработки в частных кинематических структурах универсального зубофрезерного станка (рис. 3.60). Выбор конкретной структуры осуществляют при наладке станка посредством соответствующих переключений. Частная кинематическая структура для нарезания цилиндрических колес с прямыми зубьями. Рассматриваемая структура содержит две формообразующие группы: скорости резания (обката) Фv(В1В2) и вертикальной подачи Фs(П3). Группа Фv – сложая. Ее внутренняя связь, называемая цепью обката, профилирования или деления: В1 → 1→ 2 → ∑ → iобк → 3 → 4 → В2. Внешняя связь: М → iv → 2, где 2 – звено соединения связей. Группа настраивается: на траекторию органом настройки iобк, как правило, - это 4-х или 6–и колесная гитара сменных зубчатых колес; на скорость органом iv – это 2-х колесная гитара сменных зубчатых колес, реже простая коробка скоростей. Группа Фs1 – простая. Ее внутренняя связь: вертикальные направляющие стойки – суппорт фрезы. Внешняя связь – кинематическая цепь М → iv → 2 → ∑ → iобк → 3 → is → 6 → 5 → тяговый вал → суппорт фрезы, где суппорт фрезы является звеном соединения связей, а функцию тягового вала выполняет передача вертикальный винт – гайка. Группа настраивается: на скорость органом настройки is (гитара сменных зубчатых колес или простая коробка подач); на путь и исходную точку по упорам системы путевого управления. Обе группы соединены между собой общим электродвигателем и частью передач структурных связей. Во внутренней связи группы обката, часть которой одновременно входит во внешнюю связь группы подачи, расположен планетарный дифференциал ∑. В данной структуре он используется как зубчатая передач.
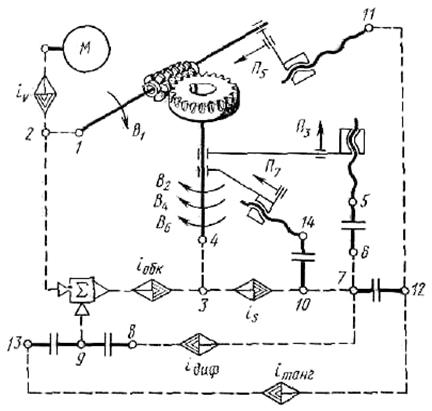
Рис. 3.60. Структурная схема универсального зубофрезерного станка
Выведем ФН для кинематических органов настройки рассматриваемой частной структуры. РП для органа настройки iобк запишем в виде: 1 об. фрезы (В1) → k/z об. заготовки (В2), где к – число заходов фрезы; z – число зубьев нарезаемого колеса. Тогда, УКЦ: k/z = 1 ∙ i01 ∙ i∑в ∙ iобк, где i01 – произведение передаточных отношений передач расчетной цепи (константа конкретной модели станка). Откуда, ФН: iобк = c0 ∙ k/z , где с0 = 1/ i01 ∙ i∑в – константа. РП для органа настройки iv: nМ мин-1 → nф мин-1 фрезы (В1). Тогда, УКЦ: пф = пм ∙ i02 ∙ iv . ФН: iv = пф / i02 ∙ пм, где i02 – константа. РП для органа настройки is: 1 об. заготовки → sв перемещения фрезы (П3), где sв – вертикальная подача фрезы на 1 об. УКЦ: sв = 1 ∙ i03∙ is ∙ tтв, где tтв – шаг тягового вала. ФН: is = sв / i03 ∙ tтв, где i03 ∙ tтв – константа. Встречаются станки, в которых группа вертикальной подачи Фs имеет отдельный электродвигатель М1. В таком варианте орган настройки is устанавливается между кинематическим звеном 6 и электродвигателем М1, и внешняя связь группы становится короче: М1 → is → 6 → тяговый вал → суппорт фрезы. А условие согласования перемещений исполнительных звеньев расчетной цепи, т. е. РП будут иметь вид пм1 мин-1 электродвигателя М1 → sв мм/мин перемещения фрезы (П3) Частный вариант структуры внутренней связи группы Фv (В1В2). При нарезании прямозубых колес с простым числом зубьев встречаются случаи, когда невозможно, при имеющемся наборе сменных колес, точно настроить гитару iобк. Тогда во внутренней связи группы Фv параллельно гитаре iобк посредством планетарного дифференциала ∑ подключается гитара iдиф. В итоге внутренняя связь группы имеет вид В1 → 1 → 2 →∑ → iобк → 3 → 4 → В2 ↑ ↓ 9←iдиф←7←is Рассмотрим особенности вывода ФН для гитар iобк и iдиф для этого случая настройки. Задают zф близкое к z нарезаемому, но удобное для настройки гитары iобк. Настройка гитары iобк по zф дает погрешность ∆z =±( z – zф). Эта погрешность уточняется в зависимости от sв по выражению ∆z = (1/5-1/10)sв. После этого окончательно устанавливают zф = z ± ∆z. Затем выражают z/k через zф. В результате окончательно получают z/k = zф/k ± ∆z/k. По zф/k настраивают гитару iобк, а по ∆z/k гитару iдиф. ФН для гитары iобк имеет вид: iобк = c1 ∙ k/zф. Выведем ФН для гитары iдиф. Расчетная цепь для этой гитары: 1 – 2 - ∑ - 9 – iдиф – 7 – is – 3 – 4. Тогда, РП: 1 оборот фрезы (В1 )→ k/∆z дополнительного поворота заготовки (В2). УКЦ: k/∆z = 1 ∙ i04 ∙ i∑z ∙ is ∙ iдиф. Подставляя в полученное уравнение значение is, после преобразований получим ФН: iдиф = c1 ∙k ∙ sв / ∆z. В формулу входит значение вертикальной подачи sв. Поэтому гитара подач в рассматриваемом варианте настраивается точно. Частная кинематическая структура для нарезания цилиндрических колес с винтовым зубом. Данная структура содержит две сложных группы: скорости резания (обката) Фv(В1В2) и вертикальной подачи Фs1(П3В4). При рассмотрении способов обработки зубчатых колес было отмечено, что во всех вариантах профилирование зубьев осуществляется одной и той же группой Фv. Эта группа рассмотрена при описании предыдущей частной структуры. Группа Фs(П3В4) – сложная, двухэлементарная. Ее внутренняя связь: П3 → ТВ → 5 → 6 → 7 → iдиф → 8 → 9 → ∑ → iобк → 3 → 4 → В4. Внешняя связь: М → iv → 2 → ∑ → iобк → is → 7. Группа настраивается на траекторию – гитарой iдиф, на скорость – гитарой или простой коробкой подач is, на путь и исходную точку по упорам системы управления. В рассматриваемой структуре делительный стол заготовки является исполнительным звеном обеих формообразующих групп. Поэтому внутренние связи обеих групп соединены планетарным суммирующим механизмом ∑, осуществляющим физическое сложение движений В1 и В4. Выведем ФН для органов настройки iдиф и is. Расчетная цепь для гитары iдиф совпадает с внутренней связь группы. Поэтому РП для расчетной цепи, называемой цепью дифференциала, обеспечивающей согласование перемещения фрезы вдоль заготовки с ее дополнительным вращением, записываются в виде: T мм перемещения фрезы (П3) → 1 об. заготовки (В4), где T – шаг винтовой линии зуба колеса. Тогда, УКЦ: 1 = T/tТВ ∙ i04∙ iдиф∙ i∑z ∙ iобк . Откуда, ФН: iдиф =c2/T ∙ iобк , где с2 = tТВ / i01∙ i∑z – константа. В полученном выражении для ФН заменим Т и iобк их значениями. Из развертки зубчатого колеса с винтовым зубом
где ms – модуль осевой; mn – модуль нормальный; z – число зубьев нарезаемого колеса; β – угол наклона винтового зуба. После замены, окончательно получим
По полученной ФН предаточное отношение iдиф вычисляют с точностью до пятого знака после запятой. Расчетная цепь для органа настройки is такая же, как и при нарезании прямозубых колес. Поэтому, полученная в соответствующей структуре ФН, используется также и в рассматриваемой частной структуре. Частная кинематическая структура для нарезания червячных колес при радиальном врезании. Данная структура содержит общую для всех рассматриваемых частных структур группу обката Фv (В1В2), воспроизводящую профиль зубьев, и простую группу радиального врезания Врs (П7) на высоту зубьев. Внутренняя связь группы радиального врезания: горизонтальные направляющие → стол или стойка суппорта (П7) Внешняя связь: кинематическая цепь, связывающая электродвигатель М со звеном соединения связей (стол или стойка суппорта), т. е. М → iv → ∑ → iобк → is → 10 → 14 → ТВ (П7). Группа настраивается на скорость (радиальную подачу) – общим для всех, рассматриваемых частных структур, органом настройки is, на путь и исходную точку по упорам системы управления. Выведем ФН для органа настройки is. Расчетная цепь, называемая цепью радиальных подач, 4 - 3 – is - 10 – 14 – ТВ. РП: 1 об. стола → sр перемещения стойки суппорта (П7), где sр – радиальная подача на 1 об. УКЦ: sр = i05 ∙ is ∙ tТВ. ФН: is = sр / i05 ∙ tТВ = c3 ∙ sр, где c3 = 1/i05 ∙ tТВ - константа. Частная кинематическая структура для нарезания червячных колес при тангециальном (осевом) врезании. Эта структура содержит рассмотренную выше группу формообразования Фv. Поэтому рассматрим только кинематическую группу тангенциального, или осевого врезания Вро (П5В6 ). Эта группа сложная двухэлементарная, обеспечивающая функциональную связь между осевым перемещением П5 и дополнительным поворотом заготовки В6. Ее внутренняя связь: П5 → 11 → 12→ iтанг → 13 → 9 →∑ → iобк → 3 → 4 → В6. Внешняя связь: М → iv → ∑ → is→ 12. Планетарный дифференциал ∑ является звеном соединения связей. Группа настраивается на траекторию – гитарой iтанг, на скорость – органом настройки is, на путь и исходную точку – упорами системы управления. Выведем ФН для обоих органов настройки группы. Гитара сменных колес iтанг. Расчетная цепь совпадает с внутренней связью. Поэтому РП: L тангенциального перемещения фрезы (П5)→L/πmz об. заготовки (В6). Тогда, УКЦ: В полученное уравнение входит иррациональное число π, и шаг тягового вала tТВ. Поэтому винт тангенциального перемещения протяжного суппорта фрезы, с целью устранения иррацианальности при определении передаточного отношения гитары iдиф, изготавливают с модульной резьбой. Учитывая это обстоятельство, а также заменяя передаточное отношение iобк его значением, полученным при рассмотрении кинематической структуры для нарезания прямозубых колес, после элементарных преобразований, получим ФН: iтанг = c4 k m, где с4 –константа; k – количество заходов фрезы; m - модуль. Орган настройки is: Расчетная цепь, включающая орган настройки, связывает делительный стол заготовки с тяговым валом тангенциального перемещения фрезы. Тогда, РП: 1 об. заготовки → sо перемещения фрезы (П5), где sо – тангенциальная подача на 1 об. УКЦ: sо = 1· i07 · is · tТВ ФН: is = c5 ∙ sо, где c5 – константа. Кинематическая структура для нарезания червячных колес при тангенциальном врезании используется, преимущественно, в крупносерийном и массовом производствах. Здесь наиболее полно проявляются преимущества такого способа обработки – больший период стойкости фрезы и повышенная точность обработки. Объясняется это тем, что зубья фрезы, расположенные на заборном конусе, срезают основную часть металла заготовки. При нарезании цилиндрических колес с винтовым зубом и червячных колес при тангенциальном врезании делительный стол заготовки совершает суммарное вращение соответственно В2 ± В4 или В2 ± В6 , так как является исполнительным звеном одновременно работающих двух исполнительных групп. Два движения на одном исполнительном звене физически складываются планетарным дифференциалом. Поэтому кинематическую структуру зубофрезерных станков, имеющих дифференциалы, и их кинематическую настройку называют дифференциальными. В обоих вариантах слагаемые элементарные движения имеют одинаковую скоростную характеристику, продолжительность их одинакова и создаются они одним источником движения. Движения, удовлетворяющие названным условиям можно складывать математически без дифференциала. Поэтому указанные виды колес можно нарезать также на зубофрезерных станках, не имеющих дифференциалов и соответственно внутренних связей с органами настройки iдиф и iтанг, воспользовавшись методом математического сложения движений при бездифференциальной настройки. Сущность этого метода сводится к тому, что условия кинематического согласования перемещений исполнительных звеньев расчетных цепей с гитарами iдиф и iтанг учитываются в расчетных перемещениях цепи обката с гитарой iобк. При нарезании цилиндрического колеса с винтовыми зубъями РП будут иметь вид: 1 об. заготовки (В1) → а при нарезании червячного колеса при тангенциальном врезании 1 об. заготовки → Знаки ″+″ или ″–″ берут в зависимости от сочетания направлений винтовых линий на нарезаемом колесе и фрезе. Пример бездифференциального станка – шлицефрезерный станок модели 5350, на котором можно нарезать шлицевые валы и зубчатые колеса с прямыми и винтовыми шлицами и зубьями. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
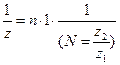 .
.
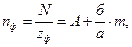
 .
.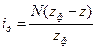 .
. .
. .
.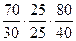 .
. При делении, поворачивая рукоятку на установленные посредством раздвижного сектора 40 отверстий на лимбе с 60 отверстиями, шпиндель с заготовкой повернется на 1/67.
При делении, поворачивая рукоятку на установленные посредством раздвижного сектора 40 отверстий на лимбе с 60 отверстиями, шпиндель с заготовкой повернется на 1/67. tg α = π D/tк.,
tg α = π D/tк.,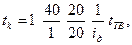

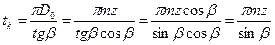 ,
, 
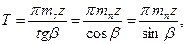
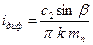 .
.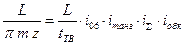 .
.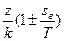 об. фрезы (В2),
об. фрезы (В2), об. фрезы (В2).
об. фрезы (В2).