
|
|
Общий, средний и предельный продуктПроизводство — основная область деятельности фирмы. Для получения продукции в процессе производства используются различные экономические ресурсы, производственные факторы. Зависимость между вводимыми факторами, производственным процессом и выпуском продукции описывается при помощи производственной функции. Производственная функция показывает максимальный объем выпуска продукции, который фирма может произвести при каждом сочетании факторов производства. Производственная функция отражает различные способы соединения производственных факторов для выпуска определенного объема продукции и применима к определенной технологии производства. Если технология улучшается, то при том же наборе факторов производства фирма может увеличить объем выпуска. Условие «максимальный объем выпуска» является очень важным и означает, что не допускается технологическая и экономическая неэффективность фирм. Производственная функция учитывает только технологически эффективные варианты. Способ производства технологически эффективен, когда производимый объем продукции является максимально возможным при использовании данных объемов ресурсов (т. е. никогда не применяются такие комбинации ресурсов, которые снижают объем выпуска). Конечно, предположение о том, что производство технологически и экономически эффективно, не всегда справедливо, но для фирм, стремящихся к максимальной прибыли, достаточно реалистично — они не будут расходовать ресурсы впустую. Фирмы постоянно корректируют производственные процессы и свое поведение на рынке, пытаясь найти наиболее оптимальные варианты. Если предположить, что имеются только два вводимых фактора производства — труд L и капитал К, то производственную функцию можно записать так: Q = f (L, К). Наиболее известна производственная функция Кобба-Дугласа, задающая объем выпуска Q в зависимости от затрат L и К: Отметим, что построение производственной функции исходит из допущения, что фирма выпускает однородный продукт и использует однородные ресурсы. Если мы подразделяем труд по профессиям и квалификации, капитал по составу, сырье по сортам и т. д., то мы имеем дело с различными ресурсами, и производственная функция становится от большого числа переменных. Для построения производственной функции важное значение имеет период, в течение которого фирма может отреагировать на перемены в рыночной ситуации и изменить объем или даже состав производства. Будем считать капитал фиксированным фактором, а труд — переменным. Фирма может менять объем производства, изменяя количество труда (продолжительность рабочего времени или численность работников). Для характеристики зависимости между затратами фактора производства (труда) и объемом выпуска используются понятия общего, среднего и предельного продукта (рис. 2.1).
Рис. 2.1. Кривые общего, среднего и предельного продукта
Общий продукт ТР — максимальный объем продукции, выпускаемый при данном количестве производственных факторов. Кривая ТР (график производственной функции) показывает зависимость между затратами переменного фактора L и объемом выпуска (при фиксированном К). Средний продукт АР любого ресурса L (труда) — это объем выпуска продукции, приходящийся на единицу используемого фактора: Это показатели производительности ресурсов. Средний продукт труда часто называют производительностью труда. Предельный продукт МР любого переменного фактора (труда) представляет собой дополнительный объем выпуска, полученный за счет использования дополнительной единицы данного фактора:
Когда объем труда L = 0, то выпуск Q = 0. При увеличении затрат труда выпуск продукции растет, но до определенного предела, выше которого дополнительные затраты труда приводят к снижению Q. Эта часть кривой ТР изображается пунктиром, так как производство при таких затратах становится неэффективным. Кривая АР также сначала растет, достигает максимума, а затем начинает снижаться. Кривая МР ведет себя подобным образом. МР > 0 всегда, когда Q увеличивается, и МР < 0, когда Q уменьшается. Выделяются три стадии динамики ТР, АР и MР. 1. Объем выпуска ТР растет быстрее, чем повышаются затраты. 2. Объем выпуска увеличивается медленнее, чем растут затраты. 3. Дальнейший рост затрат ведет к снижению Q. Существует тесная зависимость между АР и МР. Когда МР > АР (первая стадия), АР увеличивается (увеличивается производительность труда), когда МР < АР > О, АР снижается (снижается производительность труда, хотя общий выпуск еще растет). Когда МР = АР, кривая АР достигает максимума. Имеется и четкая геометрическая взаимосвязь между кривыми ТР, АР и МР. АР в каждой точке кривой ТР измеряется наклоном луча, идущего от начала координат в эту точку. Средний продукт АР достигает максимума в точке С, где луч имеет наибольшую крутизну. Предельный продукт МР геометрически в каждой точке на кривой ТР равен углу наклона касательной, проведенной через данную точку. Сравнивая угловые коэффициенты касательных к кривой ТР, можно увидеть, что сначала МР растет, достигает максимума в точке В, а затем снижается до точки D. Когда Q достигает максимума, наклон касательной к кривой ТР = 0 и МР = 0, после чего МР < 0. Из этих зависимостей следует, что фирме целесообразно наращивать объем выпуска до точки D, т. е. до того момента, пока приращение фактора производства (хi, L) ведет к приращению объема производства. Фирме предпочтительнее находиться во второй стадии кривой ТР. Тенденция к сокращению МР (как и других факторов) является настолько преобладающей, что о ней говорят как о законе убывающей производительности (убывающей отдачи): по мере роста затрат любого переменного фактора при фиксированных затратах остальных факторов неизбежно наступает момент, когда дополнительное использование переменного фактора будет приносить все меньший вклад в выпуск продукции. Данный закон применим к определенной технологии, и действует в краткосрочном периоде, т. е. не является универсальным. Его абсолютизация лежала в основе теории народонаселения Т. Мальтуса. Если нет ограничений на вводимые ресурсы (в долговременном периоде), то действуют иные закономерности.
Изокванты и изокосты. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
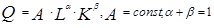 .
.
 .
.
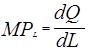 .
.