
|
|
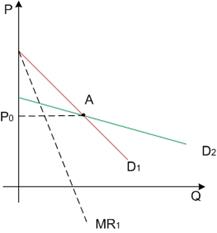
Жёсткость цен и ломаная кривая спроса.В первой половине XX в. считалось, что на олигополистических рынках у цен существует тенденция быть жёсткими (неизменными). В 30–х гг. Пол Суизи разработал модель, которая бы смогла объяснить, почему на олигополистических рынках цены редко изменяются. Пол Суизи в 1939 г. опубликовал статью «Спрос в условиях олигополии», где проанализировал сталеплавильную промышленность США, в которой в течение 10–х – 20–х гг. ХХ века цена стали оставалась неизменной даже несмотря на увеличение средних издержек. На основе этих наблюдений он развил модель, демонстрирующую весьма необычный вид кривой спроса фирмы, работающей на рынке олигополии. Модель иллюстрирует условия цены при олигополии. Ее допущения: 1. фирмы производят дифференцированные продукты; 2. фирмы предполагают , что соперник не станет повышать цены вслед за ней, поскольку это ведет к потере покупателей, а в случае уменьшения данной фирмой цены конкуренты предпримут аналогичные действия и тогда данная фирма становится не способной привлечь доп. кол-во участников; 3. фирма максимизирует прибыль, производя такое кол-во товаров, при котором МR=МС. Предположим, что на рынке установилась цена .p. Заметим, что модель не объясняет, каким образом эта цена установилась. Она просто принимает этот факт как данность. Если какая-либо фирма увеличивает цену на свою продукцию (и, причём, делает это в одностороннем порядке), тогда другие фирмы в отрасли не последуют её примеру. В результате этого она потеряет часть своей рыночной доли, поскольку покупатели переключаются на продукцию тех фирм, у которых относительно более низкие цены. Если же фирма, напротив, снизит цену, то это может спровоцировать снижение цен другими фирмами в отрасли, чтобы избежать потери доли рынка, которая может отойти фирме с более низкой ценой. Из-за того, что в этом случае конкуренты последуют за данной фирмой, спрос на её продукцию окажется менее эластичным. Допустим, что на отраслевом рынке конкурирует три фирмы. Рассмотрим реакцию 2 и 3 фирм на поведение 1-ой фирмы. Возможны 2 ситуации: · фирма 1 повышает цену; · фирма 1 понижает цену. В случае, если 1 фирма 1 цену выше P0, ее спрос изображается кривой D1, выше уровня P0. Конкуренты, т.е. фирмы 2 и 3 не будут за ней следовать и их цены останутся либо неизменными либо вырастут в гораздо меньшей пропорции как показ. кривая D2, лежащая так же выше.
Рисунок 11 – Ломаная кривая спроса олигополиста Фирма 2 предпочитает либо не следовать за фирмой 1. D2 - D1 – ломанная кривая. Если фирма 1 понижает цену ниже уровня P0 фирмы 2 и 3, будет следовать за ней и это показывает линия D1, лежащая ниже P0. В результате, возникновения ломанная кривая спроса D2 - D1 высокоэластичная, выше уровня P0 и малоэластичная, ниже ее. Предложенная модель объясняет относительную негибкость (жесткость) цен при олигополии, т.е. любое повышение цен ухудшает ситуацию, а именно - повышение цены одной фирмой позволит захватить рынок конкурентами, которые могут переманить прежних покупателей фирмы, сохраняя низкие цены. Аналогично и при повышении цены. Конкуренты точно так же могут повысить цены, сохраняя свою долю на рынке, что не приведет к росту объема продаж. В результате, лидирующая фирма не сможет увеличить число покупателей за счет других фирм. В результате возможна «ценовая война». Конечно, данная модель мало полезна для принятия стратегических решений, потому что она статична. Она также не объясняет сам процесс ценообразования на рынке олигополии. Но она объясняет, почему фирмы-олигополисты очень часто не склонны изменять цены на свою продукцию: изменение цены в данном случае просто приведёт к сокращению прибыли. Это объясняет, почему в периоды общих экономических спадов производства цены на олигополистических рынках не снижаются столь стремительно, как на более конкурентных рынках. Не повышаются они и при незначительном увеличении средних издержек. Только очень сильное повышение (значит, и AC)MC в данной модели может повлечь за собой увеличение цены.
Одновременные олигопольные игры. Модель дуополии Курно и модель Бертрана. Особенность этого типа стратегического поведения состоит в том, что фирмы-олигополисты действуют одновременно и, следовательно, ни одна из фирм, принимая собственное решение об установлении цены или объёма выпуска, не знает точно, как поведут себя другие фирмы – её конкуренты. Таким образом, каждая фирмы должна угадать, какую цену назначат её конкуренты или какой объём продукции они произведут. Здесь необходимо проводить различие между олигополистическими рынками, на которых фирмы определяют количества, и рынками, на которых фирмы устанавливают цены. Сначала мы введём модель, называемую конкуренцией по Курно, в которой выбираются уровни производства, а затем рассмотрим модель Бертрана, в которой фирмы конкурируют при помощи цен. Модель дуополии Курно Данная модель строится на следующих предпосылках: 1. Две фирмы производят однородный товар. 2. Фирмам известна кривая рынка спроса. 3. Фирма принимает решение о производстве независимо друг о друга товара. 4. Каждая из фирм предполагает выпуск конкурента постоянным или заданным. Суть модели Курно заключается в том, что каждая фирма принимает объём производства своего конкурента постоянным, а затем принимает собственное решение по объёму производства. При этом и та, и другая фирма стремятся к максимизации собственной прибыли. Рассмотрим следующую задачу: Предположим, что функция рыночного спроса представлена в виде: Q=60-P. На рынке работают 2 фирмы, т.е. Q =q1+ q2 Общие издержки фирм равны соответственно: ТС q1=6 q1+5, ТС q2=0,5 q2+1 Необходимо найти Q q1=? Q q2=? Qобщ =? Р=? πq1=? πq2=? =? πобщ =? Решение: Первоначально необходимо исчислить прибыль каждой фирмы и оценить ее максимальную величину. π1=TR-TC1→60 - ( q1+ q2)∙ q1-6 q1+5 π2=TR-TC2→60 - ( q1+ q2)∙ q2-0.5 q2+5 TR= ТQ Из Qd →P=60-Q TR1= ТQ1 P = 60 – (q1+ q2) TR2= ТQ2 Предполагая внутренний оптимум для каждой фирмы, мы получаем условие первого порядка MR=MC→ π' = 0
q1 =
q2 = Кривая реакции каждой фирмы показывает, как изменяется максимизирующий прибыль объём производства одной фирмы в зависимостиот того, как, по её мнению, будет расти объём выпуска другой фирмы. Каждая фирма устанавливает объём выпуска в соответствии с собственной кривой реакции, и поэтому равновесный уровень выпуска находится на пересечении двух кривых реакции. Составляет систему уравнений, и рассчитываем объем производства у каждой фирмы.
q1 = 20,4 q2 = 13,2 Р=24,6 π1 = 411,16, π2= 263,36, π3 = 674,52. В условиях взаимодействия фирм по Курно формируются равновесия q1 = объем выпуска 1 фирмы q2 = объем выпуска 2 фирмы В этой модели две фирмы одновременно стараются решить: какое количество продукции им производить? Здесь каждая фирма должна предвидеть, какой выпуск продукции у другой фирмы, чтобы принять решение относительно собственного выпуска. Предвидя тот или иной выпуск другой фирмы, данная фирма в зависимости от этого выбирает свой собственный выпуск, максимизирующий её прибыль. Следовательно, равновесие в модели Курно достигается, когда обе фирмы правильно оценивают возможный выпуск конкурента и поэтому с успехом максимизируют свои собственные прибыли (т.е. одновременно выбирают оптимальные объёмы выпуска). Модель Бертрана В модели Курно конкурирующие фирмы принимают решения об уровнях производства, но не о ценах. Один из главных упрёков к модели Курно состоит в том, что в действительности фирмы скорее выбирают стратегии изменения цен, а не производства. Спустя пятьдесят после первой публикации работы Курно Жозеф Бертран выступил с критикой её концепции именно с этих позиций. С тех пор конкуренция по ценам на олигополистических рынках называется конкуренцией Бертрана. Согласно этой модели дуополисты вырабатывают решение независимо друг от друга, принимают уровень цены конкурента как данный и при этой предпосылке выбирают решения от уровня своей цены. В модели Бертрана на рынке действуют две фирмы, производящие однородный продукт. Обе фирмы одновременно устанавливают цены на свой продукт. Если цены фирм различаются, то естественно предположить, что потребитель будет покупать продукт у фирмы, имеющей более низкие цены. Если две фирмы установят одну самую низкую цену, то половина покупателей будет брать товар одной фирмы, а вторая половина – другой. Предполагается, что мощности фирм достаточны, чтобы удовлетворить потребности покупателей даже при наиболее низкой цене и что не существует нерациональных потребителей. Предельные издержки фирм постоянны и равны друг другу. Каждая фирма выбирает цены так, чтобы максимизировать свою прибыль. На языке теории игр владельцы фирм являются игроками, устанавливаемые цены – стратегией, а прибыли – выигрышами. В модели Бертрана рассматривается «ценовая вышка» - цена постепенного смещения существующего уровня цен с целью вытеснения конкурентов с олигопольного рынка. Она продолжается до тех пор, пока цена не снизится до уровня АС. Т.е. в целях равновесия будет выполняться равенство: МС=АС=Р Фирмы выбирают свои цены одновременно и несогласованно. Одновременность означает, что каждая фирма ещё не знает о цене другой фирмы, когда выбирает свою собственную цену. Равновесие Бертрана– это пара цен такая, что цена каждой фирмы максимизирует прибыль фирмы при данной цене другой фирмы. Выводы из этой модели действительно поражают: фирмы назначают цену на уровне предельных издержек и фирмы не получают прибыль. Эти заключения подразумевают, что даже наличие дуополии могло бы быть достаточным для восстановления совершенной конкуренции. Экономисты называют это парадоксом Бертрана, так как трудно предположить, что в отраслях с небольшим числом фирм последним не удастся манипулировать рыночной ценой для того, чтобы получить прибыль. Конкурентные ситуации по Курно и по Бертрану приводят к различным равновесным уровням прибыли. В модели Курно фирмы получают положительные прибыли. В стандартной модели Бертрана фирмы, имеющие одинаковые предельные издержки, вообще лишены возможности получения положительной прибыли. Таким образом, конкуренция по ценам более жёсткая, чем конкуренция по количествам. В модели Бертрана для двух компаний, фирма, которая установила более высокие цены, вообще останется без прибыли, в то время как в модели Курно положительные прибыли будут иметь обе фирмы, производящие разные количества товара. Поскольку различие слишком существенно, то очень важным представляется вопрос, какая из двух моделей ближе к реальности? На большинстве рынков компании принимают решения как относительно цен, так и относительно количеств и поэтому не всегда очевидно, какую модель необходимо использовать. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 = 0
= 0 = 0
= 0 - уравнение реакции первой фирмы на объем производства второй фирмы
- уравнение реакции первой фирмы на объем производства второй фирмы - уравнение реакции второй фирмы на объем производства первой фирмы
- уравнение реакции второй фирмы на объем производства первой фирмы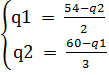
 = 0;
= 0;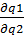 = 0;
= 0;