
|
|
Понятие измерения в социологии. Уровни измеренияОпределение измерения. Измерением называется процедура, с помощью которой объекты измерения, рассматриваемые' как носители определенных соотношений, отображаются в некоторую математическую систему с соответствующими отношениями между элементами этой системы. В качестве объектов измерения могут выступать респонденты, производственные коллективы, условия труда и быта и т. д. В отношения, которые моделируются'при измерении, объекты вступают как носители определенных свойств. Так, мы можем рассматривать респондентов изучаемой совокупности как носителей такого свойства, нак удовлетворенность своим трудом, и рассматривать отно- 1 Лафарг П. Воспомипания о Марксе. Ml, 1959, с. 6. ' Плеханов Г. В. Иэбр. ф-лос. произв. М., 1966, т. 1, с. 537. 4 Ленин В. И. Поли. собр. соч., т. 18, с. 164. * Тамже, т. 29, с. 471. шепие равенства между ними, считая каких-то респондентов «равными» или «неравными» в зависимости от степени рассматриваемой удовлетворенности. Те же респонденты могут выступать как носители .такого свойства, как «возраст». Ясно, что между «ими может быть определено отношение равенства, однако респоп-денты, «равные.» друг другу в первом случае, могут оказаться «неравными» во втором. Каждому объекту при измерении приписывается определенный элемент используемой математической системы. В социологии чаще всего используются числовые математические системы, т. е. та,кно системы, элементами которых являются действительные числа. Однако возможно эффективное использование и нечисловых математических систем1: частично упорядоченных множеств, графов,-матриц и т. д. Адекватное измерение предполагает наличие общего представления о наблюдаемых объектах, об их изучаемых сторонах. Такое представление даст возможность выделить отношения между объектами, которые должны отображаться в соответствующие отношения между элементами использующейся математической системы2. Поскольку при практическом осуществлении измерения социологи ь подавляющем большинстве случаев используют числовые системы, остановимся на принципах их применения в социологии. Будем называть шкалой тот алгоритм, с помощью которого каждому наблюдаемому объекту ставится в соответствие некоторое число. Приписываемые же объектам числа назовем шкальными значениями этих объектов. Элементы используемых в социологии числовых систем, как правило, нельзя считать «полноценными» числами. Приведем пример. Предположим, что нас интересует отношение порядка между респондентами по их .удовлетворенности своим трудом. Пусть процесс измерения состоит в следующем. Мы задаем каждому респонденту вопрос: «Удовлетворены ли Вы своим трудом?» с традиционным веером из пяти ответов (от «совершенно не удовлетворен» до «вполне удовлетворен»). Каждому ответу присвоим соответственно числа от 1 до 5. Ясно, что реальным отношениям между респондентами в таком случае отвечает лишь отношение порядка между числами. Другие же операции под этими числами, например их 1 См., например: Воронов Ю. П., Ершова П. //. Общие принципы социологического измерения.— В кн.: Измерение и моделирование в социологии. Новосибирск, 1909, с. 3—15; Хованов И. В. Математические основы теории шкал измерения качества. Л., 1982; Лааарсфелъд П. Ф. Измерение в социологии.— В ки.: Американская социология. М., 1972, с. 134—149. * Выделяя интересующие нас свойства изучаемых объектов, абстрагируясь от бесконечного количества их других свойств, получаем определенную модель реальности. В теории измерения для обозначения подобной модели используется термин «эмпирическая система с отношениями» (см., например: Суп-пес П., Зинес Дж. Основы теории измерений.— В ки.; Психологические измерения. М., 1967, с. 9-110). сложение, пе имеют эмпирически иптерпретируемого смысла. Другими словами, полученные шкальные значения не являются числами и обыденном значении этого понятия. Встает естественный вопрос: какими известными соотношениями между числами мы в подобных ситуациях можем пользоваться, чтобы, анализируя шкальные знамения, можно было получать содержательные выводы? Для ответа на этот вопрос необходимо в первую очередь четко представить себе характер числовых систем, использующихся в процессе измерения в социологии. Неоднозначность шкальных значений. Допустимые преобразовав ния и типы шкал.Единственное требование, предъявляемое к числам, служащим шкальными значениями, состоит в том, что рассматриваемые эмпирические отношения должны переходить в соответствующие им числовые отношения. Этого требования, как правило, бывает недостаточно для однозначного определения множества шкальных значений. Совокупности величин, полученпых по используемым в социологии шкалам, обычно бывают определены лишь с точностью до некоторых преобразований этих величии, которые называются допустимыми преобразованиями соответствующих шкал.' В соответствии со сложившейся в литературе традицией тип шкалы определяется соответствующим этой шкале множеством допустимых преобразований. Чтобы пояснить введенные определения, опишем типы наиболее часто использующихся в социологии шкал. Шпалы наименований (поминальные, классификационные). При использовании шкалы наименований объекты измерения распадаются на множество взаимно исключающих и исчерпывающих классов. Каждому классу дается наименование, числовоо обозначение которого является одним из шкальных зиачешш. Шкала наименований получается, если в качестве моделируемых в процессе измерения эмпирических отношений выступают лишь отношения равенства инеравенства между объектами. Требования, предъявляемые к шкальным значениям, состоят в том, что равным объектам должно соответствовать одно и то же число, а неравным — равные числа. Поэтому поминальная шкала фактически задает некоторую классификацию исходных объектов. Одип класс — это совокупность объектов, имеющих одно и то же шкальное значение. Номинальные шкалы можно определить как шкалы, допусти-мыми преобразованиями которых являются произвольные взаимно однозначные преобразования', т. е. преобразования, сохраняющие отношения равенства и неравенства между числами. Изучаемые эмпирические отношения одинаково хорошо будут отражать, например, следующие совокупности шкальных значений: (1, 1, 2, 3, 4) и (15, 15, 14,13, 12). Каждая из этих совокупностей получена из другой с помощью некоторого однозначного преобразования.
Отметим, что даже при таком простейшем измерении к построению шкалы надо подходить с большой осторожностью. Получаемые классы должиы иметь социологическую значимость. Ясно, что сначала исследователь доджей решить, что он будет классифицировать, какие категории будут при этом исследоваться. Например, если изучаются респонденты как носители определенной профессии, то классифицировать их нужно по принадлежности к той или иной профессии. Предполагается, что каждой профессии произвольно приписывается число, причем разным профессиям соответствуют разные числа. Однако уже здесь проблема измерения (т. е. приписывания респондентам определенных чисел) не столь проста. Нельзя с предельной четкостью выделить всевозможные профессии или по крайней мере считать, что все профессии взаимно исключают друг друга. Например, неизбежно придется столкнуться с таким частный случаем, когда профессия будет комбинацией нескольких. И тогда встанет вопрос о соотнесении респондента, имеющего такую профессию, с некоторой группой профессий и обозначении ее числовым низком. Порядковые шкалы (шкалы порядка). Порядковая шкала получается, если при осуществлении измерения моделируются не только эмпирические отношения равенства и неравенства между изучаемыми объектами, но и отношения порядка между ними. Порядковая шкала не только задает некоторую классификацию на множестве объектов, но и устанавливает определенный порядок между классами. Порядковые шкалы можно определить как шкалы, в качестве допустимых преобразований которых выступают произвольные монотонно возрастающие преобразования*. Последние образуют подсовокупность всех взаимно однозначных преобразований, включающую те из них, которые сохраняют отношение порядка между числами. Примером совокупностей шкальных значений, получающихся друг из друга с помощью некоторого монотонно возрастающего преобразования, могут служить совокупности (1, 3, 5, 4, 2) к (18, 20, 28, 24, 19). Интересующие нас отношения равенства, неравенства и порядка между объектами с одинаковым успехом отражены в.любой из этих совокупностей. Ясно, что порядковые шкалы образуют подмножество номинальных шкал. Пример порядковой шкалы мы получим, если будем различать людей данной профессии по квалификации (сложности труда и т.д.). На практике часто не удается полностью упорядочить объекты изучаемой совокупности относительно того или иного интересующего исследователя свойства. Предположим, например, что изучается совокупность людей носителей свойства «удовлетворенность специальностью», а более узко — свойства, содержащегося в вопросе 4 Монотонно возрастающим называется такое преобразование g(x), которое ' удовлетворяет условию: если z* < х2, то g(xi) < g(xz) для любых чисел х\ и xi из области определения g{x). 14* «Удовлетворены ли Вы своей специальностью?» и пяти ответах на него от «полностью удовлетворен» до «совсем не удовлетворен». Обычно считается, что любую совокупность людей можно упорядо^-■чить в отношении данного свойства, т. е. что ответившие «специальностью полностью удовлетворен» выше по измеряемому качеству, чем те, кто ответил, что «специальностью удовлетворен» и т. д. Зачастую предполагаемого четкого различения оценок не паблю-дается и респонденты не могут однозначно выбрать тот или иной ответ. В этом случае на помощь могут прийти частично упорядоченные множества. Шкальные значения, полученные по порядковой шкале, част» называют рангами. Интервальные шкалы (шкалы интервалов). Интервальные шкалы получаются, если в процессе измерения мы моделируем не только те отношения, которые моделируются при использовании порядковой шкалы, но и отношение равенства (или, что одно и то же, порядка) для разностей (интервалов) между изучаемыми объектами. Далеко не всегда в тех случаях, когда удается построить порядковую шкалу, удается построить и интервальную. Например, возьмем классификацию рабочих по разрядам. Известно, что первый разряд ниже второго, второй — третьего и т. д. (и это соответствует определенному эмпирическому отношению порядка между респондентами), т..е. разряды отвечают порядковой шкале. Однако сопоставлять дистанции между каждой парой разрядов все же нельзя. Интервальным шкалам соответствуют положительные линейные преобразования", т. е. такце преобразования, которые наряду с отношениями равенства, неравенства и порядка между числами сохраняют и отношения равенства и порядка между их разностями (пли, что то же самое, частное от деления любой такой разности на любую другую). -Примером совокупности чисел, получающихся друг из друга с помощью положительного линейного преобразования (у — Зх + 9), служат совокупности (5, 5, 2, 1, 2) и (24, 24, 1Г>, 12, 15). Нетрудно проверить, что в этих совокупностях отражаются одни н те же отношения равенства, неравенства и порядка как дли чисел, так и для интервалов между ними (так, для первой совокупности 5 — 2 > 2 — 1, а для соответствующих шкальных значений и» второй совокупности 24—15> 15 — 12). Легко видеть также, что частные от деления величины одного интервала между шкальными значениями на величину другого не зависят от того, какую и;« рассматриваемых шкал мы выбираем (так, верно соотношение 5-2 24-15 ,, „ унт ~ шкал. Ясно, что положительные линейные преобразования являются подсовокупностью монотонно возрастающих преобразовании, а совокупность интервальных шкал — подмножеством шкал порядка.
Главная трудность при построении интервальных шкал в социо* логии состоит в обосновании равенства или разности дистанций между объектами. Процедуры, позволяющие таким образом преобра-яовать шкальные значения порядковой шкалы, что равенство (порядок) расстояний между полученными числами можно будет трактовать как отражение соответствующего равенства (порядка) ♦расстояний» между изучаемыми объектами, носят название метризации шкалы (или «оцифровки» шкальных значений)". На практике известно много методов шкалирования, позволяющих получать интервальную шкалу «косвенным» образом, без отображения указан-лого отношения непосредственно в процессе измерения'. Шкалам отношений соответствуют положительные преобразовав пия подобия', составляющие подсовокупность положительных линейных преобразований, оставляющих беэ изменения отношения между числами (под отношением здесь понимается частное от деления одного числа на другое). Шкалу отношений получим, если будем требовать, чтобы в процессе измерения не только отношения между эмпирическими объектами отображались в соответствующие числовые отношения, но и один и тот же объект отображался в 0. Подобная возможность иногда возникает в социологических исследованиях. Так, при изучении удовлетворенности респондентов своим трудом, вероятно, в качестве такого объекта имеет смысл выбрать респондента, равнодушного к своей работе. Фиксацию такого нулевого объекта можно рассматривать как задание начала отсчета шкальных значений. Поэтому можно сказать, что шкалы отношений образуют подмножество интервальных шкал, характеризующееся фиксацией начала отсчета. Неоднозпачность совокупности шкальных значений, полученных с помощью измерения по шкале отношений, иллюстрируется примером следующих двух совокупностей, отражающих' одни и те же эмпирические отношения равенства, неравен* ства и порядка как между респондентами, так и между соответствующими интервалами и, кроме того, отвечающих одному и тому же пачалу отсчета (один и тот же объект (второй) в обоих случаях отображается в 0): (2,0,-1,4,1) и (3,0,-3/2,6,3/2). Легко видеть также что для обеих совокупностей частные от деления между шкальными значениями любых пар объектов одни и те же (2:4== = 3:6 и т. д.). Ясно, что рассматриваемые совокупности получаются друг из друга с помощью некоторого положительного преобразования подобия {у = 3/2х). • См.: Типология и классификация в социологических исследованиях/Отв. ред. В. Г. Андреенков, 10. Н. Толстова. М., 1982, гл. IV, § 2. ' Сюда относятся, например, способы построения интервальной шкалы с- помощью метода парных срапнений, известные методы шкалирования Тер- стоуна и т. д. Ряд подобных методов будет рассмотрен в гл. 7, § 2. *. Преобразованиями подобия называются преобразования вида у = ах. Если в > 0, то преобразование подобия называется положительным. Шкалы разностей — это шкалы, которым соответствуют преобразования сдвига9. Ясно, что такие преобразования образуют подсо-вокупность положительных линейных преобразований. Шкалы разностей получаются нз интервальных шкал при фиксации единицы измерения. Для большинства социологических шкал трудно задать естественным образом такую единицу (исключение составляют шкалы типа «возраст», «стаж работы», «доход» и некоторые другие). Однако шкалу разностей можно получить, например, при отыскании шкальных значений рассматриваемых объектов с помощью некоторых методов парных сравнений (см. гл. 7).
СХЕМА 1. Соотношение типов шкал, используемых в социологии. Под незнанием типа шкал указывается соответствующий класс допустимых преобразований Сказанное подытожено в схеме 1, где указаны допустимые преобразования описанных шкал и отражено соотношение их типов. Признаки, аначения которых получены по порядковой или номинальной шкале, обычно называют качественными, а признаки, для получения значений которых использовалась шкала, тип которой ниже типа интервальной шкалы,— количественными. В соответствии с имеющейся традицией будем говорить, что дво шкалы позволяют достичь одного и того же уровня измерения, если эти шкалы являются шкалами одного типа (т. е. если соответствующие этим шкалам совокупности допустимых преобразований совпадают)". Адекватность математических методов. Одним из основных вопросов, встающих перед исследователем после осуществления изме-
16 Одному уровню измерений соответствуют и такие шкалы, как шкала отношений и шкала разностей, хотя они имеют разные совокупности допустимые преобразований. Однако для обоснования этого положения необходимо по 'кааать, что эти шкалы в определенном смысле подобны друг другу (об этом см.: Высоцкий В. С. О сравнении шкал.— В кн.: Прикладвой многомерный статистический анализ. М., 1978). •148 рения, является вопрос о том, какие математические методы он имеет право применять для анализа полученных чисел. Представляется целесообразным считать разрешенными (далее допустимыми, адекватными) только такие методы, результаты применения которых не зависят от того, по какой из возможных шкал получены исходные данные. Необходимым условием такой независимости является .инвариантность этих результатов относительно допустимых преобразований используемых шкал. Основанием для такого подхода служит то, что именно такие результаты в принципе поддаются содержательной интерпретации,, только они могут отражать реальные закономерности. Отметим, однако, что одной независимости результатов применения какого-либо метода от выбора конкретных используемых шкал отнюдь не достаточно для того, чтобы попытка их содержательной интерпретации увенчалась успехом. Необходимо также содержательное осмысление соответствующих результатов хотя бы для одной из возможных шкал. Подчеркнем, что понятие допустимости или недопустимости той или иной статистики (различных мер средней тенденции, мер разброса, коэффициентов связи между признаками и т. д.) является относительным. Все зависит от того, в каком «контексте» значения этой статистики используются, какие именно соотношения между этими значениями значимы для получения содержательных выводов. Так, сопоставление средних тенденций двух совокупностей может осуществляться с помощью сравнения средних арифметических зиа-чений некоторого признака по их величине, с помощью оценки разности (отношения) этих средних и т. д. И возможность использования средних арифметических значений зависит от того, какие именно соотношения между ними подлежат содержательной интерпретации. Подчеркнем следующее. Если удалось показать, что некоторое числовое соотношение можно содержательно проинтерпретировать, то не имеет значения, удастся ли при этом найти эмпирические аналоги отдельных входящих в это соотношение операций над числами. Например, можно делать содержательные выводы па основа сравнения по величине двух средних арифметических значений некоторого признака, никак не интерпретируя при этом суммы шкальных значений, вычисляемые в процессе нахождения средних арифметических. Как отмечалось выше, для проверки раэрешенности любого соотношения необходимо убедиться в том, что это соотношение и«ва-риантпо относительно допустимых преобразований использовавшейся при измерении шкалы (или нескольких шкал, если исходные данные получены по разным шкалам, но мы такой случай рассматривать не будем). Однако на практике такая проверка бывает довольно сложной. Соответствующая проблема в теории измерений называется проблемой адекватности рассматриваемого числового соотношения. Аналогично можно говорить о проблеме адекватности результатов применения какого-либо математического метода. Естественно, что чем уже круг допустимых преобразований:, тем: большее количество математических соотношений оставляют эта преобразования без изменения. Другими словами, чем выше тип шкалы, чем выше уровень измерения, тем большее количество математических методов можно применять к шкальным аначениям, получая при этом интерпретируемые результаты. Вопрос об адекватности используемых в социологии математических методов, как правило, является весьма сложным. Полученные к настоящей)' времени результаты касаются лишь небольшого числа методов. Рассмотрим некоторые из них. Прежде всего остановимся на вопросе о корректности исполь-аовапия различного рода средних и коэффициентов связи между признаками. Ясно, что любую статистику можно использовать в произвольном «контексте» только в том случае, если ее значение остается инвариантным относительно применения к исходным данным любого допустимого преобразования соответствующей шкалы. Нетрудно показать, что для номинальной шкалы, удовлетворяющей такому условию, средней будет мода, для порядковой шкалы — медиана и другие квантили. Значение среднего арифметического остается без изменения лишь для абсолютных шкал. Поэтому обращение с ним требует известной осторожности. Однако можно показать", что сравнивать по величине средние арифметические значения какого-либо признака можно уже в том случае, когда исходные данные получены по интервальной шкале (другими словами, результаты такого сравнения не изменяются при применении к исходным данным произвольного положительного линейного преобразования). Относительно коэффициентов связи можно сказать следующее. Инвариантными относительно допустимых преобразований рассматриваемых шкал являются значения коэффициентов связи, рекомендуемых в § 6 настоящей главы для соответствующего уровня измерения. Так, значение коэффициента корреляции г не изменяется при применении к исходным данным произвольного положительного линейного преобразования; значения коэффициентов Кендалла т и Спирмена г, инвариантны относительно произвольного монотонно возрастающего преобразования входящих в них величин; значения коэффициентов х*» Ф. ■?» -^> Т инвариантны относительно произволь< ного взаимно однозначного преобразования исходных данных ".
13 Подробно втот вопрос рассматривается в работе: Высоцкий В. С. Инвариантность коэффициентов связи.— В кв.: Математические методы и модели в социологии. М., 1977. 2. Группировка материала статистических наблюдений * Измеряя характеристики объекта, исследователь собирает первичный статистический материал. Дальнейшая его задача состоит в систематизации н обобщении результатов измерения для выявления характерных черт, существенных свойств тех или иных типов явлении, обнаружения закономерностей изучаемых процессов и проверки гипотез, лежащих в основе исследования. В основе исполь-ауемых методов обработки полученных материалов исследования лежит предварительное упорядочение первичных данных главным образом при помощи статистической группировки и составления статистических таблиц. Статистическая группировка. Распределение изучаемой совокупности на однородные группы по существенным для нее признакам •{характеристикам) называется статистической группировкой. Основное назначение группировки состоит, во-первых, в установлении численности каждой отдельно взятой части совокупности, расчлененной в соответствии со значениями определенного признака (или нескольких признаков), и, во-вторых, в изучении влияния причин и зависимости явлений. Главным вопросом метода группировки является правильный выбор группировочных признаков. Могут быть получены превосходные данные, но эти сведения пропадут совсем, если их группировка будет произведена неправильно. Поэтому при выборе признаков для отграничения явлений одного типа от явлений других типов необходимо руководствоваться не субъективными построениями, а содержательным анализом особенностей социальных явлений, задачами исследования, а также видом признаков, с которыми имеет дело исследователь. Основные группировки должны тщательно разрабатываться уже при составлении программы социологического исследования н с необходимостью отражать ключевые гипотезы. Ряды распределения. Результат группировки единиц наблюдения по какому-либо признаку называется статистическим рядом. Обозначим группировочнын признак х. Пусть это будет уровень образования каждого человека в данном списке лиц. Получим неупорядоченный ряд результатов отдельных наблюдений: 10, 5, 7, 8, 10, 10 10 (классы). Если отдельные наблюдения расположить в порядке возрастания указанных выше значений признака, то получим вариационный ряд: 5, 7, 8, 10, 10, 10, 10. По вариационному ряду количественного признака можно подсчитать, как часто каждое значение этого признака встречается п совокупности. В результате получим частотное распределение для данного признака. Иногда его называют эмпирическим или статистическим распределением. * Авторы выражают свою признательность Д. С. Шиерлингу за ряд полезных замечаний по статистической части зтой главы. Для вышеприведенного примера частотное распределение выглядит так: Отдельные значения признака (xt) 5 в 7 8 9 10 Частота (п{) 10 12 0 4 Объем совокупности (п всего человек) 8 Условимся каждое отдельное значение признака х обозначать х,, х2, xit .,., х„ (в данном примере это 5, 7, 8, 9 и 10 классов). Абсолютное число, показывающее, сколько раз встречается то или иное значение признака х, называется частотой и обозначается соответственно м„ пг, ns, ..., пк. Относительной частотой называется доля значений признака в общем числе наблюдений и обозначается тпи ..., тпк. Например, для приведенного частотного ряда частота наибольшего аначения признака (10 классов) равна 4, а относительная частота тпь = 4/8 = 0,5. Относительную частоту обычно выражают в процентах (/гаа = 50%). Сгруппированные данные. Как правило, для последующей статистической обработки или более наглядного представления данных отдельные значения признаков объединяются в группы (интервалы). В этом случае частоты соотносят уже не с каждым отдельным значением признака, как это делалось в предыдущем примере, а с рядом значений, попадающих в определенный интервал. Например, распределение уровня образования в вышеприведеп-пом примере может быть представлено в виде интервального ряда следующим образом: Образование (классы) 5—7 8 9—10 Частота 2 2 4 Частотное распределение с несгруппированными значениями иногда называют дискретным рядом распределения. При построении интервальных рядов большое значение имеет выбор типа, количества и размеров интервалов. Общее требование к этому выбору состоит в том, что группировка должна наиболее полно выявлять существенные свойства рядов распределения. Существующие формальные правила выбора оптимальной величины интервалов редко оказываются полезными при работе с социологическими данными". Как правило, приходится делать выбор Чежду двумя крайностями: слишком крупные интервалы для данного объема выборки скрадывают многие нюансы в описании явления, а слишком дробные ведут к статистически незначимым малым частотам гаутри интервала. Интервальные ряды распределения могут строиться о равными и неравными интервалами. Неравные интервалы применяются при неравномерном распределении частот значений группцровочного признака — для выделения качественно отличных типов явлений. Например, выбор интервалов при группировке данных распределе-
пия совокуппости опрошенных по возрасту можно основываться'па этапах жизнешюго цикла. При группировке семей по признаку «число книг в семье», опираясь на информацию ранее проведенных исследований о том, что чаще всего встречаются библиотеки с числом книг по 500 и реже — библиотеки, насчитывающие 10 000 книг, целесообразно установить неравные интервалы группировки, например такие: 1-50, 51-100, 101-200, 201-300, 301-500, 501—7Q0, 701-1000, 1001-2000, 2001-5000, 5001-10000. Если у исследователя нет предварительной информации о характере распределения по тому или иному признаку, то следует задавать равные интервалы. Равные интервалы также наиболее удобны при использовании методов математической статистики. Опыт показывает, что по каждому из признаков не следует брать более 20 группировочных интервалов. При образовании интервалов необходимо точно обозначить количественные границы группы, избегая таких обозначений границ интервалов, ври которых отдельные единицы совокупности могут быть отнесены в две соседние группы. Поэтому, как правило, необходимы дополнительные указания о том, считать ли граничные еначсния интервалов «включительно» или «исключительно». Довольно часто социологу приходится сталкиваться с ситуацией, когда необходимо провести перегруппировку материала, задав другие интервалы, но нет возможности при этом обратиться к первоначальным статистическим данным. При расщеплении интервала на несколько частей приходится вводить априорное предположение о частотном распределении внутри интервала, поскольку истинное распределение неизвестно. Самым простым является предположение о равномерности частотного распределения по отдельным значениям признака. Другие формы распределения требуют достаточно громоздких вычислений". Статистические таблицы. .Предусмотренные программой исследования и методиками обработки группировки объектов по каждому из признаков кладутся в основу статистических таблиц, обобщающих исходные данные. В дальнейшем составляют более сложные таблицы, позволяющие сопоставлять ряды распределений, и, наконец, комбинационные таблицы, в которых три или более признака перекрещиваются, комбинируются. По таким таблицам устанавливаются, измеряются и анализируются связи между признаками исследуемой совокупности объектов. Построение таблицы подчинено определенным правилам. Основное содержание таблицы должно быть отражено в названии (круг рассматриваемых вопросов, географические границы статистической совокупности, время, единицы измерения). Таблицы бывают простые, групповые и комбинационные. Простые таблицы представляют собой перечень, список, отдель-
«53 ньпс единиц совокупности сколичественной (или качественной) характеристикой каждой из них в отдельности. В групповых таблицах содержится группировка единиц совокупности по одному признаку, а в комбинационных — по двум п более признакам. Примером комбинационной разработки статистической таблицы может служить табл. 1.
Таблица 1. Распределение рабочей молодежи по возрастам прн поступлении па работу в Москве и Московской губернии в 20-е годы * По губернии Мотива Возраст, лет i------------------- юношей девушек юношей | девушек До 12 7,4 3,8 12,9 4,7 13—15 48,1 43,7 59,3 56,5 16-18 44,5 52,5 28,8 38,8 -100% 100% 100% 100% * Бликов Н. М. Социологическое исследование труда и воспитания молодежи 20-х годов.—* Социол. исслед., 1875, J* 1, с. 148.
Таким образом, метод группировки и представление материала в виде статистических таблиц уже дают определенные возможности для изучения социологических данных. С другой стороны, он является совершенно необходимым средством для дальнейшего анализа и применения более тонких статистических методов. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 * Взаимно однозначным называв! ся преобразование, с помощью которого различные числа переводятся в различные и одному и тому же числу соответствует только одно число.
* Взаимно однозначным называв! ся преобразование, с помощью которого различные числа переводятся в различные и одному и тому же числу соответствует только одно число. 5 Линейный преобразованием называется преобразование вида у = ах -J- Ь, Если а > О, то линейное преобразооаиие называется положительным,
5 Линейный преобразованием называется преобразование вида у = ах -J- Ь, Если а > О, то линейное преобразооаиие называется положительным,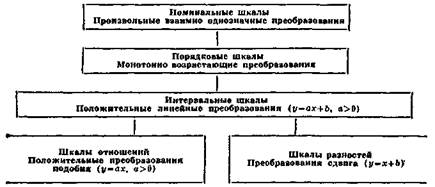
 • Преобразованием сдвига называется преобразование вида у = х -f- Ь, гдо Ь — произвольное действительное число.
• Преобразованием сдвига называется преобразование вида у = х -f- Ь, гдо Ь — произвольное действительное число. 11 См.: Орлов А. И. Устойчивость в социально-экономических моделях. М., 1979. В этой работе рассматривается возможность сравнения равного рода средних для шкал различных типов. При этом анализируется более широкий круг средних и типов шкал, чем круг, рассмотренный нами.
11 См.: Орлов А. И. Устойчивость в социально-экономических моделях. М., 1979. В этой работе рассматривается возможность сравнения равного рода средних для шкал различных типов. При этом анализируется более широкий круг средних и типов шкал, чем круг, рассмотренный нами. " Об этом см.: Юзбашев М. М.Методы изучения динамика распределения, зависимостей. М.,1974, с. 23—24.
" Об этом см.: Юзбашев М. М.Методы изучения динамика распределения, зависимостей. М.,1974, с. 23—24. 14 См., например: Венецкий И. Г. Вариационные ряди и их характеристики. М., 1970.
14 См., например: Венецкий И. Г. Вариационные ряди и их характеристики. М., 1970. Такая таблица представляет собой печто гораздо большее, чел простой перечень данных, она является способом и вместе с тем результатом определенной организации данных. Хороню сконструированная таблица позволяет исследователю более четко представить и описать смысл и сущность изучаемого им социального явления.
Такая таблица представляет собой печто гораздо большее, чел простой перечень данных, она является способом и вместе с тем результатом определенной организации данных. Хороню сконструированная таблица позволяет исследователю более четко представить и описать смысл и сущность изучаемого им социального явления.