
|
|
ГЛАВА 8. ЭЛЕМЕНТЫ ТЕОРИИ ИГР N ЛИЦ
Бескоалиционные игры n лиц Определение: Бескоалиционной игрой n лиц в нормальной форме называется объект
где Определение: Ситуация
Если сложилась равновесная ситуация, то каждому игроку в отдельности невыгодно от неё отклоняться. Если в игре Теорема: Если функции выигрыша игроков непрерывно дифференцируемы и точка равновесия
Условие теоремы вытекает из условий экстремума, так как в точке равновесия каждая функция
Пример бескоалиционной игры n лиц Пример. “Модель рынка” Имеются n участников, которые могут производить некоторый однородный товар и продавать его на рынке. Потенциальные покупатели данного товара имеют все вместе сумму денег равную a. Если i-й участник производит и выставляет на рынке количество товара
Предполагается, что в результате на рынке складывается такая цена, что весь предлагаемый товар покупается. Это значит, что цена
На производство не накладывается никаких условий, кроме условия неотрицательности, т. е.
Решение. Пусть Для определения ситуаций равновесия, лежащих внутри прямого произведения пространств стратегий участников, необходимо найти частные производные по всем переменным
Преобразуем полученное уравнение:
Умножим каждую часть уравнения на
а затем разделим на константу a
Просуммировав n уравнений (4), получим с учетом
Преобразуем полученное уравнение (5)
т. е.
Следовательно,
Подставляя (6) в (4), получим
При условии
ситуация
ГЛАВА 9. БЕСКОНЕЧНЫЕ ИГРЫ Непрерывные игры Определение: Класс игр, в которых хотя бы один из игроков имеет бесконечное множество возможных стратегий, называется классом бесконечных игр. Определение: Непрерывными играми называются бесконечные игры, в которых функции выигрышей непрерывно зависят от стратегий, выбираемых игроками. Теорема: Если в непрерывной антагонистической игре функция выигрыша первого игрока непрерывна по всем переменным, то у игроков есть оптимальные смешанные стратегии.
Примеры бесконечных игр Приведем примеры бесконечных игр двух лиц трех видов – непрерывной игры на единичном квадрате, дуэли и дифференциальной игры поиска. Играми с выбором момента времени, или играми типа дуэли, называются игры, характеризующиеся моментом выбора хода и вероятностями получения выигрыша в зависимости от времени, прошедшего от начала игры до момента выбора. В дифференциальных играх допускается делать ходы непрерывно и связывать поведение игроков условиями, описываемыми дифференциальными уравнениями. Пример. “Борьба за рынки” Одна из конкурирующих фирм – игрок А – пытается вытеснить другую фирму, игрока В, с одного из двух рынков сбыта. Предположим, что общая сумма средств, выделенная на это игроком А, равна 1. Решение. Типичной стратегией игрока А является разделение выделенной суммы на две части: Будем считать, что если игрок А добился превосходства на одном из рынков (на другом превосходства автоматически добивается игрок В), то он вытесняет противника с этого рынка и получает выигрыш, пропорциональный избытку вложенных средств с коэффициентом, характеризующим важность рынка. Этот коэффициент равен
Тогда функция выигрыша игрока В
Пример. “Игра типа дуэли” Два дуэлянта, игроки А и В, начинают сходиться в момент времени Решение. Если игрок А произведет выстрел в момент времени
С другой стороны, если
При
Таким образом, функция выигрыша
и антагонистическая игра задана. В частности, если игроки стреляют без промаха,
Пример. “Дифференциальная игра поиска” Ищущий, игрок А, стремится обнаружить уклоняющегося, игрока В. Оба игрока перемещаются с постоянными скалярными скоростями a и b соответственно по плоскости внутри некоторой поисковой области W. В любой момент каждый из игроков управляет своим перемещением, задавая направление вектора скорости. Решение: Пусть
Игра поиска заканчивается в тот момент, когда игроки сблизятся на расстояние
В случае успешного обнаружения выигрыш игрока А считается равным 1. Построение решения в этой игре существенно зависит от характера и степени информированности игроков.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
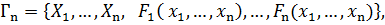
 – множество чистых стратегий i-го игрока,
– множество чистых стратегий i-го игрока,  ,
, 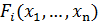 – функция выигрыша i-го игрока в ситуации
– функция выигрыша i-го игрока в ситуации  , сложившейся в результате выборов стратегий всеми игроками,
, сложившейся в результате выборов стратегий всеми игроками, 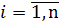 .
. – называется ситуацией равновесия в бескоалиционной игре
– называется ситуацией равновесия в бескоалиционной игре 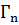 , если для каждого
, если для каждого  выполняется неравенство
выполняется неравенство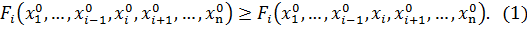
 , то необходимо выполнение условий
, то необходимо выполнение условий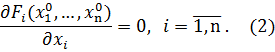
 достигает максимума по своей переменной
достигает максимума по своей переменной  при фиксированных остальных переменных. В общем случае необходимо учитывать возможную принадлежность равновесных стратегий
при фиксированных остальных переменных. В общем случае необходимо учитывать возможную принадлежность равновесных стратегий  границам множеств
границам множеств 
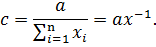
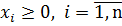 . Но производство связано с затратами. Возьмем простейший случай, когда затраты линейны, т. е. равны
. Но производство связано с затратами. Возьмем простейший случай, когда затраты линейны, т. е. равны  Следовательно, при таких условиях прибыль каждого участника будет определена следующим образом:
Следовательно, при таких условиях прибыль каждого участника будет определена следующим образом:
 . Получаем:
. Получаем: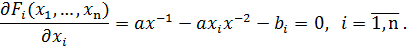
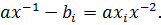
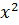
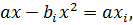
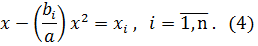
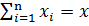 одно уравнение определяющее x:
одно уравнение определяющее x:
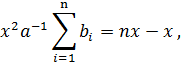
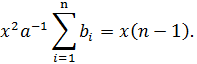


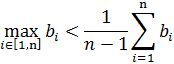
 будет равновесной. Это условие означает близость производственных затрат всех участников. Если же данное условие не выполняется, то некоторые участники могут “выбыть из игры”. Участникам выгодно произвести всем вместе очень мало товара, получив сумму a и практически не произведя затрат. Эту сумму можно распределить так, что все участники получат бóльшую прибыль, чем в точке равновесия. Однако такая ситуация не будет равновесной, т. е. каждому участнику в отдельности выгодно её нарушить. Чтобы подобные ситуации могли выступать в качестве решений, необходимо выйти за рамки бескоалиционных игр.
будет равновесной. Это условие означает близость производственных затрат всех участников. Если же данное условие не выполняется, то некоторые участники могут “выбыть из игры”. Участникам выгодно произвести всем вместе очень мало товара, получив сумму a и практически не произведя затрат. Эту сумму можно распределить так, что все участники получат бóльшую прибыль, чем в точке равновесия. Однако такая ситуация не будет равновесной, т. е. каждому участнику в отдельности выгодно её нарушить. Чтобы подобные ситуации могли выступать в качестве решений, необходимо выйти за рамки бескоалиционных игр. для первого рынка и
для первого рынка и  для второго. Подобным образом выглядят и стратегии игрока В: выделение им части
для второго. Подобным образом выглядят и стратегии игрока В: выделение им части  своей суммы на первый рынок и
своей суммы на первый рынок и  на второй.
на второй.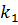 для первого рынка и
для первого рынка и  для второго. Тогда функция выигрыша
для второго. Тогда функция выигрыша  игрока А определяется формулой
игрока А определяется формулой

 У каждого пистолет заряжен одной пулей. Они встретятся в момент времени
У каждого пистолет заряжен одной пулей. Они встретятся в момент времени  , если только ни один из них не застрелит другого раньше. Каждый из дуэлянтов может выстрелить, когда пожелает. Если при этом одному из них удастся поразить противника, а самому остаться невредимым, то он становится победителем, его выигрыш равен 1 и дуэль тут же прекращается. Если оба промахнутся, дуэль закончится вничью, выигрыш каждого из игроков равен 0. Если оба выстрелят одновременно, и каждый поразит противника, то дуэль также считается окончившейся вничью.
, если только ни один из них не застрелит другого раньше. Каждый из дуэлянтов может выстрелить, когда пожелает. Если при этом одному из них удастся поразить противника, а самому остаться невредимым, то он становится победителем, его выигрыш равен 1 и дуэль тут же прекращается. Если оба промахнутся, дуэль закончится вничью, выигрыш каждого из игроков равен 0. Если оба выстрелят одновременно, и каждый поразит противника, то дуэль также считается окончившейся вничью. то его выстрел будет успешным с вероятностью
то его выстрел будет успешным с вероятностью  Подобным же образом выстрел игрока В в момент времени
Подобным же образом выстрел игрока В в момент времени  будет успешным с вероятностью
будет успешным с вероятностью  При условии
При условии 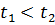 игрок А выигрывает с вероятностью
игрок А выигрывает с вероятностью  а проигрывает с вероятностью
а проигрывает с вероятностью  Его средний выигрыш при
Его средний выигрыш при 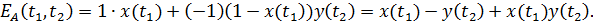
 его средний выигрыш будет равен
его средний выигрыш будет равен
 средний выигрыш
средний выигрыш
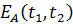 игрока А имеет вид
игрока А имеет вид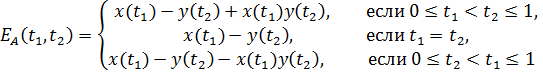
 тогда
тогда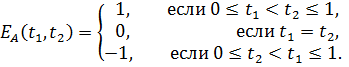
 – координаты игроков. Тогда имеем
– координаты игроков. Тогда имеем
 т. е. когда будет выполнено неравенство
т. е. когда будет выполнено неравенство