
|
|
ГЛАВА 5. БИМАТРИЧНЫЕ ИГРЫОпределение биматричных игр Предыдущие рассмотрения касались игр двух лиц с нулевой суммой, в которых интересы игроков были прямо противоположны, т. е. рассматривались матричные игры, а также позиционные игры, сводимые к матричным. Однако ситуации, в которых интересы игроков не обязательно являются противоположными, встречаются значительно чаще. Обобщением игр с нулевой суммой на случай непротивоположных интересов участников являются игры с ненулевой суммой. Рассмотрим конкретную ситуацию, в которой участвуют два игрока: игрок А – может выбрать любую из стратегий А1, … Аm, а игрок В – может выбрать любую из стратегий В1,…Вn. Запишем платежные матрицы для игроков А и В:
Если первый игрок выбрал свою i-ю стратегию, а второй – свою j-ю стратегию, то в результате такого совместного выбора первый игрок получает выигрыш Таким образом, в случае, когда интересы игроков различны, но необязательно противоположны, получаются две платежные матрицы: одна – матрица выплат игроку А, другая – матрица выплат игроку В. Поэтому подобные игры называются биматричными. Биматричная игра, как и матричная, происходит партиями. Цель каждого игрока – выиграть как можно большую сумму в результате большого числа партий. Понятия чистых и смешанных стратегий игроков в биматричных играх вводятся аналогично тому, как это было сделано в матричных играх. Если матричные игры являются играми со строгим соперничеством, поскольку выигрыш одного игрока в точности равен проигрышу другого, то в биматричных играх интересы игроков могут быть в большей или меньшей степени близки. В зависимости от того, запрещено или разрешено сотрудничество игроков, различают некооперативные и кооперативные игры.
Смешанные стратегии Так как интересы игроков не совпадают, нужно построить такое компромиссное решение, которое в одинаковой степени удовлетворяло бы обоих игроков. Иначе говоря, необходимо найти такую равновесную ситуацию, отклонение от которой уменьшает выигрыш каждого игрока. Следовательно, анализ биматричной некооперативной игры можно свести к поиску максиминных стратегий игроков, т. е. стратегий, которые обеспечивают игрокам получение максимально возможного гарантированного выигрыша вне зависимости от действий противника. Если два игрока А и В выбрали смешанные стратегии
Максиминные смешанные стратегии первого и второго игроков обеспечивают им гарантированные выигрыши
соответственно вне зависимости от поведения противника. В некооперативном случае игрокам имеет смысл придерживаться осторожных стратегий, т. е. максиминных.
5.3. Биматричные игры размера 2 Особое внимание уделим случаю, когда у каждого из игроков имеется ровно две стратегии, т. е. В биматричной игре размера 2
причём x1 + x2 = 1 y1 + y2 = 1 а средние выигрыши вычисляются по формулам: ЕА(X, Y) = а11х1у1 + а12х1 (1 – у1) + а21(1 – х1)у1 + а22(1 – х1)(1 – у1), ЕВ(X, Y) = b11х1у1 + b12х1 (1 – у1) + b21(1 – х1)у1 + b22(1 – х1)(1 – у1), или в более удобной форме
где Определение: Будем говорить, что пара чисел (Х*, У*) определяет равновесную ситуацию, если для любых x и у таких, что x
Выписанные неравенства (3) означают следующее: ситуация, определяемая смешанной стратегией Теорема 1 (точка равновесия по Нэшу): Всякая биматричная игра имеет хотя бы одну равновесную ситуацию в смешанных стратегиях. Теорема 2: Выполнение неравенств
равносильно выполнению следующих неравенств:
Другими словами, для того чтобы убедиться, что пара
только для двух чистых стратегий первого игрока А (
только для двух чистых стратегий второго игрока В ( Четыре неравенства (5) позволяют провести поиск точки равновесия уже вполне конструктивно. Отсюда вытекает условие следующей теоремы. Теорема 3: Для того чтобы в биматричной игре
пара
где D = b11 – b12 – b21 +b22, b= b22 – b21.
Пример 1. “Борьба за рынки” Небольшая фирма (игрок А) намерена сбыть партию товара на одном из двух рынков, контролируемых другой, более крупной фирмой (игрок В). Для этого фирма А готова сделать на одном из рынков соответствующие приготовления, например, развернуть рекламную кампанию. Господствующая на рынках фирма В может попытаться воспрепятствовать этому, приняв на одном из рынков предупредительные меры, в рамках закона. Не встречая противодействия на рынке, фирма А захватывает его; при наличии препятствий – терпит поражение. Будем считать для определенности, что проникновение фирмы А на первый рынок более выгодно для неё, чем на второй. Естественно также считать, что и борьба за первый рынок потребует вложения больших средств. Например, победа фирмы А на первом рынке принесет ей вдвое больший выигрыш, чем победа на втором, но зато и поражение при попытке освоиться на первом рынке полностью её разорит, а фирму В избавит от конкурента. Что же касается второго рынка, то при поражении фирмы А её потери будут не столь разорительны, но и победа принесёт не много. Как вести себя фирмам А и В? Решение. Для начала определим стратегии игроков. У фирмы А две стратегии: А1 – выбор первого рынка, А2 – выбор второго рынка. Такие же стратегии и у фирмы В: В1 – выбор первого рынка, В2 – выбор второго рынка. Для того чтобы составить платежные матрицы игроков, нужны расчетные количественные показатели, которые приведем в условных единицах: В1 В2 В1 В2
Если оба игрока выберут один и тот же рынок, то победа останется за более сильной фирмой В. То, что в ситуации Для нахождения равновесной ситуации используем теорему 3. Найдем необходимые величины C, D, a и b:
Подставляя полученные значения в неравенства (6) получаем:
Рассмотрим сначала неравенства (7):
Возможны следующие три случая:
Рассмотрим каждый из этих случаев подробно. 1) Полагая
Отсюда
2) Полагая
Значит,
3) Если
Решение полученной системы неравенств возможно лишь в случае когда
Аналогичным образом рассмотрим неравенства (8). Возможны три случая:
которые приводят к следующим результатам: 1) Если
2) Если
3) Если
Перенесем полученные результаты на чертеж. Введем на плоскости прямоугольную систему координат (x, y) и выделим на ней единичный квадрат, соответствующий неравенствам
Затем нанесем множество точек, которое описывается условиями 1), 2), 3) для x и y. Эти множества состоят из трех прямолинейных участков – двух лучей и одного отрезка – и представляют собой “зигзаги”. Нас будут интересовать только те части, которые попали внутрь единичного квадрата.
y
1
0 Общая точка построенных зигзагов – точка равновесия – имеет координаты
Значит, соответствующие смешанные стратегии игроков имеют следующий вид:
а средние выигрыши игроков равны:
Замечание: Разобьем рассмотренную биматричную игру на две матричные игры с нулевой суммой. 1. Игра с матрицей А.
Решая эту игру аналитическим методом, найдём оптимальные смешанные стратегии игроков и цену игры:
2. Игра с матрицей В.
Аналогичным образом, решая эту игру аналитическим методом, найдем оптимальные смешанные стратегии игроков и цену игры:
Сравнивая полученные результаты с решением биматричной игры, можно заметить следующее: если каждый игрок будет применять свои стратегии в этой игре исходя только из матрицы своих выигрышей, то его оптимальный средний выигрыш совпадает с его выигрышем при равновесной ситуации. Кроме того, по своей матрице игрок может найти и оптимальную смешанную стратегию другого игрока, но не свою. Пример 2. “Дилемма узников” Игроками являются два узника, находящиеся в предварительном заключении по подозрению в совершении преступления. При отсутствии прямых улик возможности их осуждения в большой степени зависят от того, заговорят они или будут молчать. Если оба будут молчать, то наказанием будет лишь срок предварительного заключения, и потери каждого из узников составят (-1). Если сознаются, то получат срок, учитывающий признание как смягчающее обстоятельство и потери каждого из узников составят в этом случае (-6). Если же заговорит только один из узников, а другой будет молчать, то в этом случае заговоривший будет выпущен на свободу и его потери равны 0, а сохраняющий молчание получит максимально возможное наказание и его потери составят (-9). Решение. Эта конфликтная ситуация приводит к биматричной игре, в которой каждый из игроков имеет по две стратегии – молчать или говорить. Матрицы выигрышей игроков А и В описываются следующим образом: М Г М Г
Проведем необходимые вычисления:
Отсюда
и тогда получаем, что 1. a) 2. a) Изобразим геометрически полученные результаты. y
3/2
0 1 3/2 x
Единственная равновесная ситуация – (0, 0). Это ситуация в которой каждый из игроков выбирает вторую чистую стратегию – сознаться – и его потери составляют 6, т. е.
Отклонение от ситуации равновесия одного из игроков не даёт ему никаких преимуществ. Однако при одновременном отклонении обоих каждый из них может получить больший выигрыш, чем в равновесной ситуации. Например, в ситуации (1, 1), когда оба игрока выбирают первую чистую стратегию – молчать, каждый из них теряет лишь 1. По условию задача является бескоалиционной, поэтому сговор между игроками недопустим. Значит при рассматриваемых обстоятельствах ситуация (1, 1) неустойчива – любой из узников, изменяя свою стратегию, увеличивает свой выигрыш, т. е. стремится избежать наказания. Пример 3. “Студент - преподаватель” Студент (игрок А) готовится к зачету, который принимает преподаватель (игрок В). Определите равновесную ситуацию. Решение. Можно считать, что у студента две стратегии: А1 – подготовиться к сдаче зачета и А2 – не подготовиться. У преподавателя также две стратегии: В1 – поставить зачёт и В2 – не поставить зачет. Таблица № 1. Выигрыш студента.
Таблица № 2. Выигрыш преподавателя.
Количественно это можно выразить, например, так:
Проведя необходимые вычисления:
получаем:
Отсюда следует, что 1. a) 2. a) Изобразим на графике полученные множества точек. y
1
1/2
0 1/5 1 x Данная игра имеет три точки равновесия, две из которых отвечают чистым стратегиям игроков: 1. 2. и одна – смешанной:
В данной задаче всё довольно ясно: наилучшим является выбор каждым из игроков первой чистой стратегии – хорошо подготовиться к зачету и поставить зачёт. В этой задаче реализуется весьма редкая возможность, когда функции выигрыша каждого из игроков достигают своих максимумов одновременно. Любое отклонение от ситуации (1, 1) одного из игроков или обоих игроков может привести только к уменьшению их выигрышей.
Некоторые итоги Из приведенных примеров видно, что числа C и D могут быть как положительными, так и отрицательными. Они могут, в частности, даже обращаться в нуль. Рассмотрим наиболее интересный случай, когда ни C ни D нулю не равны, т. е.
Тогда точка равновесия определяется парой
Эти формулы являются весьма примечательными: в равновесной ситуации выбор игрока А полностью определяется элементами платежной матрицы В,
и не зависит от элементов его собственной платежной матрицы, а выбор игрока В в равновесной ситуации полностью определяется элементами платежной матрицы игрока А,
и не зависит от элементов его собственной платежной матрицы. Значит равновесная ситуация обоих игроков определяется не столько стремлением увеличить собственный выигрыш, сколько желанием держать под контролем выигрыш другого игрока, т. е. минимизировать этот выигрыш. Отметим, что в биматричных играх, при наличии нескольких ситуаций равновесия, средний выигрыш игрока в разных равновесных ситуациях различен. В некоторых биматричных играх равновесные ситуации случаются и в чистых стратегиях. Не исключено существование равновесных ситуаций одновременно и в смешанных и в чистых стратегиях.
5.5. Примеры для самостоятельной работы 1. Найдите решения следующих биматричных игр:
2. “Семейный спор”. Семейная пара – муж и жена решают проблему: как им провести свой досуг. В городке, где они живут, имеется два вида развлечений: балет и футбол. У каждого из супругов есть свое любимое зрелище: жена предпочитает балет, а муж футбол. Однако супруги так привязаны друг к другу, что посещение любимого развлечения в одиночку доставляет им совсем не такое удовольствие, как присутствие на них вдвоем, т. е. если жена идет вечером на балет с мужем, она получает максимум удовольствия (4 ед.); муж недолюбливает балет, но присутствие на нем с женой скрашивает тягостное времяпровождение, муж получает 1 ед. удовольствия. История повторяется с точностью до наоборот, когда жена идет с мужем на футбол: муж получает 4 ед. удовольствия от игры любимой команды и присутствия любимой жены; жена получает 1ед. удовольствия, проведя вечер с мужем на футболе. В принципе муж может сходить на футбол, а жена – на балет в одиночку, но отсутствие супруга снижает удовольствие от любимых зрелищ – каждый из них получает по 2 ед. удовольствия. И наконец, вечер будет проведен совсем без пользы, если муж отправится на балет, в то время как жена будет на стадионе смотреть футбол, т. е. супруги получат по 0 ед. удовольствия. Определите равновесную ситуацию. 3.Две конкурирующие фирмы борются за право торговать на большей площади рынка. В зависимости от расширения площадей увеличивается и прибыль этих фирм. Как вести себя обеим фирмам, если они не могут договориться между собой, но хотят получать максимальную прибыль. Платежные матрицы заданы:
4. Два производителя продают на рынке один товар. Каждый из них может назначить цену товара: 400 руб. или 600 руб. Если оба производителя назначат цену 400 руб., то каждый из них получит чистую прибыль 12 млн. руб. Если оба производителя назначат цену 600 руб., то каждый из них получит чистую прибыль 16 млн. руб. Если же один назначит цену 400 руб., а другой – 600 руб., то тот производитель, который назначит меньшую цену, получит прибыль 20 млн. руб., а его конкурент – 4 млн. руб. Как должны выбирать свои стратегии игроки? 5. Две фирмы продают конкурирующие товары. Каждая из фирм должна решить, имеет ли смысл проводить рекламную кампанию. Если обе фирмы решат рекламировать свои товары, то первая фирма получит чистую прибыль в размере 10 млн. руб., а вторая – в размере 6 млн. руб. Если первая фирма будет рекламировать свой товар, а вторая не будет, то первая фирма получит прибыль 15 млн. руб., а прибыль второй окажется равной нулю. Если первая фирма не будет проводить рекламную кампанию, а вторая – будет, то прибыль первой фирмы составит 5 млн. руб., а прибыль второй – 8 млн. руб. Если же обе фирмы откажутся от проведения рекламной кампании, то первая фирма получит прибыль 10 млн. руб., а вторая – 2 млн. руб. Каковы оптимальные стратегии фирм?

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.
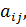 а второй – выигрыш
а второй – выигрыш 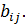 При этом не обязательно, чтобы
При этом не обязательно, чтобы 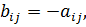 как в матричных играх.
как в матричных играх. и
и  соответственно, то математические ожидания выигрышей игроков равны:
соответственно, то математические ожидания выигрышей игроков равны: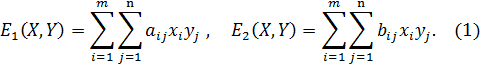

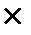 2. Ситуация равновесия
2. Ситуация равновесия .
.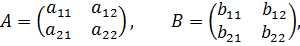
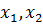 – вероятности выбора первым игроком А стратегий А1, А2,
– вероятности выбора первым игроком А стратегий А1, А2, – вероятности выбора вторым игроком В стратегий В1, В2,
– вероятности выбора вторым игроком В стратегий В1, В2, x2 = 1 - x1,
x2 = 1 - x1,



 ,
,  .
.
 , у
, у 
 выполняются одновременно следующие неравенства:
выполняются одновременно следующие неравенства: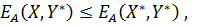
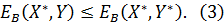
 , является равновесной, если отклонение от неё одного из игроков при условии, что другой сохраняет свой выбор, приводит к уменьшению выигрыша первого. Тем самым получается, что если равновесная ситуация существует, то отклонение от неё невыгодно самому игроку.
, является равновесной, если отклонение от неё одного из игроков при условии, что другой сохраняет свой выбор, приводит к уменьшению выигрыша первого. Тем самым получается, что если равновесная ситуация существует, то отклонение от неё невыгодно самому игроку.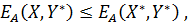
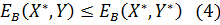
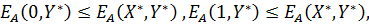
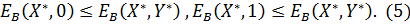
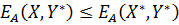
 ) и неравенства
) и неравенства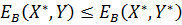
 ).
).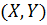 определяла равновесную ситуацию, необходимо и достаточно одновременное выполнение неравенств:
определяла равновесную ситуацию, необходимо и достаточно одновременное выполнение неравенств: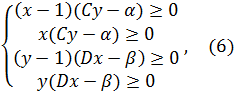

 выигрыш игрока В равен 5, а в ситуации
выигрыш игрока В равен 5, а в ситуации  – 1, подчеркивает, что первый рынок более выгоден (удобно расположен, хорошо посещаем и т. п.), чем второй. Выигрыш (-10) игрока А в ситуации
– 1, подчеркивает, что первый рынок более выгоден (удобно расположен, хорошо посещаем и т. п.), чем второй. Выигрыш (-10) игрока А в ситуации  и
и  , то здесь фирму А ждет настоящий выигрыш, больший на более выгодном рынке. Потери, которые при этом несёт фирма В, оказываются прямо противоположными.
, то здесь фирму А ждет настоящий выигрыш, больший на более выгодном рынке. Потери, которые при этом несёт фирма В, оказываются прямо противоположными.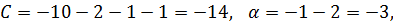
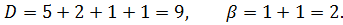

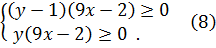

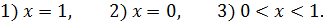
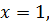 получаем
получаем

 получаем
получаем

 то
то


 тогда
тогда
 то
то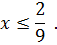
 то
то

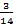 x
x 1
1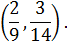
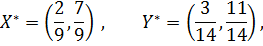


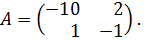
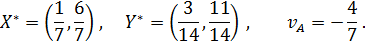

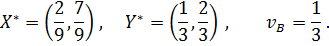

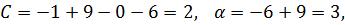

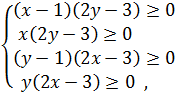
 b)
b)  c)
c) 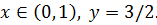
 b)
b)  c)
c) 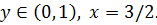

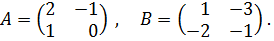
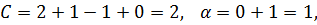
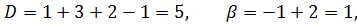
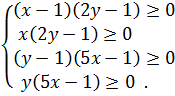
 b)
b)  c)
c) 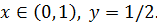
 b)
b)  c)
c) 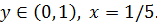

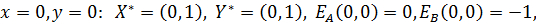
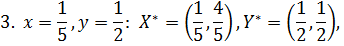

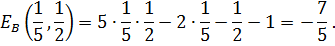
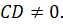
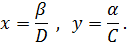
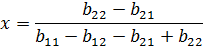
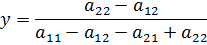
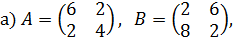
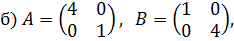
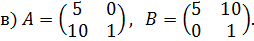
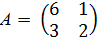 ,
, 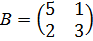 .
.