
|
|
Решение матричных игр с помощью задач линейногоПрограммирования Существует тесная связь между матричными играми и линейным программированием. Любая антагонистическая матричная игра размера Рассмотрим Определим интересы игрока А. Из следствия к теореме 3 следует, что при существующей чистой стратегии
Положим
тогда
Поскольку игрок A стремится сделать свой гарантированный выигрыш максимально возможным, то задача отыскания решения матричной игры сводится к следующей задаче: - найти неотрицательные величины
и такие, что их сумма минимальна
Рассмотрим теперь интересы игрока В. Аналогичным образом заключаем, что оптимальная смешанная стратегия
Обозначим
тогда
Поскольку игрок В стремится сделать свой гарантированный проигрыш минимально возможным, то задача отыскания решения матричной игры сводится к следующей задаче: - найти неотрицательные величины
и такие, что их сумма максимальна
Таким образом, чтобы найти решение данной игры необходимо составить пару двойственных задач и определить их решение. Исходя из всего полученного, сформулируем следующую теорему. Теорема 7 (о связи матричных игр с линейным программированием): Решение матричной игры с положительной платежной матрицей равносильно решению двойственных задач линейного программирования
При этом цена игры
а оптимальные значения
Следовательно, процесс нахождения решения матричной игры с использованием методов линейного программирования состоит из следующих этапов: 1. Если в исходной платежной матрице А есть отрицательные элементы или нули, то необходимо добавить ко всем элементам матрицы одно и то же достаточно большое положительное число C, так, чтобы все элементы матрицы 2. Составить пару двойственных задач линейного программирования, эквивалентных полученной матричной игре. 3. Определить оптимальные планы пары двойственных задач. 4. Используя соотношение между планами пары двойственных задач и оптимальными стратегиями и ценой игры, найти решение игры, заданной матрицей 5. Перейти к оптимальным смешанным стратегиям и цене игры с матрицей А, Замечание 1: Справедливо и обратное высказывание: для всякой симметричной пары двойственных задач можно записать матричную игру. Замечание 2: Каждая матричная игра имеет оптимальные стратегии, но не всякая задача линейного программирования имеет решение. Пример 1. Найти решение игры с платежной матрицей:
Решение. Поскольку Сведем данную матричную игру к паре взаимно двойственных задач линейного программирования согласно теореме 5:
при p1 ≥ 0, p2≥ 0, p3≥ 0. и
при q1 ≥ 0, q2 ≥ 0, q3 ≥ 0. Решаем обе задачи в двойственной симплекс-таблице. Таблица № 1.
Таблица № 2.
Таблица № 3.
Таблица № 4.
Из последней таблицы следует, что
Значит цена игры
а оптимальные стратегии игроков
Пример 2. Найти решение игры, определяемой матрицей:
Решение. Данная игра не имеет седловой точки, так как Для того чтобы перейти от заданной матричной игры к двойственным задачам линейного программирования необходимо к элементам исходной платежной матрицы добавить любое положительное число Тогда Следовательно, теперь можно составить пару двойственных задач:
при p1 ≥ 0, p2≥ 0. и
при q1 ≥ 0, q2 ≥ 0, q3 ≥ 0, q4 ≥ 0. Оптимальные решения полученных задач равны
Значит цена игры
а оптимальные стратегии игроков
2.3.5. Матричный метод решения игр размера В данном разделе рассмотрим игру, в которой число стратегий первого игрока А совпадают с количеством стратегий второго игрока В, т. е. игру с платежной матрицей Из следствия к теореме 5 следует, что для того чтобы пара смешанных стратегий X* и Y* была оптимальной и
Преобразуем данные неравенства в матричную форму:
где Y* - вектор-столбец, а X* - вектор-строка. Будем считать, что матричная игра допускает простое решение X*, Y*, если Теорема 8: Если игра с матрицей А допускает простое решение и матрица А невырождена, то
причем других простых решений не существует. Игра с матрицей А называется вполне смешанной, если у любой пары смешанных стратегий этой игры все координаты отличны от нуля. Следствие: Если игра с матрицей А вполне смешанная, а матрица А невырождена, то эта игра имеет единственную пару оптимальных смешанных стратегий:
Пример. Найти решение игры, определяемой матрицей
Решение. В заданной игре Найдем необходимые данные для определения оптимальных стратегий игроков и цены игры.
Таким образом, первый игрок А должен придерживаться стратегии при этом он получит доход не менее и его проигрыш не будет превосходить 4,356 ед.
Аффинное правило При поиске решения матричных игр часто оказывается полезным следующее свойство: Оптимальные стратегии у матричных игр, элементы матриц А и С которых связаны равенствами
где
Пример. Найти цену игры матрицы
если цена игра матрицы
равна 0. Решение. Элементы матриц А и С связаны равенством
Поэтому цена игры с матрицей С легко вычисляется:
Итерационный метод Опишем метод отыскания решения матричной игры – цены игры и оптимальных смешанных стратегий, в известной степени верно отражающий некоторую реальную ситуацию накопления опыта постепенной выработки игроками хороших стратегий в результате многих повторений конфликтных ситуаций. Основная идея этого метода заключается в том, чтобы мысленно, как бы смоделировать реальное практическое “обучение” игроков в ходе самой игры, когда каждый из них на опыте прощупывает способ поведения противника и старается отвечать на него наиболее выгодным для себя образом. Иными словами, всякий раз при возобновлении игры, игрок выбирает наиболее выгодную для себя стратегию, опираясь на предыдущий выбор противника. Проиллюстрируем этот метод на примере. Пример. Найти решение игры заданной матрицей:
Решение. Так как Опишем правила выбора ходов игроками, предположив для определенности, что начинает игрок А: ход игрока А – стратегия А1 – (2 0 3); игрок В выбирает свою стратегию так, чтобы выигрыш игрока А был минимален (отмечен выше полужирным шрифтом): ход игрока В – стратегия В2 – (0 3); игрок А выбирает свою стратегию так, чтобы его выигрыш при стратегии В2 игрока В был максимален: ход игрока А – стратегия А2 – (1 3 -3); игрок В выбирает свою стратегию так, чтобы “накопленный” выигрыш игрока А при стратегиях А1 и А2, (2 0 3) + (1 3 -3) = (3 3 0), был минимален: ход игрока В – стратегия В3 – (3 -3); игрок А выбирает свою стратегию так, чтобы его “накопленный” выигрыш при стратегиях В2 и В3 игрока В, (0 3) + (3 -3) = (3 0), был максимален: ход игрока А – стратегия А1 – (2 0 3); игрок В выбирает свою стратегию так, чтобы “накопленный” выигрыш игрока А при стратегиях А1, А2 и А1, (3 3 0) + (2 0 3) = (5 3 3), был минимален: ход игрока В – стратегия В2 – (0 3); и т. д. Разобьём последовательные ходы игроков А и В на пары и запишем результаты в таблице: Таблица № 1.
Введём некоторые пояснения к таблице № 1. 1-й столбец – номер n-го шага (пары последовательных ходов игроков А и В), 2-й столбец – номер i-ой стратегии, выбранной игроком А, 3-й столбец – “накопленный” суммарный выигрыш игрока А за первые n шагов при стратегии В1 игрока В, 4-й столбец – “накопленный” суммарный выигрыш игрока А за первые n шагов при стратегии В2 игрока В, 5-й столбец – “накопленный” суммарный выигрыш игрока А за первые n шагов при стратегии В3 игрока В (минимальный из этих выигрышей выделяется полужирным шрифтом), 6-й столбец – минимальный средний выигрыш игрока А, равный минимальному накопленному им выигрышу за первые n шагов, делённому на число этих шагов, 7-й столбец – номер k-ой стратегии, выбранной игроком В, 8-й столбец – “накопленный” суммарный выигрыш игрока А за первые n шагов при стратегии А1, 9-й столбец - “накопленный” суммарный выигрыш игрока А за первые n шагов при стратегии А2 (максимальный из этих выигрышей выделяется полужирным шрифтом), 10-й столбец – максимальный средний выигрыш игрока А, равный максимальному накопленному им выигрышу за первые n шагов, делённому на число этих шагов, 11-й столбец – среднее арифметическое минимального среднего выигрыша и максимального среднего выигрыша игрока А. Цена игры определяется приближённо по окончании любого из шагов. Например, за приближенную цену игры можно взять среднее арифметическое Смешанные стратегии противников определяются частотами появления чистых стратегий. Например, после 9-го шага имеем:
а после 10-го:
Сделаем несколько замечаний. Замечание 1: При увеличении числа шагов все три величины Замечание 2: Хотя сходимость итераций весьма медленна, тем не менее, даже такой небольшой расчет всегда даёт возможность находить ориентировочное значение цены игры и доли чистых сраегий. Замечание 3: Сравнительно медленную скорость сходимости можно объяснить целым рядом причин. Укажем одну из них, психологически наиболее интересную. Если, к примеру, игрок А уже нашёл оптимальную смешанную стратегию, то он не склонен останавливаться на ней – он продолжит попытки выиграть у противника В побольше, особенно если последний ещё не достиг оптимальной смешанной стратегии. Тем самым игрок А может невольно ухудшить своё положение. Замечание 4: Отметим два основных преимущества описанного метода: 1) итерационный метод прост и одновременно универсален, с его помощью легко можно найти приближённое решение любой матричной игры; 2) объём и сложность вычислений сравнительно слабо растут по мере увеличения числа стратегий игроков (размеров матрицы).

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 с конечными значениями m и
с конечными значениями m и  может быть сведена к решению пары двойственных задач линейного программирования специального вида.
может быть сведена к решению пары двойственных задач линейного программирования специального вида. игру с платежной матрицей
игру с платежной матрицей  , элементы которой все положительные. Для матрицы с отрицательными или нулевыми элементами игра может быть сведена к игре с положительной матрицей прибавлением достаточно большой константы к каждому элементу матрицы. Значит и цена игры – положительное число.
, элементы которой все положительные. Для матрицы с отрицательными или нулевыми элементами игра может быть сведена к игре с положительной матрицей прибавлением достаточно большой константы к каждому элементу матрицы. Значит и цена игры – положительное число.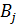 игрока В,
игрока В,  оптимальная смешанная стратегия
оптимальная смешанная стратегия  игрока A обеспечивает его средний выигрыш не меньший
игрока A обеспечивает его средний выигрыш не меньший 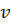 , т.е. выполняются соотношения:
, т.е. выполняются соотношения: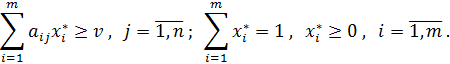
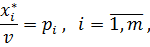
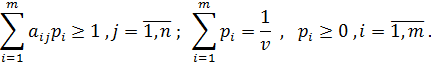
 удовлетворяющие неравенствам
удовлетворяющие неравенствам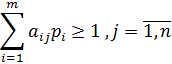

 игрока В при любой чистой стратегии
игрока В при любой чистой стратегии  игрока А,
игрока А,  обеспечивает его средний проигрыш, не большой
обеспечивает его средний проигрыш, не большой 
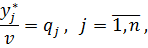
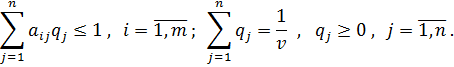
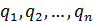 удовлетворяющие неравенствам
удовлетворяющие неравенствам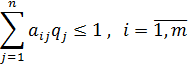

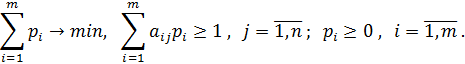
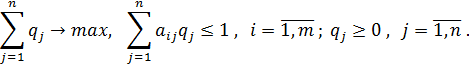

 связаны с оптимальными
связаны с оптимальными  равенством
равенством
 были положительными.
были положительными. .
. .
.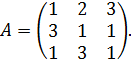
 , то данная игра не имеет седловой точки, а значит, и решения в чистых стратегиях нет. Цена игры лежит в диапазоне
, то данная игра не имеет седловой точки, а значит, и решения в чистых стратегиях нет. Цена игры лежит в диапазоне  . Решение игры следует искать в смешанных стратегиях.
. Решение игры следует искать в смешанных стратегиях.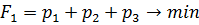
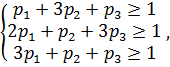
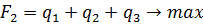
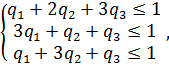




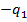
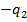

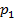







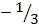
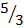
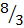

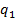
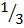

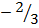







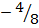




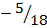






 ,
, 
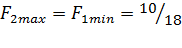 .
.

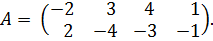
 , а значит, решение игры существует в смешанных стратегиях.
, а значит, решение игры существует в смешанных стратегиях.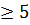 , например 5.
, например 5.
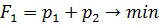
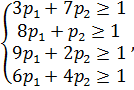
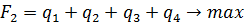
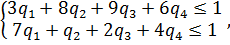
 ,
, 
 (проделать самостоятельно).
(проделать самостоятельно).
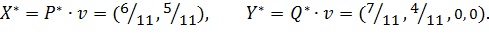


 при
при 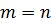 .
.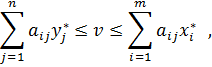
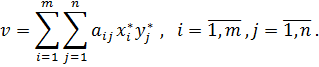
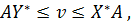
 где v – цена игры с платёжной матрицей A, It - единичная вектор-строка, I – единичный вектор-столбец. Тогда можно сформулировать следующую теорему:
где v – цена игры с платёжной матрицей A, It - единичная вектор-строка, I – единичный вектор-столбец. Тогда можно сформулировать следующую теорему: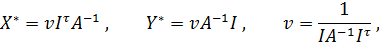


 , значит можно применить теорему и следствие к нашей задачи.
, значит можно применить теорему и следствие к нашей задачи.
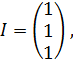
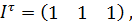

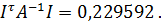
 ,
, , а второй игрок В – стратегии
, а второй игрок В – стратегии  ,
,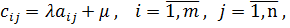
 произвольное, имеют одинаковые равновесные ситуации либо в чистых, либо в смешанных стратегиях, а их цены удовлетворяют следующему условию:
произвольное, имеют одинаковые равновесные ситуации либо в чистых, либо в смешанных стратегиях, а их цены удовлетворяют следующему условию:





 то
то  и игра не имеет седловой точки, значит, решение ищем в смешанных стратегиях.
и игра не имеет седловой точки, значит, решение ищем в смешанных стратегиях.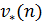


 , полученное на n-ом шаге.
, полученное на n-ом шаге.
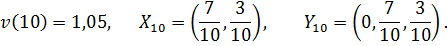
 будут приближаться к цене игры
будут приближаться к цене игры  но среднее арифметическое
но среднее арифметическое