
|
|
Решение матричных игр в чистых стратегиях. ПринципФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ “РИНХ” Н. А. Клитина ТЕОРИЯ ИГР Учебное пособие Ростов-на-Дону ОГЛАВЛЕНИЕ Глава 1. Предмет и содержание теории игр 1.1. Основные понятия и определения 1.2. Классификация игр Глава 2. Матричные игры. 2.1. Решение матричных игр в чистых стратегиях. Принцип минимакса 2.2. Смешанные стратегии 2.3. Методы решения матричных игр 2.3.1. Аналитический метод 2.3.2. Графический метод 2.3.3. Правило доминирования 2.3.4. Решение матричных игр с помощью задач линейного программирования 2.3.5. Матричный метод решения игр размера 2.3.6. Аффинное правило 2.3.7. Итерационный метод 2.4. Основные этапы поиска решения матричных игр 2.5. Примеры для самостоятельной работы Глава 3. Игры с “природой” 3.1. Основные понятия и критерии 3.2. Применение игр с “природой” в экономике 3.3. Примеры для самостоятельной работы Глава 4. Позиционные игры 4.1. Структура позиционной игры 4.2. Нормализация позиционной игры 4.3. Позиционные игры с полной информацией 4.4. Неантагонистические позиционные игры 4.5. Примеры для самостоятельной работы Глава 5. Биматричные игры 5.1. Определение биматричных игр 5.2. Смешанные стратегии 5.3. Биматричные игры размера 2 5.4. Некоторые итоги 5.5. Примеры для самостоятельной работы Глава 6. Оптимальность по Парето 6.1. Множество Парето 6.2. Метод идеальной точки 6.3. Оптимальность по Парето в биматричной игре 6.4. Примеры для самостоятельной работы Глава 7. Кооперативные игры 7.1. Переговорное множество 7.2. Точка решения Нэша 7.3. Примеры для самостоятельной работы Глава 8.Элементы теории игр n лиц 8.1.Бескоалиционные игры n лиц 8.2.Пример бескоалиционной игры n лиц Глава 9. Бесконечные игры 9.1. Непрерывные игры 9.2. Примеры бесконечных игр 9.3. Кооперативные непрерывные игры Библиографический список
ГЛАВА 1. ПРЕДМЕТ И СОДЕРЖАНИЕ ТЕОРИИ ИГР Основные понятия и определения В лекциях по теории оптимизации рассматривались такие задачи принятия решений, когда выбор решения осуществлялся одним лицом. В подобных задачах рационального ведения хозяйства решение выбирается при предположении о том, что известны целевая функция, различные способы действия и ограничения. Мы будем рассматривать задачи принятия решений в ситуациях с несколькими участниками, когда значение целевой функции для каждого из субъектов зависит и от решений, принимаемых всеми остальными участниками. Предметом теории игр являются такие ситуации, в которых важную роль играют конфликты и совместные действия. Определение: Игра - это действительный или формальный конфликт, в котором имеются, по крайней мере, два участника (игрока), каждый из которых стремится к достижению собственных целей. Определение: Раздел теории исследования операций, занимающийся математическими моделями принятия оптимальных решений в условиях конфликта, называется теорией игр. Определение: Ситуация называется конфликтной, если в ней участвуют стороны, интересы которых полностью или частично противоположны. Конфликт может возникнуть также из различия целей, которые отражают не только несовпадающие интересы различных сторон, но и многосторонние интересы одного и того же лица. Например, разработчик экономической политики обычно преследует разнообразные цели, согласуя противоречивые требования, предъявляемые к ситуации (рост объемов производства, повышение доходов и т.д.). Конфликт может проявляться не только в результате сознательных действий различных участников, но и как результат действия тех или иных "стихийных сил", т.е. "игр с природой". Множество подобных примеров можно встретить в социологии, военном деле, психологии, политологии и т.д. Также, примерами игр являются обычные игры: карточные, спортивные и другие. Именно с анализа подобных игр и начиналась математическая теория игр. Для того чтобы описать игру, необходимо задать её участников, которых принято называть игроками. Часто в игре не выделяют оперирующую сторону, а считают всех игроков равноправными и определяют оптимальные решения для всех участников. В некоторых играх игрокам имеет смысл объединяться и действовать совместно. Такие объединения называются коалициями действия. Для любой коалиции действия, в частности для каждого игрока, если он может действовать самостоятельно, должны быть определены её возможные действия, т.е. задано множество допустимых стратегий. Выбор игроками определённых стратегий определяет исход конфликта. Не все ситуации, складывающиеся при произвольном выборе стратегий, могут быть допустимыми. Недопустимые ситуации называются запрещёнными. Если имеются запрещённые ситуации, то не всякий выбор участниками стратегий определяет результат игры, и если некоторый выбор привел к запрещенной ситуации, то можно считать, что игра не состоялась или проведена не по правилам. Определение: Допустимые действия каждого из игроков, направленные на достижение некоторой цели, называются правилами игры. Определение: Однозначное описание выбора игрока в каждой из возможных ситуаций, при которой он должен сделать личный ход, называется стратегией игрока. Среди исходов игры одни являются более предпочтительными, а другие менее предпочтительными для участников, под которыми в данном случае можно понимать как отдельных игроков, так и их объединения – коалиции. Чтобы подчеркнуть, что эти объединения могут не совпадать с коалициями действий, будем называть их коалициями интересов. В большинстве рассматриваемых игр коалиции интересов либо совпадаю с коалициями действия, либо представляют собой отдельных игроков. Определение: Количественная оценка результатов игры называется функцией выигрыша или платежной функцией. Множество игроков или коалиций, пространства их стратегий, множества допустимых ситуаций и функции выигрыша полностью определяют заданную игру.
Классификация игр Различные виды игр можно классифицировать, основываясь на том или ином принципе: по числу игроков, по числу стратегий, по свойствам функций выигрыша, по возможности предварительных переговоров и взаимодействия между игроками в ходе игры. В зависимости от числа игроков различают игры с двумя, тремя и более участниками. В принципе, возможны также игры с бесконечным числом игроков. Определение: Игра называется парной, если в ней участвуют только две стороны. Согласно другому принципу классификации – по количеству стратегий – различают конечные и бесконечные игры. В конечных играх игроки располагают конечным числом возможных стратегий, и эти стратегии называют чистыми. Соответственно, в бесконечных играх игроки имеют бесконечное число возможных стратегий. Например, в ситуации «Продавец – Покупатель» каждый из участников может назвать любую устраивающую его цену и количество продаваемого (покупаемого) товара. Третий способ классификации игр – по свойствам функций выигрыша. Важным случаем в теории игр является ситуация когда выигрыш одного из игроков равен проигрышу другого, т.е. налицо прямой конфликт между игроками. Подобные парные называются играми с нулевой суммой или антагонистическими играми. Прямой противоположностью играм такого типа являются игры с постоянной разностью, в которых игроки и выигрывают, и проигрывают одновременно, так что им выгодно действовать сообща. Между этими крайними случаями имеется множество игр сненулевой суммой, где имеются и конфликты, и согласованные действия игроков. В зависимости от возможности предварительных переговоров между игроками различают кооперативные и некооперативные игры. Определение: Игра называется кооперативной, если до начала игры игроки образуют коалиции и принимают взаимообязывающие соглашения о своих стратегиях. Игра, в которой игроки не могут координировать свои действия подобным образом, называется некооперативной. Все антагонистические игры могут служить примером некооперативных игр. Примером кооперативной игры может служить ситуация образования коалиций в парламенте для принятия решения путем голосования, так или иначе затрагивающего интересы участников голосования. Если в игре образование коалиций вообще недопустимо, то такая игра называется бескоалиционной. Кроме того, игры можно классифицировать в соответствии с формой их задания. При этом различают позиционные игры и игры в нормальной форме. Большинство реальных игр представляют собой процесс, развернутый во времени, когда игроки делают в определенной последовательности свои ходы, обладая на каждом шаге определенной информированностью о предыдущих действиях других игроков, а выигрыши определяются только в конце игры. Такие игры называются позиционными. Примером такой игры являются шахматы. В позиционной игре стратегия игрока определяется правилами выбора на каждом шаге, т.е. представляет собой последовательность действий в зависимости от сложившейся в результате предыдущих ходов обстановки. Если же в игре стратегия представлена как одноактный выбор, то такая игра считается заданной в нормальной форме. ГЛАВА 2. МАТРИЧНЫЕ ИГРЫ
Решение матричных игр в чистых стратегиях. Принцип Минимакса Изучение игр начнем с простейшего случая антагонистической игры, которая называется матричной. Определение: Стратегия игрока называется оптимальной, если при многократном повторении игры она обеспечивает игроку максимально возможный средний выигрыш (или, что то же самое, минимально возможный проигрыш). Пусть имеются два игрока, один из которых может выбрать i-ю стратегию из m своих возможных стратегий (i=1,…,m), а второй, не зная выбора первого, выбирает j-ю стратегию из n своих возможных стратегий (j=1,…,n). В результате первый игрок выигрывает величину
Строки матрицы А соответствуют стратегиям первого игрока, а столбцы - стратегиям второго. Определение: Матрица А называется платежной матрицей. Определение: Игру, определяемую матрицей А, имеющей m строк и n столбцов, называют конечной игрой размерности m х n. Элемент
Величина Второй игрок при выборе некоторой стратегии j исходит из того, чтобы его проигрыш не превосходил максимального из значений j-го столбца матрицы (1), т.е. был меньше или равен
Величина Теорема 1: Нижняя цена игры всегда не превосходит верхней цены игры, т.е. При разумных действиях игроков фактический выигрыш первого игрока заключен между величинами Определение: Если выражения (2) и (3) равны между собой, т.е. Цена игры Седловая точка В случае если матрица игры имеет седловой элемент, то говорят, что игра имеет решение в чистых стратегиях. Теорема 2:
тогда и только тогда, когда существует седловая точка Пример 1. Две компании А и В продают два вида лекарств против гриппа. Компания А рекламирует продукцию на радио, телевидении и в газетах. Компания В, в дополнение к использованию радио, телевидения и газет, рассылает также по почте брошюры. В зависимости от умения и интенсивности проведения рекламной компании, каждая из компаний может привлечь на свою сторону часть клиентов конкурирующей компании. Приведенная ниже матрица характеризует процент клиентов, привлеченных или потерянных компанией А: B1 B2 B3 B4
Как вести себя компаниям? Решение. Компания А имеет три стратегии: A1 – реклама на радио, A2 – на телевидении, A3 – в газетах. У компании В на одну стратегию больше, так как добавляется рассылка брошюр по почте: В1, В2, В3, В4 соответственно. Решение игры основано на обеспечении наилучшего результата из наихудших для каждого игрока. Если компания А выбирает стратегию A1, то независимо от того, что предпримет компания В, наихудшим результатом является потеря компанией А 3% рынка клиентов в пользу компании В. Аналогично, при выборе стратегии А2 наихудшим исходом для компании А является увеличение рынка на 5% за счет компании В. И при выборе стратегии А3 наихудшим исходом является потеря 9% рынка в пользу компании В. Для того чтобы достичь наилучшего результата необходимо выбрать наибольший элемент из полученных, т. е. нижняя цена игры равна
Тогда вторая стратегия компании А, обеспечивающая получение данной нижней цены игры, называется максиминной. Для нахождения оптимальной стратегии компании В применим минимаксный принцип, т. е. в каждом столбце выбираем наихудший вариант для компании В, а затем из полученных элементов определяем наилучший исход игры для этой компании. Таким образом, найдем верхнюю цену игры:
В этом случае вторая стратегия компании В называется минимаксной. В данном примере верхняя цена игры совпадает с нижней ценой игры, значит, решение игры существует в чистых стратегиях и цена игры Пример 2. Найдите нижнюю цену игры, верхнюю цену игры, определите седловую точку, оптимальные чистые стратегии игроков и цену игры, если игра заданна следующей матрицей:
Решение. В каждой строке определим минимальный элемент, а в каждом столбце – максимальный:
max 8 9 4 8 Значит, нижняя цена игры равна:
Верхняя цена игры:
Следовательно,
Смешанные стратегии Рассмотрим вопрос о нахождении решения для игр, матрицы которых не содержат седлового элемента, т.е. нижняя и верхняя цены игры различны Применение минимаксной и максиминной стратегий для каждого из игроков обеспечивает выигрыш не меньше Определение: Стратегии, состоящие в случайном чередовании чистых стратегий, называются смешанными. Пусть смешанная стратегия первого игрока состоит в применении чистых стратегий i = 1,2,…,m с вероятностями
Тогда смешанные стратегии первого и второго игроков можно представить соответственно как
Функция Если первый игрок выбирает стратегию
Аналогично, с позиции второго игрока:
Цель игры можно теперь поставить в соответствие с задачей обеспечения игроками выигрыша, не меньшего Определение: Смешанные стратегии
для всех смешанных стратегий X и Y называются оптимальнымисмешанными стратегиями, а число Выписанные неравенства (9) означают следующее: левое неравенство - это отклонение первого игрока от оптимальной стратегии правое неравенство - это отклонение второго игрока от оптимальной стратегии Каждый игрок при многократном повторении игры, придерживаясь смешанных стратегий, получает более выгодный для себя результат. Оптимальное решение игры в смешанных стратегиях обладает следующим свойством: каждый игрок не заинтересован в отходе от своей оптимальной смешанной стратегии, если его противник применяет оптимальную смешанную стратегию, так как это ему не выгодно. Стратегии игроков в их оптимальных смешанных стратегиях называются активными. Теорема 3 (об активных стратегиях): Применение оптимальной смешанной стратегии обеспечивает игроку максимальный средний выигрыш (или минимальный средний проигрыш), равный цене игры Для оптимальных смешанных стратегий
Теорема фон Неймана (основная теорема матричных игр): Любая матричная игра имеет по крайне мере одно решение в области смешанных стратегий, а игроки имеют оптимальные смешанные стратегии, т.е.
В следующих двух теоремах формулируются необходимые и достаточные условия оптимальности стратегий. Теорема 4: Пусть
Аналогично, для того, чтобы
Введём обозначения:
Выражение (14) представляет собой выигрыш первого игрока при использовании им i-ой чистой стратегии, тогда как второй игрок применяет смешанную стратегию Y. Выражение (15) представляет собой выигрыш первого игрока при использовании им смешанной стратегии X, тогда как второй игрок применяет чистую j-ю стратегию. Следствие: Пусть
Аналогично, для того, чтобы
Теорема 5: Для того чтобы
Следствие: Для того чтобы
Теорема 6 (о свойствах оптимальных стратегий): Пусть если если Кроме того, имеют место равенства
Следствие:Если существует цена игры в чистых стратегиях, то она совпадает с ценой игры в смешанных стратегиях, которая всегда существует. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
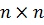
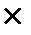 2. Ситуация равновесия
2. Ситуация равновесия , если
, если 
 , а второй проигрывает эту величину (если
, а второй проигрывает эту величину (если  , то второй игрок выигрывает у первого величину
, то второй игрок выигрывает у первого величину 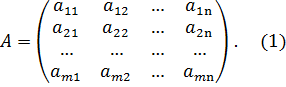
 . Поэтому первый игрок должен выбрать такую стратегию, чтобы максимизировать свой минимальный выигрыш
. Поэтому первый игрок должен выбрать такую стратегию, чтобы максимизировать свой минимальный выигрыш  :
: . (2)
. (2)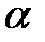 , определяемая формулой (2) называется нижней ценой игры, а стратегия
, определяемая формулой (2) называется нижней ценой игры, а стратегия  , обеспечивающая получение нижней цены, называется максиминной.
, обеспечивающая получение нижней цены, называется максиминной. . Второй игрок будет стремиться выбрать такую стратегию
. Второй игрок будет стремиться выбрать такую стратегию  , при которой его максимальный проигрыш
, при которой его максимальный проигрыш  был бы минимален, т.е. был бы равен:
был бы минимален, т.е. был бы равен: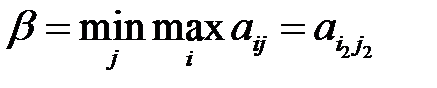 . (3)
. (3) , определяемая формулой (3), называется верхней ценой игры, а соответствующая верхней цене стратегия
, определяемая формулой (3), называется верхней ценой игры, а соответствующая верхней цене стратегия  .
. и
и  .
. (4), то величина
(4), то величина 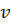 называется ценой игры.
называется ценой игры. , который минимален в строке
, который минимален в строке  и одновременно максимален в столбце
и одновременно максимален в столбце  . Элемент
. Элемент 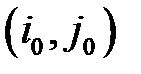 - седловой точкой, стратегия
- седловой точкой, стратегия  - максиминной стратегией для игрока А, стратегия
- максиминной стратегией для игрока А, стратегия 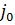 - минимаксной стратегией для игрока В, а сама игра - игра с седловой точкой.
- минимаксной стратегией для игрока В, а сама игра - игра с седловой точкой.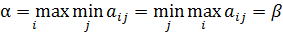
 .
.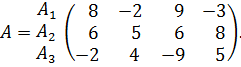

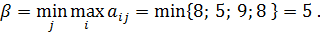
 . Выбор второй стратегии является оптимальным решением для компаний А и В при этом выигрыш будет в пользу компании А, так как её процент клиентов увеличится на 5%. Рассмотрим что может произойти при отклонении одной из компаний от выбранной оптимальной стратегии: например, если компания В перейдет к другой стратегии, то компания А может сохранить свой выбор стратегии А2, что приведёт к большей потере процентов клиентов для компании В. Седловая точка рассматриваемой игры равна (2, 2), где её координаты есть найденные оптимальные чистые стратегии игроков.
. Выбор второй стратегии является оптимальным решением для компаний А и В при этом выигрыш будет в пользу компании А, так как её процент клиентов увеличится на 5%. Рассмотрим что может произойти при отклонении одной из компаний от выбранной оптимальной стратегии: например, если компания В перейдет к другой стратегии, то компания А может сохранить свой выбор стратегии А2, что приведёт к большей потере процентов клиентов для компании В. Седловая точка рассматриваемой игры равна (2, 2), где её координаты есть найденные оптимальные чистые стратегии игроков.
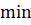


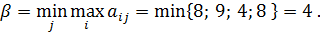
 , игра имеет решение в чистых стратегиях и существует седловая точка с координатами (2, 3). Оптимальной стратегией для первого игрока является вторая стратегия
, игра имеет решение в чистых стратегиях и существует седловая точка с координатами (2, 3). Оптимальной стратегией для первого игрока является вторая стратегия  , а для второго игрока В – третья стратегия
, а для второго игрока В – третья стратегия  . Первый игрок выиграл у второго 4 ед.
. Первый игрок выиграл у второго 4 ед. .
. и проигрыш не превышающий
и проигрыш не превышающий  Для каждого игрока естественно стремление увеличить выигрыш (уменьшить проигрыш). Поиски такого решения заключаются в том, что игроки применяют не одну, а несколько чистых стратегий, причем их выбор целесообразно осуществлять случайным образом.
Для каждого игрока естественно стремление увеличить выигрыш (уменьшить проигрыш). Поиски такого решения заключаются в том, что игроки применяют не одну, а несколько чистых стратегий, причем их выбор целесообразно осуществлять случайным образом. соответственно, а смешанная стратегия второго игрока - в применении чистых стратегий j = 1,2,…,n с вероятностями
соответственно, а смешанная стратегия второго игрока - в применении чистых стратегий j = 1,2,…,n с вероятностями  соответственно, причем
соответственно, причем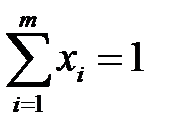 и
и  . (5)
. (5)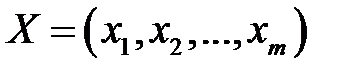 и
и 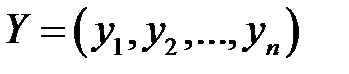 , для координат, которых выполняются условия (5). При этом чистые стратегии игроков могут пониматься как векторы
, для координат, которых выполняются условия (5). При этом чистые стратегии игроков могут пониматься как векторы  для i-ой чистой стратегии первого игрока и
для i-ой чистой стратегии первого игрока и 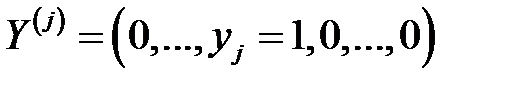 для j-ой чистой стратегии второго игрока. Если i-ая стратегия выбирается с вероятностью
для j-ой чистой стратегии второго игрока. Если i-ая стратегия выбирается с вероятностью  , а j-ая стратегия с вероятностью
, а j-ая стратегия с вероятностью  , то выигрыш
, то выигрыш  , т.е. математическое ожидание выигрыша первого игрока может быть определено по формуле:
, т.е. математическое ожидание выигрыша первого игрока может быть определено по формуле: . (6)
. (6) , определяемая выражением (6), называется платежной функцией.
, определяемая выражением (6), называется платежной функцией. , то он гарантирует себе выигрыш
, то он гарантирует себе выигрыш  , а потому может обеспечить и
, а потому может обеспечить и . (7)
. (7) . (8)
. (8) и проигрыша, не большего
и проигрыша, не большего  , соответственно.
, соответственно. и
и 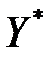 , для которых выполняются неравенства
, для которых выполняются неравенства (9)
(9) называется ценой игры для первого игрока. Совокупность оптимальных стратегий
называется ценой игры для первого игрока. Совокупность оптимальных стратегий  и цена игры
и цена игры 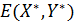 называется оптимальным решением игры.
называется оптимальным решением игры. . (10)
. (10) . (11)
. (11) – цена матричной игры. Для того чтобы
– цена матричной игры. Для того чтобы  ,
, 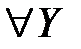 . (12)
. (12) ,
,  . (13)
. (13) , (14)
, (14)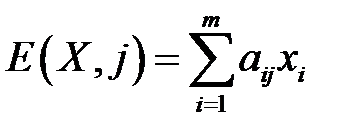 . (15)
. (15)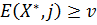 ,
,  .
.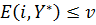 ,
,  .
.
 . (16)
. (16)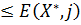 ,
, 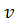 – цена игры. Тогда,
– цена игры. Тогда,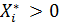 , то
, то  ,
,  , то
, то  ,
, 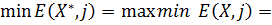

 .
.