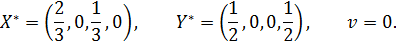|
|
Методы решения матричных игрАналитический метод Рассмотрим наиболее простой случай конечных игр размера
Требуется найти оптимальные смешанные стратегии игроков A и B Каковы бы ни были действия противника, выигрыш будет равен цене игры Для первого игрока составим систему уравнений:
Для второго игрока аналогично:
Если Решая системы уравнений, находим оптимальные решения
Пример. Дана платежная матрица
Найти решение. Решение. Так как для первого игрока – где для второго игрока – где Решая составленные системы уравнений, получаем:
Следовательно, оптимальные смешанные стратегии игроков имеют вид:
а цена игры
Это означает, что при выборе игроком А оптимальной смешанной стратегии
Графический метод Графический метод применим к играм, в которых хотя бы один игрок имеет только две стратегии. 1. Рассмотрим игру размера Пусть
Ожидаемый выигрыш первого игрока A при применении вторым игроком B первой стратегии составит
Аналогично найдём ожидаемые выигрыши первого игрока при применении вторым игроком 2, 3, …, Таблица № 1.
Следовательно, ожидаемый выигрыш первого игрока А, соответствующий чистой стратегии игрока В, вычисляется в виде:
Игрок А должен выбирать такие стратегии, чтобы максимизировать свой минимальный ожидаемый выигрыш, т. е.
На плоскости В результате описанной процедуры получается ломанная, которая и является графиком функции уравнения (3). Эта ломаная как бы огибает снизу все семейство построенных прямых и ее называют нижней огибающей этого семейства. Верхняя точка C построенной нижней огибающей определяет и цену игры, и оптимальную стратегию игрока А.
C
0 1 x1 Рис. 1 2. Рассмотрим игру размера Тогда платежная матрица имеет вид:
Аналогично предыдущему пункту предполагаем, что игра не имеет седловой точки. Решение такой игры находится для второго игрока В. Игрок В должен выбирать такие стратегии, чтобы минимизировать свой максимальный проигрыш, т. е.
Графиком функции
является верхняя огибающая семейства прямых, соответствующая чистым стратегиям первого игрока А. Нижняя точка D построенной верхней огибающей определяет цену игры и оптимальную стратегию игрока В.
0 1 y1 Рис. 2 Пример 1. Найти решение игры заданной матрицей:
Решение. Так как Пусть Таблица № 2.
Строим на координатной плоскости 6 (4) 4 (2) (1) 3 2 (3) 2 0 1 x1 Рис. 3 На пересечении прямых (3) и (4) нижней огибающей лежит её наивысшая точка. Решая систему уравнений
получаем
Значит, оптимальная стратегия первого игрока А и его цена игры соответственно равны:
Теперь найдем оптимальное решение второго игрока. Пусть Таблица № 3.
Изобразим на плоскости
0 1 y3 Рис. 4 Решая систему уравнений:
получаем
Следовательно, оптимальное решение второго игрока:
Полное решение игры будет иметь следующий вид:
Пример 2. Найти решение игры заданной платежной матрицей:
Решение. Игра не имеет седловой точки, так как Пусть Таблица № 4.
Построим на координатной плоскости 6 (4)
4 (1) 3 (2) 3 2 (3) 2
0 1 y1 Рис. 5 На верхней огибающей в точке пересечения прямых (1) и (3) расположено минимальное значение цены игры. Решая систему уравнений этих прямых
получаем
Значит, оптимальная стратегия второго игрока В и его цена игры соответственно равны:
Пусть Таблица № 5.
Изобразим на плоскости
2 2
0 1 x1 Рис. 6 Решая систему уравнений:
получаем
Следовательно, оптимальное решение первого игрока:
Полное решение игры будет иметь следующий вид:
Правило доминирования В целом ряде случаев анализ платежной матрицы обнаруживает, что некоторые чистые стратегии не могут внести никакого вклада в исходные оптимальные смешанные стратегии. Отбрасывание подобных стратегий позволяет заменить первоначальную матрицу на матрицу выигрышей меньших размеров. Рассмотрим игру размера
Определение: Будем считать, что j-я стратегия матрицы А
Если в матрице А одна из строк (j) доминируют другую (i), то число строк можно уменьшить путем отбрасывания доминируемой строки (i). Определение: Будем считать, что l-й столбец матрицы А
доминирует k-й столбец этой матрицы
если одновременно выполняются следующие неравенства:
Если в матрице А один из столбцов (l-й) доминирует другой столбец (k-й), то число столбцов в матрице А можно уменьшать путем отбрасывания доминируемого столбца (k). Замечание 1: Игрок А (игрок В) поступит разумно, если будет избегать стратегий, которым в матрице игры отвечают доминируемые строки (столбцы). Замечание 2: Оптимальные смешанные стратегии в игре с матрицей, полученной усечением исходной за счет доминируемых строк и столбцов, дадут оптимальное решение в исходной игре: доминируемые чистые стратегии игроков в смешении не участвуют, поэтому соответствующие им вероятности равны нулю. Замечание 3: При отбрасывании доминируемых строк и столбцов некоторые из оптимальных стратегий могут быть потеряны. Однако цена игры не изменится, и по усечённой матрице может быть найдена хотя бы одна пара оптимальных смешанных стратегий. Пример. Рассмотрим игру с матрицей
Решение. Применим правило доминирования. Сравнивая строки матрицы, видим, что 1-я строка совпадает с 4-й строкой, или что то же, стратегия А4 дублирует стратегию А1. Значит одну из этих строк можно вычеркнуть, не нанося ущерба решению:
Сравнивая поэлементно 1-ю и 2-ю строки, замечаем, что все элементы 1-й строки больше либо равны соответствующим элементам 2-й строки, значит 1-я строка доминирует 2-ю строку, или, что то же, стратегия А1 доминирует стратегию А2. Это позволяет уменьшить число строк матрицы, т. е. можно вычеркнуть доминируемую сроку А2:
Перейдем к рассмотрению столбцов. Замечая, что элементы 4-го столбца полученной матрицы меньше соответствующих элементов 3-го столбца, т. е. 4-й столбец доминирует 3-й столбец, приходим к игре размера
Продолжить уменьшение матрицы нельзя, так как доминируемых столбцов больше нет. Для нахождения оптимального решения полученной игры применим графический способ. Тогда оптимальные смешанные стратегии игроков А и В и цена игры равны следующим значениям:
Возвращаясь к исходной игре размера

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 без седловой точки с платежной матрицей:
без седловой точки с платежной матрицей:
 и цену игры
и цену игры 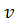 .
.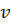 . Это означает, что если первый игрок A придерживается своей оптимальной стратегии
. Это означает, что если первый игрок A придерживается своей оптимальной стратегии  , то второму игроку B не имеет смысла отступать от своей оптимальной стратегии
, то второму игроку B не имеет смысла отступать от своей оптимальной стратегии  В игре
В игре 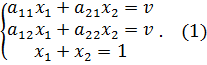
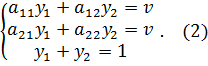
 и игроки имеют только смешанные оптимальные стратегии, то определитель матрицы отличен от нуля, следовательно, полученные системы уравнений имеют единственное решение.
и игроки имеют только смешанные оптимальные стратегии, то определитель матрицы отличен от нуля, следовательно, полученные системы уравнений имеют единственное решение. и цену игры
и цену игры 

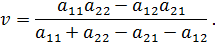
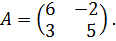
 то
то  и игра не имеет седловой точки, значит, решение ищем в смешанных стратегиях, цена игры находится между
и игра не имеет седловой точки, значит, решение ищем в смешанных стратегиях, цена игры находится между  т. е.
т. е.  Составим системы уравнений для каждого из игроков:
Составим системы уравнений для каждого из игроков: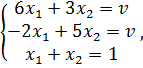
 вероятность выбора первым игроком первой стратегии,
вероятность выбора первым игроком первой стратегии,  вероятность выбора первым игроком второй стратегии;
вероятность выбора первым игроком второй стратегии;
 вероятность выбора вторым игроком первой стратегии,
вероятность выбора вторым игроком первой стратегии,  вероятность выбора вторым игроком второй стратегии.
вероятность выбора вторым игроком второй стратегии.
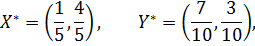
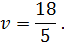
 против оптимальной смешанной стратегии
против оптимальной смешанной стратегии  игрока В, игрок А получит средний выигрыш 18/5 ден. ед., а игрок В – средний проигрыш 18/5 ден. ед.
игрока В, игрок А получит средний выигрыш 18/5 ден. ед., а игрок В – средний проигрыш 18/5 ден. ед. .
. – платежная матрица. Предполагаем, что игра не имеет седловой точки, значит, решение будем искать в смешанных стратегиях. Первый игрок А применяет первую стратегию с вероятностью
– платежная матрица. Предполагаем, что игра не имеет седловой точки, значит, решение будем искать в смешанных стратегиях. Первый игрок А применяет первую стратегию с вероятностью  вторую стратегию с вероятностью
вторую стратегию с вероятностью 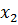 , причём
, причём  т. е.
т. е. 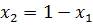 . Второй игрок В применяет первую стратегию с вероятностью
. Второй игрок В применяет первую стратегию с вероятностью 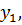 вторую стратегию с вероятностью
вторую стратегию с вероятностью  и т. д.,
и т. д., 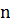 - ую стратегию с вероятностью
- ую стратегию с вероятностью  , причём
, причём
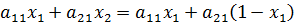
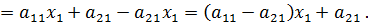



 (3)
(3)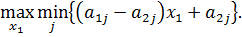
 уравнение (3) описывает прямую. Тем самым, каждой чистой стратегии игрока В на этой плоскости соответствует своя прямая. Для начала на плоскости (x1,
уравнение (3) описывает прямую. Тем самым, каждой чистой стратегии игрока В на этой плоскости соответствует своя прямая. Для начала на плоскости (x1,  , путем визуального сравнения соответствующих ему значений
, путем визуального сравнения соответствующих ему значений  .
.
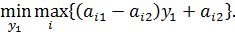
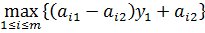

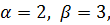 то
то 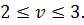 Определим ожидаемые выигрыши игрока А при применении игроком В соответствующей чистой стратегии.
Определим ожидаемые выигрыши игрока А при применении игроком В соответствующей чистой стратегии. – вероятность выбора первым игроком стратегии А1, тогда
– вероятность выбора первым игроком стратегии А1, тогда 
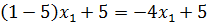
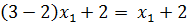

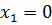 и точке пересечения с вертикальной прямой
и точке пересечения с вертикальной прямой  Затем находим нижнюю огибающую для построенных прямых.
Затем находим нижнюю огибающую для построенных прямых.
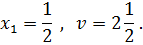
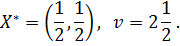
 – вероятности выбора вторым игроком стратегий В1, В2, В3, В4 соответственно. Выделяем из четырех чистых стратегий игрока В стратегии В3 и В4, которые соответствуют прямым (3) и (4), определяющим наивысшую точку нижней огибающей, тогда стратегии В1, В2 вторым игроком не выбираются, поэтому
– вероятности выбора вторым игроком стратегий В1, В2, В3, В4 соответственно. Выделяем из четырех чистых стратегий игрока В стратегии В3 и В4, которые соответствуют прямым (3) и (4), определяющим наивысшую точку нижней огибающей, тогда стратегии В1, В2 вторым игроком не выбираются, поэтому  Найдем ожидаемые проигрыши второго игрока при применении игроком А первой и второй чистых стратегий.
Найдем ожидаемые проигрыши второго игрока при применении игроком А первой и второй чистых стратегий.
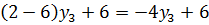
 полученные прямые, определим верхнюю огибающую этих прямых и минимальное значение цены игры на ней.
полученные прямые, определим верхнюю огибающую этих прямых и минимальное значение цены игры на ней. 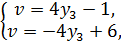
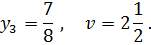

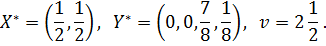

 значит, решение существует только в смешанных стратегиях. Платежная матрица имеет размер
значит, решение существует только в смешанных стратегиях. Платежная матрица имеет размер  поэтому, вначале будем искать оптимальное решение для второго игрока. Определим ожидаемые проигрыши игрока В при применении игроком А соответствующей чистой стратегии.
поэтому, вначале будем искать оптимальное решение для второго игрока. Определим ожидаемые проигрыши игрока В при применении игроком А соответствующей чистой стратегии. – вероятность выбора вторым игроком стратегии В1, тогда
– вероятность выбора вторым игроком стратегии В1, тогда  – вероятность выбора вторым игроком стратегии В2.
– вероятность выбора вторым игроком стратегии В2.

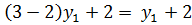

 полученные прямые и найдем их верхнюю огибающую.
полученные прямые и найдем их верхнюю огибающую.
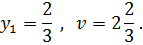
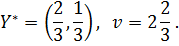
 – вероятности выбора первым игроком стратегий А1, А2, А3, А4 соответственно. Прямые, пересекающиеся в минимаксной точке, соответствуют первой и третьей чистым стратегиям первого игрока, тогда стратегии А2 и А4 первый игрок не выбирает, это означает, что
– вероятности выбора первым игроком стратегий А1, А2, А3, А4 соответственно. Прямые, пересекающиеся в минимаксной точке, соответствуют первой и третьей чистым стратегиям первого игрока, тогда стратегии А2 и А4 первый игрок не выбирает, это означает, что  Следовательно,
Следовательно,  Найдем ожидаемые выигрыши первого игрока.
Найдем ожидаемые выигрыши первого игрока.

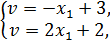
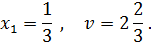
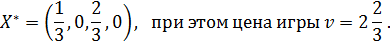

 с платежной матрицей:
с платежной матрицей: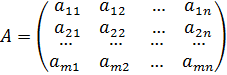 .
. доминирует i-ю стратегию этой матрицы
доминирует i-ю стратегию этой матрицы  , если одновременно выполняются следующие n неравенств:
, если одновременно выполняются следующие n неравенств: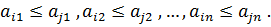
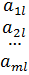

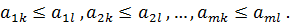
 .
. значит
значит  и игра не имеет седловой точки, а цена игры находится в пределах отрезка
и игра не имеет седловой точки, а цена игры находится в пределах отрезка 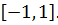

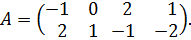
 с помощью вычеркивания 3-го столбца:
с помощью вычеркивания 3-го столбца: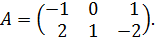
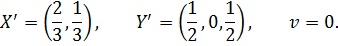
 , получаем окончательный ответ:
, получаем окончательный ответ: