
|
|
Позиционные игры с полной информациейПозиционная игра называется игрой с полной информацией, если в каждой позиции любой её партии игрок, делающий ход знает, какие альтернативы были выбраны на предыдущих ходах. Основная особенность позиционной игры с полной информацией состоит в том, что соответствующая ей матрица выигрышей всегда имеет седловую точку, т. е. в игре существуют оптимальные чистые стратегии, и, значит, равновесная ситуация. Теорема 1: Любая позиционная игра с полной информацией эквивалентна некоторой матричной игре, решение которой существует в чистых стратегиях. Пример 1. “Выкладывание монет на стол”. Два игрока поочерёдно кладут монеты одинаковых размеров на обыкновенный стол, всякий раз выбирая произвольное доступное место для монеты (взаимное накрывание монет не допускается). Тот из игроков, кто положит монету, не оставляющую места для новых монет, выигрывает. Решение. Эта игра с полной информацией. Существует вполне определенная стратегия, обеспечивающая выигрыш тому из игроков, кто начинает игру. А именно, начинающий игру должен положить первую монету точно в центр стола и на каждый ход противника отвечать симметричным ходом. Исход игры от стратегий второго игрока не зависит. Пример 2. “Переговоры”. В переговорах участвуют две стороны: А и В. Сначала сторона А высказывает одно из нескольких предположений, способных заинтересовать сторону В. Затем сторона В, ознакомившись с предложением стороны А, высказывает одно из нескольких встречных предложений, способных, по её мнению, заинтересовать сторону А. В свою очередь, сторона А, ознакомившись с реакцией стороны В на сделанные предложения, высказывает ей новое предложение, внеся одну из нескольких возможных корректировок в свое первоначальное предложение с учетом мнения стороны В, и т. д. Если предмет переговоров сложен, то подобный обмен ходами может затянуться. Однако любые переговоры непременно заканчиваются, и на финише ждет функция выигрышей. Решение. Смоделируем короткий переговорный процесс трехходовой позиционной игрой. Предположим, что переговоры заканчиваются через три хода, на каждом из которых соответствующая сторона имеет возможность выбора из двух альтернатив, и опишем соответствующую позиционную игру. 1-й ход делает сторона А: она выбирает одно из двух возможных предложений – число x из множества двух чисел 2-й ход делает сторона В: она выбирает число y из множества двух чисел 3-й ход делает сторона А: она выбирает число z из множества двух чисел После этого сторона А либо получает вознаграждение (например, в виде кредита от стороны В), либо выплачивает стороне В штраф. Все эти возможности описываются функцией выигрышей
Изобразим графически данную игру:
Рис. 3. Позиционная игра с полной информацией, состоящая из 3-х ходов. Описанная позиционная игра является игрой с полной информацией. Поскольку игрок В знает выбор игрока А на первом ходе, то у него существует четыре стратегии: Игрок А знает выбор игрока В и свой собственный, значит существует восемь стратегий. Пусть стратегии игрока Например, выбор игроком А стратегии Составим таблицу выигрышей для игрока А: Таблица № 6.
Перейдем от таблицы к соответствующей матрице
Вследствие того, что рассматриваемая позиционная игра является игрой с полной информацией, полученная матрица всегда имеет решение в чистых стратегиях при любой функции выигрышей.
Замечание 1: Графическое представление и функция выигрышей полностью определяет позиционную игру. При построении информационных множеств необходимо соблюдать два правила: 1) в одно информационное множество могут входить позиции только одного игрока, 2) цепь, определяющая партию игры, может иметь с информационным множеством не более одной общей позиции. Замечание 2: В рассмотренных примерах основное внимание было уделено описанию процесса нормализации позиционной игры. Следующий шаг – отыскание цены игры и оптимальных стратегий игроков – проводится методами, о которых рассказывается в главе “Матричные игры”. 4.4. Неантагонистические позиционные игры Ранее достаточно подробно рассматривались позиционные игры двух лиц, где были явно выражены интересы одного из игроков, игрока А. Следует, однако, иметь в виду, что в одних случаях интересы игрока В могут быть полностью противоположными интересам игрока А, в то время как в других вполне может оказаться, что то, что хорошо для одного игрока, необязательно плохо для другого. Приведём два простых примера. Пример 1. Рассмотрим позиционную игру, состоящую из двух ходов, которые последовательно делают участвующие в ней игроки А и В. Первый ход делает игрок А, второй – игрок В, зная о выборе игрока А. Функции выплат игрокам А и В –
Максимизируйте выигрыши для обоих игроков. Решение. Определим ходы игроков и построим дерево рассматриваемой игры. 1-ый ход делает игрок А: выбирает один из двух возможных вариантов – число x из множества чисел 2-ой ход делает игрок В: выбирает число y из множества Дерево игры имеет вид:
Исход игры зависит от того, каковы намерения игрока В – максимизировать свой выигрыш:
или максимизировать свой относительный выигрыш:
В первом случае это достигается так:
Во втором случае:
Пример 2. Игра задается деревом событий:
Решение. 1-ый ход делает игрок А: выбирает один из двух возможных вариантов – число x из множества чисел Если Если При В случае когда каждый из игроков стремится к получению максимального выигрыша и любые виды кооперации запрещены, исход игры ясен – игрок А выбирает 4.5. Примеры для самостоятельной работы 1. Функции выплат игроку А за счет игрока В задаются следующим образом:
Найдите оптимальные стратегии игроков и цену игры, если а) первый ход делает игрок А, второй – игрок В, не зная о выборе игрока А; б) первый ход делает игрок А, второй – игрок В, зная о выборе игрока А. 2. Дайте графическое представление, приведите к нормальной форме позиционную игру с функцией выигрышей W(x,y,z):
Найдите оптимальные стратегии игроков и цену их игры, если а) первый ход делает игрок А, второй – игрок В, не зная о выборе игрока А. Третий ход делает игрок А, зная выбор игрока В, но не помня собственного выбора на 1-ом ходе; б) первый ход делает игрок А, второй – игрок В, зная о выборе игрока А. Третий ход делает игрок А, не зная выбора игрока В, но помня собственный ход; в) первый ход производится случайным образом с вероятностями 0,3 при выборе 1 альтернативы и 0,7 при выборе 2 альтернативы. Второй ход делает игрок А, зная результат случайного выбора. Третий ход делает игрок В, не зная результат случайного выбора на первом ходе, но зная выбор игрока А на втором ходе. 3. Два участника играют в некоторую игру. Первый ход делает игрок А, второй – игрок В, не зная о выборе игрока А. Третий ход делает игрок А, не зная выбора игрока В, но помня свой собственный ход. Функции выплат игроку А за счет игрока В задаются следующим образом:
Найдите оптимальные стратегии игроков и цену игры. 4. Два участника играют в некоторую игру. Первый ход делает игрок А, второй – игрок В, не зная о выборе игрока А. Третий ход делает игрок А, зная предыдущие ходы. Функции выплат игроку А за счет игрока В задаются следующим образом:
Найдите оптимальные стратегии игроков и цену игры. 5. Два участника играют в некоторую игру. Первый ход делает игрок А, второй – игрок В, не зная о выборе игрока А. Третий ход делает игрок А, не зная выбора игрока В, и забыв свой собственный ход. Функции выплат игроку А за счет игрока В задаются следующим образом:
Найдите оптимальные стратегии игроков и цену игры. 6. Два участника играют в некоторую игру. Первый ход производится случайным образом, второй ход делает игрок А, не зная результата за первый ход. Третий ход делает игрок В, зная какое число выпало на первом ходе и не зная какое на втором. Функции выплат игроку А за счет игрока В задаются следующим образом:
Найдите оптимальные стратегии игроков и цену игры. 7. Два участника играют в некоторую игру. Первый ход производится случайным образом, второй ход делает игрок А, не зная результата за первый ход. Третий ход делает игрок В, не зная какое число выпало на первом ходе, но зная какое на втором. Функции выплат игроку А за счет игрока В задаются следующим образом:
Найдите оптимальные стратегии игроков и цену игры. 8. Два участника играют в некоторую игру. Первый ход производится случайным образом. Если выпадает 1-ая альтернатива, то второй ход делает игрок А, зная результат первого хода, а третий ход делает игрок В, зная какое число выпало на первом ходе, но не зная какое на втором. Если выпадает 2-ая альтернатива, то второй ход делает игрок В, зная результат первого хода, а третий ход делает игрок А, зная какое число выпало на первом ходе, но не зная какое на втором. Функции выплат игроку А за счет игрока В задаются следующим образом:
Найдите оптимальные стратегии игроков и цену игры. 9. Первый игрок по своему выбору и незаметно от второго игрока прячет в кулаке одну из двух монет достоинством 1 или 5 рублей, а второй – пытается угадать, какая монета спрятана, и если угадывает, то получает эту монету, в противном случае платит первому игроку 3 рубля. Определите оптимальные стратегии игроков и цену игры. 10. Фирма А предлагает фирме В совместить два производства для получения большей прибыли. Фирма В, ознакомившись с предложением фирмы А, высказывает свои условия и встречные предложения, способные, по её мнению, заинтересовать фирму А. В свою очередь, фирма А, ознакомившись с реакцией фирмы В на сделанные предложения, высказывает ей новое предложение, внеся одну из нескольких возможных корректировок в свое первоначальное предложение с учетом мнения фирмы В. Найдите оптимальные стратегии фирм и цену игры, если функции выигрышей задаются следующим образом:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
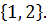
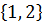 , зная число x, предложенное стороной А.
, зная число x, предложенное стороной А. :
:



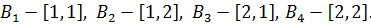
 где
где  – альтернатива, которую выбирает игрок А на первом ходе,
– альтернатива, которую выбирает игрок А на первом ходе, 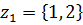 – альтернатива которую выбирает игрок А на третьем ходе, если на втором ходе игрок В выбрал первую альтернативу
– альтернатива которую выбирает игрок А на третьем ходе, если на втором ходе игрок В выбрал первую альтернативу  тогда
тогда  если В выбрал
если В выбрал 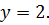
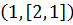 означает, что на 1-ом ходе игрок А выбирает
означает, что на 1-ом ходе игрок А выбирает 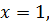 а на 3-ем –
а на 3-ем –  если игрок В выбрал
если игрок В выбрал  если игрок В выбрал
если игрок В выбрал 
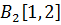









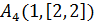




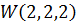
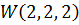

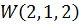
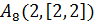
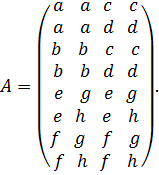
 соответственно – задаются следующим образом:
соответственно – задаются следующим образом:

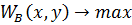

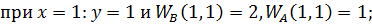

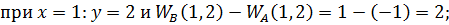

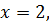 то игрок В получает право 2-го хода, где он и выбирает число y из множества двух чисел
то игрок В получает право 2-го хода, где он и выбирает число y из множества двух чисел  выигрыш игрока А равен 1, а игрока В – 4. При
выигрыш игрока А равен 1, а игрока В – 4. При  оба игрока получают поровну – по 3.
оба игрока получают поровну – по 3. и игра заканчивается. Но при
и игра заканчивается. Но при  каждый из игроков получает по 3 (такой исход предпочтительнее простейшего (2, 2)), и, если допустить соглашение между игроками, это обстоятельство вполне может изменить исход игры.
каждый из игроков получает по 3 (такой исход предпочтительнее простейшего (2, 2)), и, если допустить соглашение между игроками, это обстоятельство вполне может изменить исход игры.


 ,
, ,
,

 ,
, ,
,

 ,
,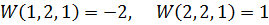 ,
,

 ,
, ,
,

 ,
, ,
,

 ,
, ,
,

 ,
, ,
,

 ,
, ,
,