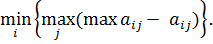|
|
Основные этапы поиска решения матричных игрМатричные игры моделируют конфликтные ситуации, в которых каждая из сторон-участниц делает свой ход одновременно со второй стороной. При этом наибольший интерес представляет случай, когда игра не заканчивается сразу же после совершения игроками одной такой пары одновременных ходов, а повторяется многократно. Причем считается, что перед каждым возобновлением игры игроки не получают никаких новых сведений ни о конфликте, ни о возможных действиях противной стороны. Иными словами, при многократном повторении матричной игры каждая из сторон всякий раз оказывается перед выбором некоторой стратегии из одного и того же множества стратегий, неизменного у каждого из игроков. Тем не менее, в таких многократно повторяющихся обстоятельствах большую роль играет анализ игры, как предварительный, так и промежуточный. В результате разумно проведенного предварительного анализа матричной игры, заинтересованная в нём сторона может определить свою линию поведения (правило выбора стратегий) на всю серию игр. Описанный выше максиминный подход является далеко не единственным средством нахождения оптимальных чистых стратегий. Однако не следует забывать, что принципиальной особенностью этого подхода является то обстоятельство, что игрок, придерживающийся выводимого на его основе правила выбора стратегий, заранее может довольно точно оценить нетривиальные размеры своего гарантированного выигрыша. Кроме того, максиминный подход позволяет сводить задачу поиска решения игры к рассмотрению сравнительно несложных задач линейного программирования и тем самым получать эффективные рекомендации, как лучше выбирать стратегии в конкретной игре при многократном её повторении. Если игра повторяется много раз, то некоторые дополнительные сведения – какие именно стратегии выбирает противная сторона и какими правилами выбора стратегий она руководствуется – игрок все же получает. На основании этих сведений и результатов предварительного анализа игры он может довольно точно оценить противника, и если тот не придерживается компромиссного минимаксного подхода, внести соответствующие изменения в собственную линию поведения и увеличить выигрыш. Сформулируем основные этапы поиска решения матричных игр: 1-й этап – проверка наличия или отсутствия равновесия в чистых стратегиях. При наличии равновесной ситуации указываются соответствующие оптимальные стратегии игроков и цена игры. 2-й этап – поиск доминирующих стратегий. В случае успеха этого поиска, отбрасываем доминируемые строки и столбцы в исходной матрице игры. 3-й этап – замена игры на её смешанное расширение и отыскание оптимальных смешанных стратегий и цены игры.
2.5. Примеры для самостоятельной работы 1. Найдите нижнюю цену игры, верхнюю цену игры, определите седловые точки, оптимальные чистые стратегии и цену игры:
2. В платежной матрице
указано, какую долю рынка выигрывает предприятие у своего единственного конкурента, если оно будет действовать согласно каждой из возможных трех стратегий, а конкурент – согласно каждой из своих возможных трех стратегий. Определите оптимальные стратегии предприятий и цену их игры. 3. В игре участвуют два игрока, каждый из которых может записать цифры 1, 2 и 3 независимо друг от друга. Если разность между цифрами, записанная игроками, положительна, то первый игрок выигрывает количество очков, равное разности между цифрами, и наоборот, если разность отрицательна, то выигрывает второй игрок. Если разность равна 0, то игра заканчивается вничью. Составьте платежную матрицу и определите оптимальные стратегии игроков и цену игры. 4. Найдите решения следующих матричных игр:
5. Обувная фабрика планирует выпуск двух моделей обуви А и В. Спрос на эти модели не определен, однако можно предположить, что он может принимать одно из двух состояний. В зависимости от этих состояний прибыль предприятия различна и определяется матрицей:
Найдите оптимальное соотношение между объемами выпуска каждой из моделей, при котором предприятию гарантируется средняя величина прибыли при любом состоянии спроса. 6. Два игрока А и В играют в игру, основанную на подбрасывании монеты. Игроки одновременно и независимо друг от друга выбирают: орёл либо решка. Если результаты двух подбрасываний монеты совпадают, то игрок А получает один доллар от игрока В. Иначе игрок А платит один доллар игроку В. Составьте матрицу выплат игрока В игроку А и найдите оптимальные стратегии игроков и цену игры. 7. Саша и Лиза договорились встретиться зимой возле кинотеатра. Если Саша придет раньше назначенного времени, то Лизы ещё не будет и ему придется мерзнуть. Потери свои в этом случае Саша оценивает -1. Если раньше придет Лиза, то ему будет ещё хуже, потери равны -4. В том случае, когда оба приходят одновременно, потерь нет ни у кого. Как быть Саше и Лизе? 8. Между двумя небольшими государствами А и В ведется война в течении 30 дней. Для бомбардировки небольшого моста – важного военного объекта страны В – страна А использует оба имеющихся у нее самолета. Разрушенный мост восстанавливается в течение суток, а каждый самолет совершает один полет в день по одному из двух воздушных маршрутов, соединяющих эти страны. У страны В есть два зенитных орудия, при помощи которых можно сбивать самолеты страны А. Если самолет собьют, то некая третья страна в течение суток поставит стране А новый самолет. Страна А может послать самолеты либо по одному маршруту, либо по разным. Страна В может поместить либо обе зенитки на одном маршруте, либо по одной зенитке на каждом маршруте. Если один самолет летит по маршруту, на котором расположена одна зенитка, то этот самолет будет сбит. Если два самолета летят по маршруту, на котором расположены две зенитки, то оба самолета будут сбиты. Если два самолета летят по маршруту, на котором расположена одна зенитка, то сбит будет только один самолет. Если самолет доберется до цели, то мост будет уничтожен. Определите оптимальные стратегии поведения стран А и В. 9. Используя графический метод, найдите решения игр, определяемых следующими матрицами:
10.Сельскохозяйственное предприятие имеет возможность выращивать две культуры. Необходимо определить, как сеять эти культуры, если при прочих равных условиях их урожаи зависят от погоды, а план посева должен обеспечить наибольший доход. В качестве выигрыша возьмем прибыль от реализации и будем считать, что расчеты прибыли сельскохозяйственного предприятия (в млн. руб.) в зависимости от трех состояний погоды: засушливое лето, нормальное лето и дождливое лето; сведены в следующую матрицу:
11. Используя правило доминирования, найдите решения следующих матричных игр:
12.Администрация некоторой фирмы ведет переговоры с профсоюзом рабочих и служащих о заключении контракта. Платежная матрица отражает интересы договаривающихся сторон:
Выплаты представляют собой среднюю зарплату служащего, т.е. данная матрица описывает прибыль профсоюза и затраты администрации. Определите наиболее оптимальное решение для обеих сторон. 13. Предприятие выпускает скоропортящуюся продукцию, которую может отправить потребителю, отправить на склад для хранения или подвергнуть дополнительной обработке. В свою очередь потребитель может немедленно приобрести эту продукцию, приобрести ее в течение небольшого отрезка времени или затребовать ее после длительного периода времени. Если предприятие выберет первую стратегию, то дополнительные затраты на хранение и обработку продукции не потребуются. Однако если при этом потребитель примет вторую стратегию или тем более третью, то предприятие потерпит убытки из-за порчи части продукции. Наоборот, если предприятие выберет вторую стратегию, а потребитель – первую, то возникнут неоправданные расходы на консервацию продукции. Определить оптимальное соотношение между продукцией, отправляемой потребителю, на склад и на дополнительную обработку для предприятия при соответствующей матрице затрат:
14. Используя метод линейного программирования, найдите решения следующих матричных игр:
15. Торговая фирма разработала несколько вариантов плана продажи товаров на предстоящей ярмарке с учетом меняющейся конъюнктуры рынка и спроса покупателей. Получающиеся от их возможных сочетаний показатели дохода представлены в следующей матрице:
Определите оптимальный план продажи товаров. 16. Швейное предприятие планирует к массовому выпуску новую модель одежды. Спрос на эту модель не может быть точно определен, однако можно предположить, что его величина характеризуется тремя возможными состояниями. С учетом этих состояний анализируется три возможных варианта выпуска данной модели (А, В, С). Каждый из этих вариантов требует своих затрат и обеспечивает в конечном счете различный эффект. Прибыль, которую получает предприятие при данном объеме выпуска модели и соответствующем состоянии спроса, определяется матрицей:
Требуется найти объем выпуска модели одежды, обеспечивающий среднюю величину прибыли при любом состоянии спроса. 17. Предприятие может выпускать три вида продукции А, Б, В, получая при этом прибыль зависящую от спроса. Спрос может принимать одно из трех состояний 1, 2, 3. В следующей матрице элементы 1 2 3
Найдите оптимальные пропорции в выпуске продукции, считая состояние спроса полностью неопределенным, гарантируя при этом среднюю величину прибыли при любом состоянии прибыли. 18. Используя матричный способ, найти решение следующих игр:
19. Найдите приближенные решения следующих матричных игр:
ГЛАВА 3. ИГРЫ С “ПРИРОДОЙ”
Основные понятия и критерии В рассмотренных выше матричных играх предполагалось, что в них принимают участие два игрока, интересы которых противоположны. Поэтому действия каждого игрока направлены на увеличение выигрыша (уменьшение проигрыша). Однако в некоторых задачах, приводящихся к игровым, имеется неопределенность, вызванная отсутствием информации об условиях, в которых осуществляется действие (погода, покупательский спрос и т. д.). Эти условия зависят не от сознательных действий другого игрока, а от объективной действительности. Такие игры называются играми с “природой”. Человек в играх с “природой” старается действовать осмотрительно, второй игрок (природа, покупательский спрос) действует случайно. Условия игры задаются матрицей
. Пусть игрок А имеет стратегии А1, А2, … , Аm, а природа – состояния B1, B2,…, Bn. Наиболее простым является ситуация, когда известна вероятность pj каждого состояния природы Bj. При этом если учтены все возможные состояния, то
Если игрок А выбирает чистую стратегию А1, то математическое ожидание выигрыша составит
Наиболее выгодной будет та стратегия, при которой достигается
Если информация о состояниях природы мала, то можно применить принцип недостаточного основания Лапласа, согласно которому можно считать, что все состояния природы равновероятны
т. е. стратегию, для которой среднее арифметическое элементов соответствующей строки максимальное. 1. Критерий Вальде. Рекомендуется применять максиминную стратегию. Она достигается из условия
и совпадает с нижней ценой игры. Критерий является пессимистическим, считается, что природа будет действовать наихудшим для человека способом. 2. Критерий максимума. Критерий является оптимистическим, считается, что природа будет благоприятна для человека и выбирается из условия
3. Критерий Гурвица. Критерий рекомендует стратегию, определяемую по формуле
где a - степень оптимизма и изменяется в диапазоне [0, 1]. Критерий придерживается некоторой промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего поведения природы. При a = 1 критерий превращается в критерий Вальде, при a = 0 – в критерий максимума. На a оказывает влияние степень ответственности лица, принимающего решение по выбору стратегии. Чем больше последствия ошибочных решений, больше желания застраховаться, тем a ближе к единице. 4. Критерий Сэвиджа. Суть критерия состоит в выборе такой стратегии, чтобы не допустить чрезмерно высоких потерь, к которым она может привести. Находится матрица рисков, элементы которой показывают, какой убыток понесет человек (фирма), если для каждого состояния природы он не выберет наилучшей стратегии. Элемент матрицы рисков находится по формуле
где Оптимальная стратегия находится из выражения:
При принятии решений в условиях неопределенности следует оценивать различные варианты с точки зрения нескольких критериев. Если рекомендации совпадают, можно с большей уверенностью выбрать наилучшее решение, если рекомендации противоречат друг другу, окончательное решение надо принимать с учетом его сильных и слабых сторон.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
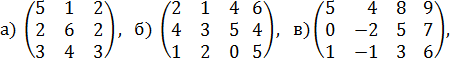
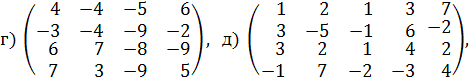


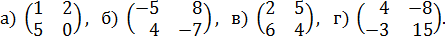
 .
.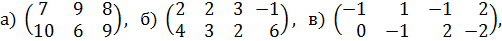
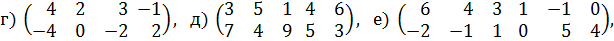
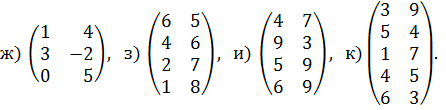
 .
.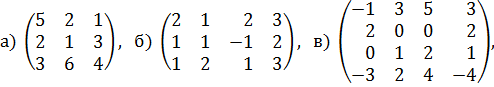
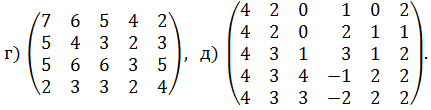
 .
. .
.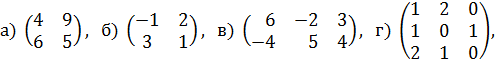
 .
.
 .
.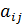 характеризуют прибыль, полученную предприятием при выпуске i-ой продукции и j-ым состоянием спроса:
характеризуют прибыль, полученную предприятием при выпуске i-ой продукции и j-ым состоянием спроса: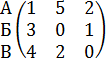 .
.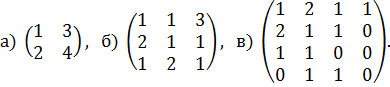

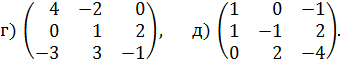
 .
.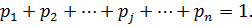
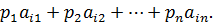
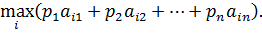
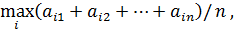

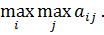
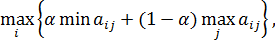
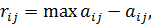
 - максимальный элемент в столбце исходной матрицы.
- максимальный элемент в столбце исходной матрицы.