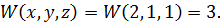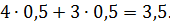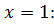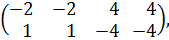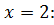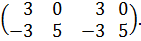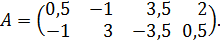|
|
Нормализация позиционной игрыЗаранее определенную последовательность хода игрока, выбранную им в зависимости от информации о ходах другого игрока и ходах игрока О, будем называть чистой стратегией этого игрока. В этом случае, если в игре нет случайных ходов, выбор игроками А и В чистых стратегий однозначно определяет исход игры. Это обстоятельство позволяет сводить позиционную игру к матричной игре. Процесс сведения позиционной игры к матричной называется нормализацией позиционной игры. Пример 1. Рассмотрим позиционную игру, состоящую из двух ходов, которые последовательно делают участвующие в ней игроки А и В. Первый ход делает игрок А, второй – игрок В, зная о выборе игрока А. Функции выплат игроку А за счет игрока В задаются следующим образом:
Найдите оптимальные стратегии игроков и цену игры. Решение. Определим ходы игроков и построим дерево рассматриваемой игры. 1-ый ход делает игрок А: выбирает один из двух возможных вариантов – число x из множества чисел 2-ой ход делает игрок В: выбирает число y из множества Изобразим графически данную игру:
У игрока А существует две стратегии Игрок В знает выбор игрока А на первом ходе, значит существует четыре стратегии Например, выбор игроком В стратегии Покажем теперь, как рассчитываются выигрыши игрока А в зависимости от примененных стратегий. Пусть, например, игрок А выбрал стратегию А1 – (1), а игрок В – стратегию В2 –
Остальные выигрыши рассчитываются аналогично. Результаты расчетов записываются в виде таблицы выигрышей игрока А: Таблица № 1.
Перейдем от таблицы №1 к матрице
Строки полученной матрицы соответствуют стратегиям игрока А, а столбцы – стратегиям игрока В. Данная игра имеет седловую точку, так как Пример 2. Рассмотрим случай, если выполнены все условия предыдущего примера, кроме одного – хода игрока В. Второй ход делает игрок В, не зная о выборе игрока А. Функции выигрышей игрока А возьмем аналогично примеру 1. Необходимонайти оптимальные стратегии игроков и цену игры. Решение. Определим ходы игроков и построим дерево рассматриваемой игры. 1-ый ход делает игрок А: выбирает один из двух возможных вариантов – число x из множества чисел 2-ой ход делает игрок В: выбирает число y из множества Изобразим графически данную игру:
У игрока А существует две стратегии Игрок В не знает выбор игрока А на первом ходе, значит существует две стратегии Составим таблицу выигрышей для игрока А: Таблица № 2.
Перейдем от таблицы № 2 к матрице
Полученная матрица не имеет седловой точки. Оптимальные смешанные стратегии игроков и цену игры можно найти, используя аналитический метод решения матричных игр, рассмотренный в предыдущей главе:
Пример 3. Усложним пример 1, добавив ещё один ход игроку А. Первый ход делает игрок А, второй – игрок В, зная о выборе игрока А. Третий ход делает игрок А, не зная выбора игрока В и забыв свой собственный ход. Функции выплат игроку А за счет игрока В задаются следующим образом:
Найдите оптимальные стратегии игроков и цену игры. Решение. Определим ходы игроков и построим дерево рассматриваемой игры. 1-ый ход делает игрок А: выбирает один из двух возможных вариантов – число x из множества чисел 2-ой ход делает игрок В: выбирает число y из множества 3-ий ход делает игрок А: выбирает число z из множества Тогда дерево игры имеет вид:
Нормализуем данную игру. Поскольку игроку В выбор игрока А на первом ходе известен, значит существует четыре стратегии: Игрок А на третьем ходе не знает предыдущих выборов – ни значения x, ни значения y. Поэтому каждая его стратегия состоит просто из пары чисел Например, выбор игроком А стратегии (2,1) означает, что на первом ходе он выбирает Покажем теперь, как рассчитываются выигрыши игрока А в зависимости от стратегий, применяемых игроками в данной игре. Пусть, например, игрок А выбрал стратегию
В результате подобных рассуждений получаются и остальные пятнадцать выигрышей. Составим таблицу выигрышей для игрока А: Таблица № 3.
Перейдем от таблицы № 3 к матрице
Полученная матрица имеет решение в смешанных стратегиях, так как Пример 4. Рассмотрим позиционную игру, состоящую из трёх ходов, первый из которых производится случайным образом. Второй ход делает игрок А, не зная результатов случайного выбора. Третий ход делает игрок В, зная результат случайного выбора на первом ходе и не зная выбора игрока А на втором ходе. Функцию Найдите оптимальные стратегии игроков и цену игры. Решение. Определим ходы игроков и построим дерево рассматриваемой игры. 1-ый ход производится случайно: игрок О выбирает число x, равное 1 с вероятностью 0,5 и равное 2 с такой же вероятностью. 2-ой ход делает игрок А: выбирает число y из множества 3-ий ход делает игрок В: выбирает число z из множества Графическое представление этой игры имеет вид: g rvi7sHjlZvWTYhGs44RtLrYnQo42sJYq4EFtQOdijfL5XqTFZrlZziazfLGZzNKmmdxt69lksc3e zZubpq6b7Eegls3KTjDGVWD3IuVs9ndSuTyqUYRXMV/bkLxGj40Gsi//kXQceJjxqJa9ZuedDa0N swf1RufLSwvP49d99Pr5PVg/AwAA//8DAFBLAwQUAAYACAAAACEAQW2P2OAAAAAJAQAADwAAAGRy cy9kb3ducmV2LnhtbEyPQU/CQBCF7yb+h82YeDGwBaFI7ZYYE4mEgxGI5213bBu6s013odVfz3DS 25u8L2/eS1eDbcQZO187UjAZRyCQCmdqKhUc9m+jJxA+aDK6cYQKftDDKru9SXViXE+feN6FUnAI +UQrqEJoEyl9UaHVfuxaJPa+XWd14LMrpel0z+G2kdMoiqXVNfGHSrf4WmFx3J2sglm8z9d9gZuF /Pjtzfb9a715sErd3w0vzyACDuEPhmt9rg4Zd8rdiYwXjYL5cjZllI3FEgQDcXQVOYvHGGSWyv8L sgsAAAD//wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAAAAAAAAAAAAAAAAAAAFtD b250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAACwAAAAAAAAAAAAAA AAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEA/55BiTMCAABXBAAADgAAAAAAAAAAAAAA AAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAQW2P2OAAAAAJAQAADwAAAAAAAAAA AAAAAACNBAAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAAJoFAAAAAA== "/>i E0t/c8zqvWIRrOWErS62J0KebUguVcCD2oDOxTrL58c8na9mq9loMMonq8EorevBw7oaDSbrbDqu 7+qqqrOfgVo2KlrBGFeB3VXK2ejvpHK5VGcR3sR8a0PyGj32C8he35F0HHiY8VktW81OG3sVAqg3 Hr7ctHA9Xu7Bfvk/WP4CAAD//wMAUEsDBBQABgAIAAAAIQB7l3ec3wAAAAkBAAAPAAAAZHJzL2Rv d25yZXYueG1sTI/BSsNAEIbvgu+wjOBF7CZG0jbNpohgsXgobaXnTXZMgtnZkN020ad3POlthu/n n2/y9WQ7ccHBt44UxLMIBFLlTEu1gvfjy/0ChA+ajO4coYIv9LAurq9ynRk30h4vh1ALLiGfaQVN CH0mpa8atNrPXI/E7MMNVgdeh1qaQY9cbjv5EEWptLolvtDoHp8brD4PZ6vgMT2Wm7HC7Vzuvkfz 9nrabO+sUrc309MKRMAp/IXhV5/VoWCn0p3JeNEpSKIk5SiD+RIEB5I45qFUkDKQRS7/f1D8AAAA //8DAFBLAQItABQABgAIAAAAIQC2gziS/gAAAOEBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVu dF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAALwEA AF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAMRp5jcvAgAAVwQAAA4AAAAAAAAAAAAAAAAALgIA AGRycy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhAHuXd5zfAAAACQEAAA8AAAAAAAAAAAAAAAAA iQQAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPMAAACVBQAAAAA= "/>
Опишем стратегии игроков. Поскольку игроку А исход случайного испытания неизвестен, то он имеет всего две стратегии: При построении своих стратегий игроку В естественно воспользоваться имеющейся у него информацией о результатах 1-го хода. Это позволит ему описать свою стратегию упорядоченной парой Покажем теперь, как определяются элементы таблицы выигрышей игрока А. Пусть, например, игрок А выбрал стратегию Различают два случая: 1) 2) Если
Если
Поскольку первая и вторая альтернативы на первом ходе выбираются с вероятностями 0,5 и 0,5, то и вышеуказанные выигрыши появляются с теми же вероятностями и, следовательно, средний выигрыш игрока А при этих стратегиях определяется так:
Аналогичным образом, рассчитывая остальные средние выигрыши, получим при Таблица № 4.
или
при Таблица № 5.
или
Отсюда получаем искомую матрицу игры:
Полученная матричная игра не имеет седловой точки, значит, решение необходимо искать в смешанных стратегиях. Проделать самостоятельно.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


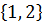 .
. : при выборе первой альтернативы
: при выборе первой альтернативы  , при выборе второй альтернативы
, при выборе второй альтернативы  .
. , где
, где  – альтернатива, выбираемая игроком В при условии, что игрок А выбрал первую альтернативу
– альтернатива, выбираемая игроком В при условии, что игрок А выбрал первую альтернативу  – альтернатива игрока В, при условии выбора игроком А второй альтернативы
– альтернатива игрока В, при условии выбора игроком А второй альтернативы 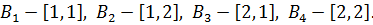
 означает, что если на первом ходе игрок А выбрал стратегию
означает, что если на первом ходе игрок А выбрал стратегию  , если же игрок А выбирает
, если же игрок А выбирает 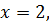 то игрок В
то игрок В 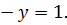
 Тогда
Тогда  вытекает, что
вытекает, что  Отсюда
Отсюда

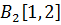








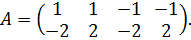
 Оптимальные стратегии игроков: А1 – (1) и В3 –
Оптимальные стратегии игроков: А1 – (1) и В3 – 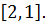 Тем самым игрок А на 1-ом ходе выбирает
Тем самым игрок А на 1-ом ходе выбирает 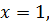 а игрок В на 2-ом ходе выбирает
а игрок В на 2-ом ходе выбирает 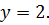 Цена игры
Цена игры 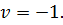
 ,
, 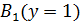


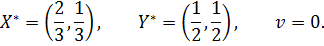




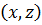 , где
, где  – альтернатива, выбираемая игроком А на 1-ом ходе, а
– альтернатива, выбираемая игроком А на 1-ом ходе, а 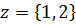 – альтернатива, выбираемая игроком А на 3-ем ходе.
– альтернатива, выбираемая игроком А на 3-ем ходе. . Таким образом, у игрока А четыре стратегии:
. Таким образом, у игрока А четыре стратегии: 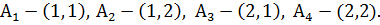
 , а игрок В – стратегию
, а игрок В – стратегию  . Тогда
. Тогда  . Значение
. Значение  выбрано игроком А независимо от выбора игрока В. Вычисляя значение функции выигрышей для этого набора, получаем
выбрано игроком А независимо от выбора игрока В. Вычисляя значение функции выигрышей для этого набора, получаем
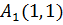








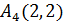
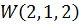
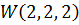
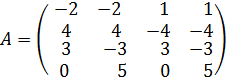 .
. . Найти самостоятельно.
. Найти самостоятельно. выплат игроку А используем ту же, что и в предыдущем примере.
выплат игроку А используем ту же, что и в предыдущем примере.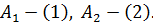
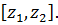 Здесь
Здесь 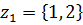 – альтернатива, выбираемая игроком В при условии, что
– альтернатива, выбираемая игроком В при условии, что  – альтернатива, выбираемая игроком В при условии, что
– альтернатива, выбираемая игроком В при условии, что  а игрок В – стратегию
а игрок В – стратегию 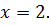
 указывает игроку В его выбор
указывает игроку В его выбор  А так как
А так как  то в результате имеем
то в результате имеем
 А так как
А так как