
|
|
Общие понятия алгоритма и вычислимой функции.Для каждого алгоритма A имеется множество DA возможных исходных данных этого алгоритма. В результате применения A к любому xÎDA возможны три исхода: 1) применение A к x закончится за конечное число шагов и алгоритм выдаст результат A(x), 2) применение алгоритма A к значению x закончится без какого-либо результата, 3) применение алгоритма A к значению x ничем не закончится. В первом случае говорят, что алгоритм A применим к значению x, и в остальных двух случаях - что алгоритм A не применим к значению x. Множество всех xÎDA , к которым применим алгоритм A, называется областью применения алгоритма A . Для алгоритма A на множестве DA определяется частичная функция f со значениями f(x)=A(x) для всех значений xÎDA , принадлежащих области применения алгоритма A. В этом случае принято говорить, что алгоритм A вычисляет частичную функцию f. Функция называется вычислимой, если существует вычисляющий ее алгоритм. Понятие алгоритма имеет смысл лишь в том случае, если множество его возможных исходных данных является потенциально обозримым множеством, которое состоит из последовательно конструируемых объектов. Примеры: N и А* . Далее при изучении алгоритмов A и вычислимых функций Аксиома: для любых двух таких множеств X,Y существует вычислимая биекция X на Y. Пример. Сопоставление последовательно конструируемых элементов множеств N0и А* определяет вычислимую биекцию f : N ® А* по правилу:
Подмножество A множества X называется разрешимым (или рекурсивным), если имеется алгоритм, который для любого элемента xÎX позволяет определить, является x элементом множества A или нет. Другими словами, A разрешимо, есливычислима характеристическая функция Свойства: дополнения, конечные пересечения и конечные объединения разрешимых множеств являются разрешимыми множествами. Подмножество A множества X называется перечислимым, если оно пусто или является областью применения некоторого алгоритма. Другими словами, непустое множество A перечислимо, еслиимеется алгоритм, который применим к элементам множества A и не применим к элементам множества X\A. Теорема. Непустое подмножество A множества X в том и только том случае перечислимо, если оно является множеством значений всюду определенной вычислимой функции f:N ® X. Свойства: конечные пересечения и конечные объединения перечислимых множеств являются перечислимыми множествами. Теорема Поста. Подмножество A множества X в том и только том случае разрешимо, если A и X\A перечислимы. Теорема. Функция f из X в Y вычислима в том и только том случае, если ее график Теорема об универсальной функции. Пусть F называется универсальной функцией для множества функций Для множества По определению Значит, номер m не может принадлежать области определения функции f. Таким образом, f не является всюду определенной функцией на множестве N. Пусть g:N®N – всюду определенная функция, которая является продолжением частичной функции f, т.е. для любых n из области определения функции f выполняется равенство Тогда Теорема. Существует вычислимая частичная функция f из N в N, которая не имеет всюду определенного вычислимого продолжения на все множество N. Следствие. Существует перечислимое неразрешимое множество. Другими словами, существует алгоритм A с множеством возможных исходных данных N, для которого алгоритмически неразрешима следующая задача: «определить по данному xÎN, применим ли алгоритм A к значению x»? Формальные грамматики Определение. Грамматикой называется алгебраическая система Правила грамматики позволяют преобразовать слова ее полного словаря. Для любого g0ÎG образуется некоторое множество слов Определение. Пусть у,z ÎV* – слова над полным словарем V грамматики - слово z непосредственно выводится из слова у и писать - слово z выводится из слова у и писать Определение. Для произвольно фиксированного грамматического символа g0ÎG множество всех слов над алфавитом А, которые выводятся из g0, обозначается Таким образом, по определению
Примеры. 1. Пусть грамматика Схематически процесс построения языка
2. Пусть грамматика
В качестве еще одного применения грамматик рассмотрим общепринятый подход к языкам программирования на примере построения известного языка ALGOL 60. Алфавит А такого языка состоит из букв, цифр, алгебраических символов и специальных зарезервированных слов, его грамматическими символами являются некоторые подмножества множества А* и, наконец, имеются определенные грамматические правила, по которым строятся программы этого языка. Грамматика А={А,В,...,Z,а,b,...,z,0,1,…,9,+,-,*,/,¸,,=,¹,<,£,>,³,Ù,Ú,º,;,×,:,(,),[,], BEGIN, TRUE, FALSE, GOTO, FOR, STEP, UNTIL, END} и множеством грамматических символов G, состоящим из множеств I,U,R,В,D,L,… подмножеств множества A*, которые обозначаются символами <идентификатор>, <целое без знака>, <вещественное>, <булево>, <цифра>, <буква>,… и неявно определяются последовательностью уравнений вида: I = L È IL È ID, U = D È UD и т.д., где IL,ID,UD – произведения подмножеств в полугруппе слов А*. Эти уравнения определяются соответствующими правилами языка ALGOL: <идентификатор> ::= <буква> | <идентификатор><буква> | <идентификатор><цифра>, <число без знака> ::= <цифра>|<число без знака><цифра>, … Пусть g0 – произвольный начальный символ, удовлетворяющий условию g0ÏA и p – множество правил грамматики вида: g0®I, g0®g0D, g0®g07и т. п. Языки, порождаемые такими грамматиками с произвольным конечным алфавитом А и определяемым уравнениями множеством грамматических символов GÌА*, называются языками типа ALGOL. Определение. Язык LÌA+называется языком, порожденным грамматикой (или языком типа 0), если Теорема 1. Язык LÌA+в том и только том случае порождается некоторой грамматикой, если он последовательно порождается некоторой эффективной процедурой (алгоритмом) P, т.е. Такие языки называются рекурсивно перечислимыми. Определение. Грамматика - контекстно-зависимой (или типа 1), если любое ее правило имеет вид - контекстно-свободной (или типа 2), если любое ее правило имеет вид - праволинейной (или рациональной, или типа 3), если любое ее правило имеет вид Для каждого типа Теорема 2. Язык LÌA+в том и только том случае порождается некоторой контекстно-зависимойграмматикой, если найдется такая эффективная процедура (алгоритм), которая для любого слова wÎA+ позволяет определить, принадлежит ли это слово языку L или нет. Такие языки называются рекурсивными. Теорема 3. Язык LÌA+в том и только том случае порождается некоторой контекстно-свободнойграмматикой, если он является языком типа языка программирования ALGOL. Теорема 4. Язык LÌA+в том и только том случае порождается некоторой праволинейнойграмматикой, если он получается из однобуквенных языков Такие языки называются рациональными, поскольку они определяются формулами с постоянными символами Так как конструктивные объекты можно кодировать словами конечного множества A (например, состоящего из двоичных символов 0 и 1), то алгоритм моделируется устройством, перерабатывающим слова алфавита A. Пусть А – произвольное конечное множество, называемое алфавитом. Элементы aÎА называются буквами. Словом над алфавитом А называется конечная последовательность букв Слово без букв называется пустым словом и обозначается символом Обозначим символом На этих множествах определена операция умножения слов по следующему правилу: любым двум словам
полученное в результате приписывания к первому слову Подмножества множества 1) сложение K+L = { u : u Î K или u Î L }; 2) умножение итерация 1. Для однобуквенного алфавита A={a} словами являются последовательности: a, aa, aaa, … В этом случае множества слов Языками над алфавитом A={a} являются всевозможные множества слов, образованных из одной буквы a. 2. Для двухэлементного алфавита A={a,b} словами являются последовательности: a, b, aa, ab, ba, bb,… В этом случае множество слов Языками над алфавитом A={a,b} являются всевозможные множества слов, образованных из двух букв a,b. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
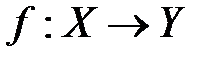 будем предполагать, что соответствующие множества DA,X,Y являются потенциально обозримым бесконечными множествами последовательно конструируемых объектов.
будем предполагать, что соответствующие множества DA,X,Y являются потенциально обозримым бесконечными множествами последовательно конструируемых объектов. и
и  , если
, если  и
и  – представление натурального числа x в p–ичной системе со значениями
– представление натурального числа x в p–ичной системе со значениями 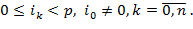
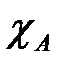 этого множества.
этого множества.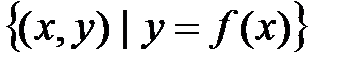 является перечислимым подмножеством множества X´Y.
является перечислимым подмножеством множества X´Y. - множество всех вычислимых функций из X в Y . Тогда найдется такая вычислимая функция F изN´X в Y, что для любой функции
- множество всех вычислимых функций из X в Y . Тогда найдется такая вычислимая функция F изN´X в Y, что для любой функции 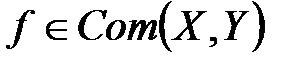 найдется такое nÎN, что f совпадает с частичной функцией
найдется такое nÎN, что f совпадает с частичной функцией  из X в Y.
из X в Y.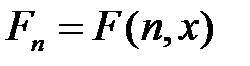 , называется номером f относительно универсальной функции F и соответствие
, называется номером f относительно универсальной функции F и соответствие  называется нумерацией вычислительных функций, соответствующей универсальной функции F.
называется нумерацией вычислительных функций, соответствующей универсальной функции F. всех вычислимых функций из N в Nнайдется универсальная вычислимая функция G изN´Nв N. Тогда уравнение
всех вычислимых функций из N в Nнайдется универсальная вычислимая функция G изN´Nв N. Тогда уравнение 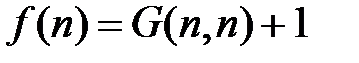 определяет вычислимую функцию из N в N,которая имеет некоторый номер m относительно универсальной функции G, т.е.
определяет вычислимую функцию из N в N,которая имеет некоторый номер m относительно универсальной функции G, т.е.  .
. 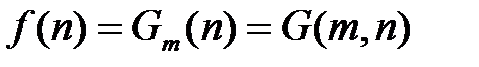 для всех n из области определения функции f.
для всех n из области определения функции f. .
. .
. , состоящая из непустых конечных множеств А,G иконечного бинарного отношения p между словами из множества G+ и словами из множества (AÈG)* . Множество А называется алфавитом грамматики имножество V=AÈG – полным словарем грамматики. Элементы множества G не принадлежаталфавиту А и называются грамматическими (или металингвистическими) символами грамматики. Элементы (u,v)Îp отношения p называются правилами грамматики и символически обозначаются u®v . В этом случае говорят, что слово v получается из слова u по правилу p.
, состоящая из непустых конечных множеств А,G иконечного бинарного отношения p между словами из множества G+ и словами из множества (AÈG)* . Множество А называется алфавитом грамматики имножество V=AÈG – полным словарем грамматики. Элементы множества G не принадлежаталфавиту А и называются грамматическими (или металингвистическими) символами грамматики. Элементы (u,v)Îp отношения p называются правилами грамматики и символически обозначаются u®v . В этом случае говорят, что слово v получается из слова u по правилу p. .
. . Будем говорить, что:
. Будем говорить, что: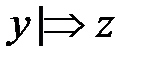 ,если z можно получить из у заменой некоторого его подслова u на слово w по некоторому правилу грамматики u®w,;
,если z можно получить из у заменой некоторого его подслова u на слово w по некоторому правилу грамматики u®w,; ,если z можно получить из слова у конечным числом замен некоторых подсловпо некоторым правилам грамматики.
,если z можно получить из слова у конечным числом замен некоторых подсловпо некоторым правилам грамматики.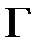 и начальным символом g0ÎG.
и начальным символом g0ÎG.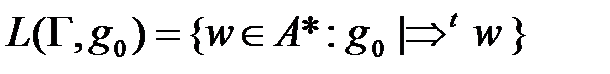 .
. ,a5,
,a5,  ,…}.
,…}.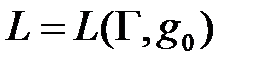 для некоторой грамматики
для некоторой грамматики  , где каждый элемент
, где каждый элемент  является результатом применения процедуры P к последовательным значениям
является результатом применения процедуры P к последовательным значениям 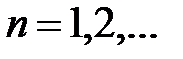 .
.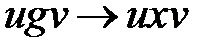 для некоторых
для некоторых 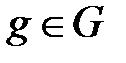 ,
,  ,
, 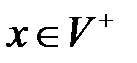 ;
;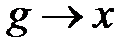 для некоторых
для некоторых 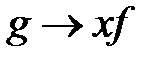 или
или  для некоторых
для некоторых 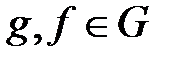 и
и  .
.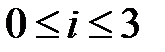 обозначим Ki класс всех языков, порожденных грамматиками типа i. Известно, что
обозначим Ki класс всех языков, порожденных грамматиками типа i. Известно, что  , причем все эти включения строгие.
, причем все эти включения строгие.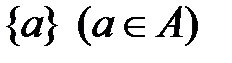 с помощью алгебраических операций сложение +, умножение × и итерация +.
с помощью алгебраических операций сложение +, умножение × и итерация +. и символами трех алгебраических операций +, × и +. Например, рациональный язык в примере 2 определяется формулой
и символами трех алгебраических операций +, × и +. Например, рациональный язык в примере 2 определяется формулой  .
. алфавита А.
алфавита А.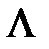 .
. множество всех непустых слов над алфавитом и символом
множество всех непустых слов над алфавитом и символом 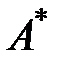 – множество слов
– множество слов  .
.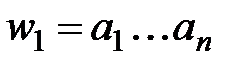 ,
, 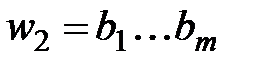 ставится в соответствие слово
ставится в соответствие слово ,
, второго слова
второго слова 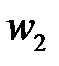 .
. и
и  ;
;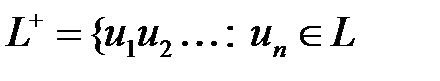 для всех nÎN}. Примеры.
для всех nÎN}. Примеры.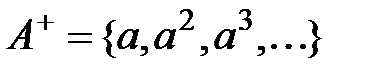 и
и  являются бесконечными множествами, которые позволяют кодировать сколь угодно большие конечные множества B с помощью отображений
являются бесконечными множествами, которые позволяют кодировать сколь угодно большие конечные множества B с помощью отображений  .
. и
и  также бесконечны.
также бесконечны.