
|
|
Логическая равносильность формул алгебры предикатовОпределение. Формулы алгебры предикатов В этом случае записывают Таким образом, Лемма 3. Пусть формула Тогда формулы
Теорема 4 (Законы де Моргана для кванторов). Для любой формулы
Теорема 5 (Взаимосвязь кванторов с конъюнкцией и дизъюнкцией). Для любых формул
Если в
Теорема 6 (Взаимосвязь кванторов с импликацией). Если в формулу
Если же предметная переменная x не входит свободно в формулу
Следствие 7. Любая формула
где Таким образом, каждая формула Теорема (Взаимосвязь между кванторами). Для любой формулы
С другой стороны, если в формулу
не выполняется, так как в этом случае формула не является тавтологией. Логическое следование формул алгебры предикатов С помощью логического следования формул определяются общие способы доказательства взаимосвязи между истинностными значениями утверждений посредством исследования формальной структуры этих утверждений. Определение. Формула Определение. Формула Такое логическое следствие обозначается В случае, когда
Определение. Множество формул Лемма 1 (Критерии логического следования). Условие d) e) f) В частности, Основные правила логического следования: 1) правило отделения (или правило модус поненс – от латинского modus ponens)
2) правило модус толленс (от латинского modus tollens)
3) правило контрапозиции
4) правило цепного заключения
Формальные исчисления Альтернативой семантического подхода является синтаксический подход, при котором логические формулы выводятся из первоначально выделенного множества формул – аксиом по определенным правилам преобразования формул логического языка без привлечения вспомогательных теоретико-множественных понятий. В этом случае полностью отвлекаются от содержания логических формул, и построение математической логики осуществляется в виде некоторого формального исчисления I, которое в общем случае определяется следующим образом: 1) задается алфавит исчисления A(I), который состоит изосновных символов исчисления I, и рассматривается множество W(I) всех слов над этим алфавитом; 2) выделяется подмножество E(I) Ì W(I) правильно построенных формул исчисления I; 3) задается подмножество Ax(I) Ì E(I) аксиом исчисления I;
4) рассматривается конечное множество R(I) частичных операторов R1, ,…, Rn на множестве формул E(I), которые называются правилами вывода исчисления I; 5) описывается алгоритм вывода из аксиом теорем исчисления I; 6) множество всех таких теорем образует теорию Th(I) формального исчисления I, которая называется также аксиоматической теорией с множеством аксиом Ax(I). Аксиоматическая теория Th(I) называется: - полной, если Th(I) совпадает с множеством тождественно истинных формул формального исчисления I, - непротиворечивой, если она не содержит никакой формулы F формального исчисления I вместе с ее отрицанием ØF, - разрешимой, если существует такая универсальная эффективная процедура (алгоритм), которая позволяет для любой формулы F формального исчисления I определить, будет или нет эта формула теоремой исчисления I.
Построение математических теорий в виде аксиоматических теорий соответствующих формальных исчислений составляет суть аксиоматического метода в математике. Простейшей аксиоматической теорией является аксиоматическая логика высказываний, которая строится на основе соответствующего формального исчисления, называемого исчислением высказываний (сокращенно, ИВ). Исчисление высказываний Множество аксиом Ax(ИВ)исчисления высказываний описывается следующими тремя схемами аксиом:
где Исчисление высказываний имеет единственное правило вывода, которое называется правилом заключения или правилом modus ponens (сокращенно MP) и которое для произвольных формул исчисления высказываний Символически это правило вывода записывается следующей схемой:
В основе алгоритма вывода теорем исчисления высказываний лежит следующее понятие. Определение. Формула F называется теоремой исчисления высказываний, если найдется такая конечная последовательность формул 1) 2) каждая формула Последовательность формул Вывод формулы F сокращенно обозначают символом |-F и говорят, что «F есть теорема». Множество всех таких теорем обозначается символом Th(ИВ) и называется теорией исчисления высказываний. Главной целью построения исчисления высказываний является определение такой теории Th(ИВ), которая совпадает с множеством тавтологий TАВ. Понятие вывода формул из аксиом обобщается на вывод из произвольного множества формул Γ. Определение. Формула F называется следствием множества формул Γ, если найдется конечная последовательность формул
Вывод обозначают символом Γ|-F и говорят, что «F есть следствие Γ». Элементы Γ называются гипотезами или посылками вывода, и формула Φ называется следствием вывода. Основные свойства понятия выводимости: 1) Γ|-F равносильно тому, что 2) если Γ является подмножеством множества формул Δ и Γ|-F, то Δ|-F; 3) если Γ|-F и Δ|-Ψ для любой формулы ΨÎΓ, то Δ|-Φ; 4) если Γ|-F и все формулы из Γ являются теоремами, то Φ – теорема. Теорема дедукции. Пусть Φ,Ψ – формулы исчисления высказываний и Γ – такое множество формул исчисления высказываний, что Γ,Φ|-Ψ. Тогда Γ |- Доказательство. Пусть При Так как по В третьем случае по теореме |- Предположим, что Γ |- В первых трех случаях по аналогии с предыдущим легко показать, что Γ |- В последнем случае по определению правила вывода MP формула Таким образом, Γ |- Лемма 1. Справедливы следующие утверждения: (i) |- (ii) |- (iii) |- (iv) |- (v) |- (vi) |- (vii) |- Лемма 2. Пусть формула Φ зависит от пропозициональных переменных
Доказательство. По определению Докажем (1) индукцией по числу n вхождения в формулу Φ пропозициональных связок Если n=0, то формула Φ не имеет пропозициональных связок, т.е. просто является пропозициональной переменной Предположим, что для всех формул с числом вхождения пропозициональных связок Если
Если Если же
т.е. для Φ верно (1). Если
Аналогично с помощью свойств из леммы 1 получаем, что для формулы Φ верно (1). Лемма 3. Справедливы следующие утверждения: 1)всякая аксиома ИВ является тавтологией; 2)результат применения правила вывода MP к любым тавтологиям 3)всякая теорема ИВ является тавтологией, т.е. выполняется Th(ИВ)ÌTАВ. Теорема полноты ИВ. Всякая тавтология является теоремой ИВ, т.е. выполняется TАВÌTh(ИВ) и, следовательно, TАВ=Th(ИВ). Доказательство. Пусть Φ - тавтология, зависящая от пропозициональных переменных
При По теореме дедукции
При
По свойству (vii) леммы 1 |- Дважды применяя правило вывода MP, получаем
Следствия теоремы полноты ИВ. Теорема о непротиворечивости ИВ. В исчислении высказываний невозможно доказать никакую формулу F вместе с ее отрицанием ØF. Теорема о разрешимости ИВ. Существует универсальная эффективная процедура (алгоритм), которая для любой формулы определяет, является ли эта формула теоремой ИВ. Исчисление предикатов Множество аксиом Ax(ИП)исчисления предикатов описывается пятью схемами аксиом – тремя определенными в предыдущем разделе схемами
для произвольной формулы
для таких формул Исчисление предикатов имеет два правила вывода – правило modus ponens (сокращенно, MP) и правило обобщения (сокращенно, Gen), которые для произвольных формул исчисления предикатов
Определение. Формула F называется теоремой исчисления предикатов, если найдется такая последовательность Вывод формулы F обозначают |-F и говорят, что «F есть теорема». Множество всех таких теорем обозначается символом Th(ИП) и называется теорией исчисления предикатов. Цель построения исчисления предикатов - определение такой теории Th(ИП), которая совпадает с множеством тавтологий TАП. Лемма 1. Справедливы следующие утверждения: 1)всякая аксиома ИП является тавтологией; 2)результат применения правил вывода MP и Gen к тавтологиям является тавтологией; 3)любая теорема ИП является тавтологией АП, т.е. имеет место включение Th(ИП)ÌTАП. Доказательство TАПÌTh(ИП) было получено австрийским математиком К.Геделем в 1930 году. Теорема полноты ИП. Формула исчисления предикатов в том и только том случае является тавтологией, если она есть теорема ИП, т.е. выполняется равенство TАП=Th(ИП). Таким образом, ИП является адекватным инструментом получения логических законов. Теорема о непротиворечивости ИП. В исчислении предикатов невозможно доказать никакую формулу F вместе с ее отрицанием ØF. С другой стороны, английский математик А.Черч в 1936 году доказал следующий принципиально важный результат. Теорема о неразрешимость ИП. Не существует универсальной эффективной процедуры (алгоритма), которая для любой формулы определяет, является ли эта формула теоремой ИП. Таким образом, исчисление предикатов в отличие от исчисления высказываний является не только адекватным, но и безальтернативным инструментом получения логических законов. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 называется логически равносильными, если результат применения к ним логической операции эквивалентность
называется логически равносильными, если результат применения к ним логической операции эквивалентность  является тавтологией.
является тавтологией.  , или просто
, или просто  .
. означает, что
означает, что  .
. не содержит предметную переменную y и формула
не содержит предметную переменную y и формула  получается из
получается из  и
и  будут логически равносильны соответственно формулам
будут логически равносильны соответственно формулам  и
и  , т.е. выполняются равенства:
, т.е. выполняются равенства: и
и  .
. справедливы следующие утверждения:
справедливы следующие утверждения: ,
,  ,
, ,
,  .
. справедливы следующие утверждения:
справедливы следующие утверждения: ,
, .
. предметная переменная x не входит свободно, то справедливы также утверждения:
предметная переменная x не входит свободно, то справедливы также утверждения: ,
,  .
. предметная переменная x не входит свободно, то для любой формулы
предметная переменная x не входит свободно, то для любой формулы  справедливы следующие утверждения:
справедливы следующие утверждения: ,
,  .
. ,
,  .
. ,
, – некоторые кванторы и Y – формула без кванторов.
– некоторые кванторы и Y – формула без кванторов. , в которой все кванторы стоят в самом начале формулы и которая называется предваренной нормальной формой (сокращенно ПНФ) формулы
, в которой все кванторы стоят в самом начале формулы и которая называется предваренной нормальной формой (сокращенно ПНФ) формулы  ,
,  .
.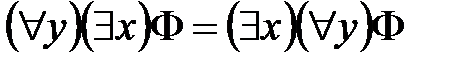
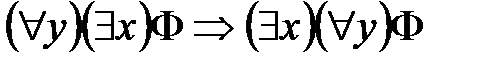
 алгебры предикатов называется логическим следствием формулы
алгебры предикатов называется логическим следствием формулы  , если
, если  , т.е. в любой интерпретации M формула
, т.е. в любой интерпретации M формула  , при которой выполняется формула
, при которой выполняется формула 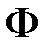 называется логическим следствием множества формул
называется логическим следствием множества формул  , если в любой интерпретации M формула
, если в любой интерпретации M формула  .
. и называется логическим следованием. При этом формулы из
и называется логическим следованием. При этом формулы из  .
.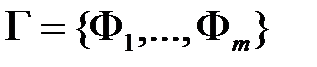 записывают
записывают  .
. .
. равносильно каждому из следующих условий:
равносильно каждому из следующих условий: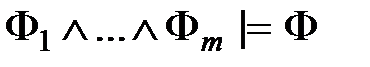 ,
, ,
, .
.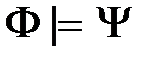 равносильно
равносильно 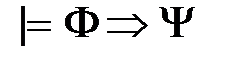 . Отсюда также следует, что
. Отсюда также следует, что 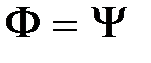 равносильно тому, что
равносильно тому, что  .
.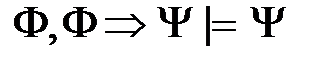 ;
; ;
;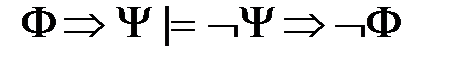 ;
;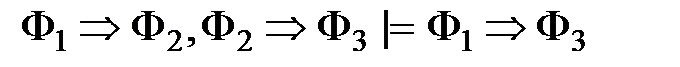 .
. ,
, ,
, ,
, – произвольные формулы исчисления высказываний.
– произвольные формулы исчисления высказываний. определяется по формуле MP
определяется по формуле MP  .
. .
. , в которой:
, в которой: =F ;
=F ; либо является аксиомой, либо получается из некоторых двух предыдущих формул
либо является аксиомой, либо получается из некоторых двух предыдущих формул  по правилу вывода MP.
по правилу вывода MP.  |-F для некоторого конечного числа элементов
|-F для некоторого конечного числа элементов 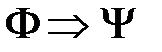 .
. . Индукцией по значениям
. Индукцией по значениям  докажем, что Γ |-
докажем, что Γ |-  .
. ,
, 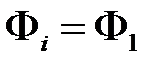 - либо является аксиомой, либо принадлежит множеству Γ, либо совпадает с формулой
- либо является аксиомой, либо принадлежит множеству Γ, либо совпадает с формулой  .
. формула
формула  - аксиома, то в первых двух случаях по правилу вывода MP получаем Γ |-
- аксиома, то в первых двух случаях по правилу вывода MP получаем Γ |-  .
. и докажем, что Γ |-
и докажем, что Γ |-  . По определению вывода формула
. По определению вывода формула  либо аксиома, либо принадлежит Γ, либо совпадает с формулой
либо аксиома, либо принадлежит Γ, либо совпадает с формулой  по правилу вывода MP.
по правилу вывода MP. имеет вид
имеет вид  . Тогда по предположению индукции из множества формул Γ выводятся формулы
. Тогда по предположению индукции из множества формул Γ выводятся формулы  ,
,  и по схеме
и по схеме  формула
формула  - аксиома. Дважды применяя правило вывода MP, получим вывод из множества Γ формулы
- аксиома. Дважды применяя правило вывода MP, получим вывод из множества Γ формулы  .
. , то, Γ |-
, то, Γ |-  .
. ;
; ;
; ;
; ;
; ;
; ;
;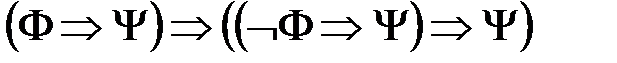 .
. , для которых задано некоторое распределение истинностных значений
, для которых задано некоторое распределение истинностных значений  . Тогда для значения
. Тогда для значения  выполняется условие:
выполняется условие: |-
|-  . (1)
. (1) и
и  .
. .
. и (1) имеет вид
и (1) имеет вид  |-
|-  .
. выполняется (1) и докажем, что это свойство для формулы Φ с числом вхождения пропозициональных связок n.
выполняется (1) и докажем, что это свойство для формулы Φ с числом вхождения пропозициональных связок n.  , то в формулу Ψ входит меньше n пропозициональных связок и по предположению индукции выполняется:
, то в формулу Ψ входит меньше n пропозициональных связок и по предположению индукции выполняется: .
. , то
, то  и, с другой стороны, в силу
и, с другой стороны, в силу 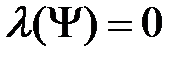 выполняется:
выполняется:  . Значит, для формулы Φ верно (1).
. Значит, для формулы Φ верно (1). , то
, то  . С другой стороны, в силу
. С другой стороны, в силу  выполняется:
выполняется:  и
и  , то по правилу вывода MP получаем:
, то по правилу вывода MP получаем: ,
, , то в формулы
, то в формулы  входит меньше n пропозициональных связок и по предположению индукции выполняется:
входит меньше n пропозициональных связок и по предположению индукции выполняется: (i=1,2).
(i=1,2). дает тавтологию Y;
дает тавтологию Y; для любых
для любых  .
. ,
,  |-
|- 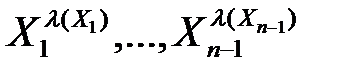 |-
|-  .
. ,
,  |-
|-  |-
|-  .
. .
. .
.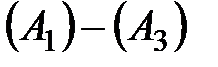 , в которых
, в которых 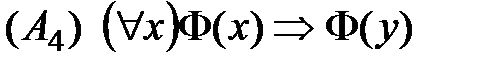
 в которую y не входит связно;
в которую y не входит связно;
 , что x в формулу
, что x в формулу  не входит свободно.
не входит свободно. .
. по одному из правил вывода MP или Gen. При этом
по одному из правил вывода MP или Gen. При этом