
|
|
Метод семантических таблицРассматривается интерпретация M формул языка УИП сигнатуры W. Семантической таблицей называется упорядоченная пара множеств формул
Семантическая таблица - -
Примеры. 1. Семантическая таблица
Выполнима для двухэлементной интерпретации. 2. Семантическая таблица
невыполнима. Теорема (о табличной проверке общезначимости формул). Для любой формулы F языка УИП сигнатуры W условие Семантическая таблица - закрытой, если - атомарной, если множества Предложение. Каждая закрытая семантическая таблица невыполнима и каждая незакрытая атомарная семантическая таблица выполнима. Следствие. Если для формулы F языка УИП сигнатуры W выполнимость семантической таблицы Правила корректного преобразования семантических таблиц, сохраняющие выполнимость этих таблиц, называются правилами табличного вывода. Для семантических таблиц
где в правилах и в правилах Лемма (корректность основных правил табличного вывода). Для всех основных правил табличного вывода вида Табличным выводом для семантической таблицы Табличный вывод называется успешным, если он является конечным деревом, все листья которого являются закрытыми таблицами. Теорема полноты табличного вывода. Семантическая таблица Следствие. Формула F языка УИП сигнатуры W общезначима в том и только том случае, если для семантической таблицы Автоматическое доказательство теорем В исчислении предикатов (сокращенно, ИП) с помощью понятия вывода формул определяется множество Th(ИП) всех теорем ИП, которое в силу теоремы полноты совпадает с множеством общезначимых формул ИП. Из неразрешимости ИП следует, что не существует универсальной эффективной процедуры (алгоритма), которая для любой формулы определяет, является ли эта формула теоремой ИП. Тем не менее, существуют алгоритмы поиска доказательства, которые для общезначимых формул подтверждают, что эти формулы общезначимы, и для необщезначимых формул в общем случае не заканчивают свою работу. Автоматические системы построения доказательств называют пруверами и предъявляют им следующие требования: 1) корректность, 2) полнота, 3) эффективность. Примером такого алгоритма является метод семантических таблиц, который: 1) корректен, 2) полон, 3) но малоэффективен, так как использует двойной переборный поиск: · выбор формулы, к которой применяется правило вывода, · выбор правила, которое нужно применять к формуле (и которое предполагает практически невозможный перебор всех термов). Поэтому необходим способ быстрого и точного вычисления тех термов, которые необходимо подставлять в формулы вместо переменных, связанных кванторами. Альтернативную систему автоматического поиска доказательства разработали Жак Эрбран, Дж.Робинсон и др. на основе алгоритма нахождения интерпретации, опровергающей рассматриваемую формулу. Так как для общезначимых формул опровергающих интерпретаций нет, то такой алгоритм заканчивает работу за конечное число шагов. Первым шагом алгоритма Эрбрана является приведение рассматриваемой формулы к специальным нормальным формам, которые аналогичны ДНФ и КНФ для формул исчисления высказываний (сокращенно, ИВ). 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
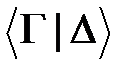 , где
, где  – множество истинных для рассматриваемой интерпретации M формул и
– множество истинных для рассматриваемой интерпретации M формул и  – множество ложных для рассматриваемой интерпретации M формул.
– множество ложных для рассматриваемой интерпретации M формул.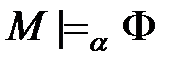 для любой формулы
для любой формулы 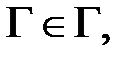
 для любой формулы
для любой формулы 
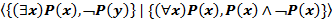
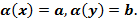
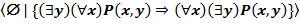
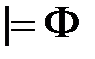 выполняется тогда и только тогда, когда семантическая таблица
выполняется тогда и только тогда, когда семантическая таблица  невыполнима.
невыполнима.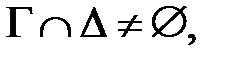
 состоят из атомарных формул.
состоят из атомарных формул. сводится к выполнимости некоторой закрытой семантической таблицы, то формула F общезначима.
сводится к выполнимости некоторой закрытой семантической таблицы, то формула F общезначима. такие правила символически записываются выражениями вида
такие правила символически записываются выражениями вида 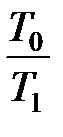 или
или 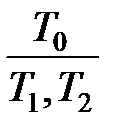 , которые означают, что таблица
, которые означают, что таблица  выполнима в том и только том случае, если выполнима таблица
выполнима в том и только том случае, если выполнима таблица  (или, соответственно, одна из таблиц
(или, соответственно, одна из таблиц 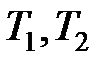 ). Основные правила табличного вывода
). Основные правила табличного вывода


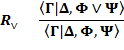
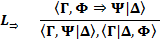
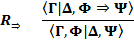


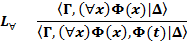

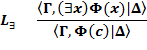

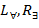 формула F(t) – результат замены всех вхождений переменной x в формулу F(x) термом t, переменные которого не попадают в формуле
формула F(t) – результат замены всех вхождений переменной x в формулу F(x) термом t, переменные которого не попадают в формуле 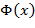 в области действия кванторов по этим переменным,
в области действия кванторов по этим переменным,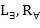 формула F(c) – результат замены всех вхождений переменной x в формулу F(x) постоянным символом c, которыйне содержится ни в формуле
формула F(c) – результат замены всех вхождений переменной x в формулу F(x) постоянным символом c, которыйне содержится ни в формуле 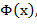 ни в формулах из множеств
ни в формулах из множеств 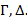
 выполнима в том и только том случае, если выполнима таблица
выполнима в том и только том случае, если выполнима таблица 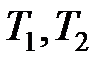 ).
). в вершину
в вершину 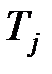 (и в вершину
(и в вершину 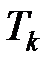 ) идет дуга в том и только том случае, если
) идет дуга в том и только том случае, если 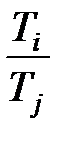 или
или  являются правилами табличного вывода. При этом листьями такого дерева являются закрытые или атомарные таблицы.
являются правилами табличного вывода. При этом листьями такого дерева являются закрытые или атомарные таблицы.