
|
|
Аксиоматические теории первого порядкаПри исследовании конкретной математической теории фиксируют некоторые наборы исходных предикатных символов Множество Принципиальное отличие УИП от ИП заключается в следующем. 1. Алфавит УИП состоит из предметных переменных, логических и вспомогательных символов, а также некоторых исходных предикатных символов В результате элементы области интерпретации такого языка будут описываться не только с помощью предметных переменных, но и с помощью так называемых термов – специальных выражений языка, которые индуктивно определяются следующим образом: а) все предметные переменные и предметные символы являются термами, б) если f – сигнатурный n-арный функциональный символ и 2. Формулы УИП определяются по аналогии с формулами ИП за исключением исходного шага индукции – определения атомарных формул, которые в данном случае имеют вид выражений Записывают Формула без свободных вхождений переменных называется замкнутой формулой или предложением. 3. Множество аксиом УИП описывается пятью определенными в предыдущем разделе схемами аксиом 4. Правилами вывода УИП являются правило modus ponens (MP) и правило обобщения (Gen). 5. Формула F называется теоремой УИП, если найдется такая конечная последовательность формул Последовательность формул Вывод формулы F сокращенно обозначают символом |-F и говорят, что «F есть теорема». Множество всех таких теорем обозначается символом ThW(S) и называется элементарной теорией (или теорией первого порядка) узкого исчисления предикатов сигнатуры W с множеством аксиом S. Принципиальное отличие интерпретации формул языка УИП от описанной ранее интерпретации формул алгебры предикатов заключается в том, что определение истинности формул УИП сигнатуры W вводится с помощью интерпретации этого языка в конкретных алгебраических системах с первоначально фиксированными предикатными, функциональными и предметными символами сигнатуры W. Для придания содержательного смысла формулам УИП сигнатуры W сначала задается область интерпретации – непустое множество M, которое является областью возможных значений всех предметных переменных, и затем на этом множестве M для каждого символа сигнатуры В результате получается алгебраическая система с основным множеством M, которая называется алгебраической W-системой и обозначается Конкретные значения предметным переменным по-прежнему присваиваются с помощью оценок предметных переменных, т.е. отображений a таких переменных в область интерпретации M. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
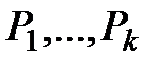 соответствующей арности
соответствующей арности  , исходных функциональных символов
, исходных функциональных символов  соответствующей арности
соответствующей арности 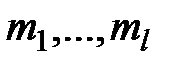 и исходных предметных символов
и исходных предметных символов  .
. называется алгебраическим типом или сигнатурой математической теории.
называется алгебраическим типом или сигнатурой математической теории. – термы, то выражение
– термы, то выражение  является термом.
является термом.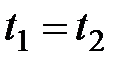 ,
,  для любых термов
для любых термов  и сигнатурных n-арных предикатных символов P.
и сигнатурных n-арных предикатных символов P. , если в формулу F входят предметные переменные
, если в формулу F входят предметные переменные  .
. , в которых
, в которых  теперь являются произвольными формулами УИП, и дополнительной системой формул S специальных аксиом рассматриваемой математической теории. Аксиомы первого вида называются логическими и аксиомы второго вида – нелогическими аксиомами УИП.
теперь являются произвольными формулами УИП, и дополнительной системой формул S специальных аксиом рассматриваемой математической теории. Аксиомы первого вида называются логическими и аксиомы второго вида – нелогическими аксиомами УИП. , в которой
, в которой  =F и каждая формула
=F и каждая формула  либо является логической аксиомой из схем
либо является логической аксиомой из схем  по одному из правил вывода MP или Gen.
по одному из правил вывода MP или Gen.  фиксируется соответствующий математический объект: для каждого предикатного символа
фиксируется соответствующий математический объект: для каждого предикатного символа 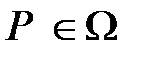 арности
арности  фиксируется
фиксируется 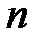 -арное отношение
-арное отношение  на множестве M, для каждого функционального символа
на множестве M, для каждого функционального символа 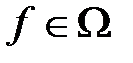 арности
арности  фиксируется
фиксируется 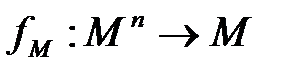 на множестве M и для каждого предметного символа
на множестве M и для каждого предметного символа  фиксируется элемент
фиксируется элемент  в множестве M.
в множестве M. или просто
или просто  . Такая система называется также интерпретацией языка УИП сигнатуры W.
. Такая система называется также интерпретацией языка УИП сигнатуры W.