
|
|
Интерпретация теории первого порядкаДля придания содержательного смысла формулам УИП сигнатуры W сначала задается область интерпретации – непустое множество M, которое является областью возможных значений всех предметных переменных, и затем на этом множестве M для каждого символа сигнатуры В результате получается алгебраическая система с основным множеством M, которая называется алгебраической W-системой и обозначается Конкретные значения предметным переменным по-прежнему присваиваются с помощью оценок предметных переменных, т.е. отображений a таких переменных в область интерпретации M. Выполнимость формул теории первого порядка Выполнимость формулы 1) при оценке 2) если 3) если Определение. Винтерпретации M формула F называется: - общезначимой (или тождественно истинной) и записывается - выполнимой, если - опровержимой, если для некоторой оценки - тождественно ложной, если для любой оценки Определение. Интерпретация M языка УИП сигнатуры W называется моделью множества формул S, если в этой интерпретации M тождественно истинны все формулы Определение. Формула F называется общезначимой формулой узкого исчисления предикатов сигнатуры W с множеством аксиом S, если она тождественно истинна в любой моделимножества формул S. Множество всех таких общезначимых формул обозначим TW(S). Главная цель - определение такой системы нелогических аксиом S, для которой ThW(S)=TW(S). Примеры теорий первого порядка 1. Теория полугрупп. Пусть сигнатура Рассмотрим систему аксиом S: Моделями множества формул S языка УИП сигнатуры Примеры полугрупп дают основные числовые множества с операциями сложения или умножения, а также множества всех преобразований любого непустого множества с операцией композиции. Элементарная теория ThW(S) называется теорией полугрупп. 2. Теория групп. Пусть
Моделями множества формул S языка УИП сигнатуры Пример группы дает множество целых чисел с операцией сложения и выделенным элементом 0, а также множество всех перестановок любого непустого множества с операцией композиции и выделенной тождественной перестановкой. Элементарная теория ThW(S) называется теорией групп. Если к системе аксиом S добавить еще одну формулу 3. Теория упорядоченных множеств. Пусть сигнатура Система аксиом S:
В этом случае моделями множества формул S языка УИП сигнатуры Элементарная теория ThW(S) называется теорией упорядоченных множеств. Если к системе аксиом S добавить еще одну формулу 4. Теория вещественных чисел. Пусть сигнатура
где В этом случае элементарная теория ThW(S) называется теорией вещественных чисел. Моделью такой теории является, например, множество вещественных чисел R с отношением £ сравнения чисел по величине, бинарными операциями сложения + и умножения × чисел, выделенными числами 0 и 1. Такая модель R=(R;£,+,×,0,1) называется стандартной моделью теории вещественных чисел. С другой стороны, известно, что эта теория имеет также модели, которые существенно отличаются от стандартной модели R и которые называются нестандартными моделями теории вещественных чисел. Показательно, что, если последнюю аксиому теории вещественных чисел переформулировать, заменив формулу УИП Но эта аксиоматика уже не является элементарной. 5. Теория арифметики. Сигнатура Система аксиом S: где Элементарная теория ThW(S) называется теорией арифметики и обозначается Ar. Моделью такой теории является, например, множество неотрицательных целых чисел N0 с бинарными операциями сложения + и умножения × чисел, унарной операцией С другой стороны, известно, что теория Ar имеет также модели, которые существенно отличаются от стандартной модели N0 и которые называются нестандартными моделями теории арифметики. Отметим, что теория Arпринято называть также арифметикой Пеано в честь итальянского математика Дж.Пеано, который в 1891 году впервые рассмотрел аксиоматику множества натуральных чисел. Эта аксиоматикапринципиально отличалась от описанной выше системы только последней аксиомой, которая Дж.Пеано была сформулирована в форме следующего принципа математической индукции: если Показательно, что, с одной стороны, аксиоматика Пеано имеет единственную модель – множество натуральных чисел N0=(N0;+,×,S,0), но, с другой стороны, последняя аксиома Пеано не может быть выражена на языке УИП рассматриваемой сигнатуры Более того, известная теорема Геделя о неполноте формальной арифметики показывает, что множество всех формул языка УИП сигнатуры 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 фиксируется соответствующий математический объект: для каждого предикатного символа
фиксируется соответствующий математический объект: для каждого предикатного символа 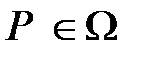 арности
арности  фиксируется
фиксируется  -арное отношение
-арное отношение  на множестве M, для каждого функционального символа
на множестве M, для каждого функционального символа 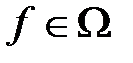 арности
арности  фиксируется
фиксируется 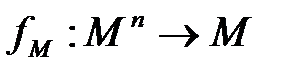 на множестве M и для каждого предметного символа
на множестве M и для каждого предметного символа  фиксируется элемент
фиксируется элемент  в множестве M.
в множестве M. или просто
или просто  . Такая система называется также интерпретацией языка УИП сигнатуры W.
. Такая система называется также интерпретацией языка УИП сигнатуры W.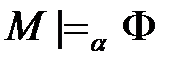 :
: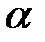 каждый терм
каждый терм  интерпретируется в
интерпретируется в  , который получается в результате вычисления для элементов
, который получается в результате вычисления для элементов  значений соответствующих сигнатурных операций, с помощью которых определяется терм
значений соответствующих сигнатурных операций, с помощью которых определяется терм  ;
; - атомарная формула
- атомарная формула 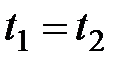 для термов
для термов  , то
, то  равносильно
равносильно  ;
; для n-местного предикатного символа
для n-местного предикатного символа  и термов
и термов 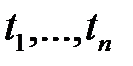 , то
, то  равносильно тому, что
равносильно тому, что  истинно;
истинно;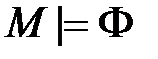 ,если
,если  при любых оценках
при любых оценках  ;
; для некоторой оценки
для некоторой оценки  ;
; неверно, что
неверно, что  ;
;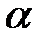 неверно, что
неверно, что 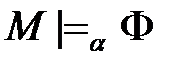 .
. .
. содержит один бинарный функциональный символ
содержит один бинарный функциональный символ 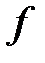 , для которого используется инфиксная запись с помощью символа × : для любых предметных переменных x,y терм
, для которого используется инфиксная запись с помощью символа × : для любых предметных переменных x,y терм  обозначается
обозначается  , или просто
, или просто 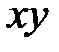 . Тогда термамы сигнатуры
. Тогда термамы сигнатуры  :
: 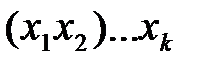 и атомарные формулы:
и атомарные формулы:  (для некоторых
(для некоторых  и правильно расставленных скобок).
и правильно расставленных скобок).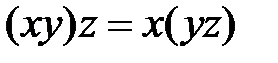 , выражающую свойство ассоциативности операции умножения.
, выражающую свойство ассоциативности операции умножения. содержит один бинарный функциональный символ × (для которого используется прежняя инфиксная запись) и один предметный символ e. Рассмотрим систему аксиом S:
содержит один бинарный функциональный символ × (для которого используется прежняя инфиксная запись) и один предметный символ e. Рассмотрим систему аксиом S: ,
,  .
. , то моделями полученного множества формул
, то моделями полученного множества формул  будут коммутативные группы. Поэтому элементарная теория ThW(
будут коммутативные группы. Поэтому элементарная теория ThW(  ) называется теорией коммутативных групп.
) называется теорией коммутативных групп. содержит один бинарный предикатный символ
содержит один бинарный предикатный символ  , для которого используется инфиксная запись с помощью символа £ : формула
, для которого используется инфиксная запись с помощью символа £ : формула  обозначается
обозначается  .
. ,
,  ,
,  .
. , то моделями полученного множества формул
, то моделями полученного множества формул  содержит один бинарный предикатный символ £, два бинарных функциональных символа +, × (для которых используется инфиксная запись) и два предметных символа 0,1. Рассмотрим систему аксиом S:
содержит один бинарный предикатный символ £, два бинарных функциональных символа +, × (для которых используется инфиксная запись) и два предметных символа 0,1. Рассмотрим систему аксиом S: ,
,  ,
, ,
,  ,
, ,
,  ,
,  ,
,  ,
,  ,
,  ,
,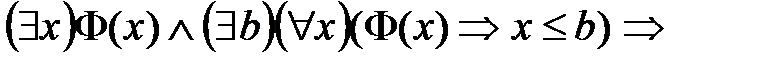

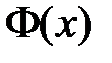 – произвольная формула языка УИП рассматриваемой сигнатуры
– произвольная формула языка УИП рассматриваемой сигнатуры  на неэлементарную формулу
на неэлементарную формулу  для одноместной предикатной переменной X, то полученная система аксиом будет иметь единственную модель – систему вещественных чисел R=(R;£,+,×,0,1).
для одноместной предикатной переменной X, то полученная система аксиом будет иметь единственную модель – систему вещественных чисел R=(R;£,+,×,0,1).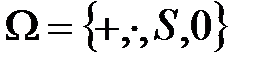 содержит два бинарных функциональных символа +, × (для которых используется инфиксная запись), один унарных функциональный символ S и один предметный символ 0.
содержит два бинарных функциональных символа +, × (для которых используется инфиксная запись), один унарных функциональный символ S и один предметный символ 0. ,
, 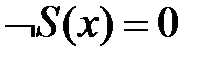 ,
,  ,
,  ,
,  ,
,  ,
,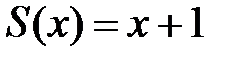 и выделенным числом 0. Такая модель N0=(N0;+,×,S,0) называется стандартной моделью арифметики.
и выделенным числом 0. Такая модель N0=(N0;+,×,S,0) называется стандартной моделью арифметики. – такое свойство натуральных чисел, что
– такое свойство натуральных чисел, что  (т.е. 0 обладает этим свойством
(т.е. 0 обладает этим свойством  ) и
) и  (т.е. вместе с любым натуральным числом n этим свойством
(т.е. вместе с любым натуральным числом n этим свойством  обладает следующее за ним число n+1), то данным свойством
обладает следующее за ним число n+1), то данным свойством