
|
|
Нормальные формы для формул алгебры предикатовФормула исчисления предикатов Φ находится в пренексной (соответственно, предклазуальной) нормальной форме (сокращенно ПНФ и ПкНФ), если она имеет вид
где
Теорема 1. Любая формула исчисления предикатов Такая формула Пусть замкнутая формула исчисления предикатов Φ находится в ПкНФ:
где В частности, если первый квантор Предположим, что r>1. Тогда с помощью обозначения
формула Φ представляется в виде:
где Тогда выполнимость формулы Φ в интерпретации M равносильна выполнимости в интерпретации M формулы
с соответствующей интерпретацией в M нового функционального символа f арности r-1. В случае r=1 формула Аналогичным образом в кванторной приставке формуле Φ можно удалить любой квантор существования 1) если левее квантора существования 2) если же левее квантора существования
для значений В результате такой замены всех кванторов существования в формуле Φ получим замкнутую ПкНФ При этом формула Φ выполнима или противоречива одновременно с формулой Рассмотренный прием удаления квантора существования был введен Скулемом и называется скулемизацией формул. Вводимые в процессе скулемизации новые функциональные и предметные символы называются функторами Скулема или скулемовскими функциями. Полученную в результате скулемизации замкнутую ПкНФ Теорема 1. Любая замкнутая формула исчисления предикатов При этом формула Φ выполнима или противоречива одновременно с ее КлНФ. Пример. Как показано в предыдущем примере, замкнутая формула
имеет ПкНФ
результатом скулемизации которой является формула
с новым предметным символом c. Значит, Метод Эрбрана По предыдущей теореме противоречивость замкнутой формулы исчисления предикатов Φ равносильна противоречивости ее скулемовской стандартной формы
с конъюнктивным ядром С другой стороны, по теореме полноты, формула Так как кванторы общности проносятся через конъюнкции, то формула
= и, значит, ее невыполнимость равносильна невыполнимости множества универсальных замыканий
формул из множества дизъюнктов Невозможно рассмотреть все интерпретации множества формул S на всех областях интерпретации, так как множество таких областей интерпретации бесконечно. Однако Эрбран показал, что при доказательстве невыполнимости такого множества формул S можно ограничиться рассмотрением интерпретаций в одной специальной области интерпретации, которая называется эрбрановским универсумом. Пусть На первом шаге индукции для множества S определяется множество констант нулевого уровня H0 по правилу:
Затем для каждого натурального значения
где Объединение всех множеств Hi Примеры. 1. Для множества дизъюнктов
эрбрановский универсум
2. Для множества дизъюнктов
эрбрановский универсум
На множестве для каждого n-арного функционального символа f из множества
Интерпретацией каждого n-арного предикатного символа P, встречающегося в формулах множества S является некоторое n-арное отношение Символически такие отношения могут быть заданы перечислением атомарных формул:
Множество всех атомарных формул с термами из Базис B является счетным множеством:
Интерпретация bP предикатных символов из формул множества S естественно задается в виде множества литер:
где Интерпретации b множества формул S в 1) для каждого предметного символа c, встречающегося в формулах множества S, выполняется равенство: 2) для каждого n-арного функционального символа f , встречающегося в формулах множества S, соответствующая n-арная операция 3) для некоторого наперед заданного множества литер
Пример. Для множества дизъюнктов
эрбрановский универсум имеет вид:
Значит, эрбрановский базис имеет вид:
Теорема. Множество дизъюнктов S невыполнимо в том и только том случае, если множество S ложно при всех его H-интерпретациях. Таким образом, при доказательстве невыполнимости множества дизъюнктов S можно ограничиться рассмотрением его H-интерпретаций. Такой подход позволяет свести вопрос об общезначимости рассматриваемой формулы исчисления предикатов Φ к вопросу об общезначимости бескванторных формул D, который в свою очередь легко сводится к вопросу об общезначимости формул исчисления высказываний заменой всех атомарных формул, входящих в формулу D, пропозициональными переменными. Теорема Эрбрана. Пусть

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
, – некоторые кванторы и Y – бескванторная формула, находящейся в ДНФ (соответственно, КНФ). При этом последовательность кванторов
– некоторые кванторы и Y – бескванторная формула, находящейся в ДНФ (соответственно, КНФ). При этом последовательность кванторов 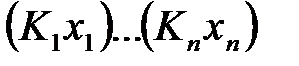 называется кванторной приставкой и формула Y называется дизъюнктивным (соответственно, конъюнктивным) ядром формулы Φ.
называется кванторной приставкой и формула Y называется дизъюнктивным (соответственно, конъюнктивным) ядром формулы Φ.  логически эквивалентна формуле
логически эквивалентна формуле  , находящейся в ПНФ (соответственно, ПкНФ).
, находящейся в ПНФ (соответственно, ПкНФ). называется пренексной нормальной формой (сокращенно ПНФ) формулы
называется пренексной нормальной формой (сокращенно ПНФ) формулы  ,
, – конъюнктивное ядроформулы Φ, т.е. бескванторная формула со свободными переменными
– конъюнктивное ядроформулы Φ, т.е. бескванторная формула со свободными переменными  , находящаяся в КНФ. Пусть квантор
, находящаяся в КНФ. Пусть квантор  для некоторого
для некоторого  являетсяпервым в формулеΦ квантором существования.
являетсяпервым в формулеΦ квантором существования. являетсяквантором существования, то в формулеΦ нет предшествующих ему кванторов общности.
являетсяквантором существования, то в формулеΦ нет предшествующих ему кванторов общности.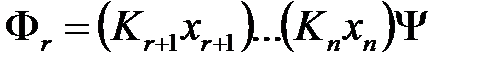
 ,
, – формуласо свободными переменными
– формуласо свободными переменными  .
.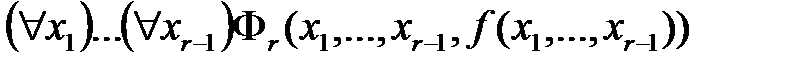
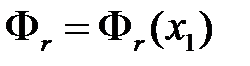 можетзависеть только от свободной переменной
можетзависеть только от свободной переменной  и выполнимость формулы Φ в интерпретации M равносильна выполнимости в интерпретации M формулы
и выполнимость формулы Φ в интерпретации M равносильна выполнимости в интерпретации M формулы  с соответствующей интерпретацией в M нового предметного символа c.
с соответствующей интерпретацией в M нового предметного символа c. для
для 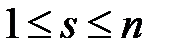 по следующему правилу:
по следующему правилу: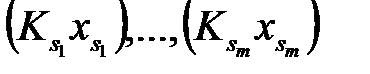
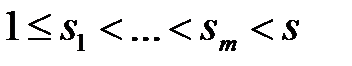 , то выбираем новый m-арный функциональный символ f, заменяем все вхождения переменной xs в конъюнктивное ядроформулы Φ выражением
, то выбираем новый m-арный функциональный символ f, заменяем все вхождения переменной xs в конъюнктивное ядроформулы Φ выражением 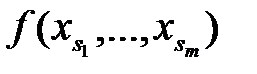 и вычеркиваем
и вычеркиваем  ,кванторная приставка которой получается из кванторной приставки формулы Φ удалением всех кванторов существованияи которая содержит новые символы – функциональные или предметные.
,кванторная приставка которой получается из кванторной приставки формулы Φ удалением всех кванторов существованияи которая содержит новые символы – функциональные или предметные.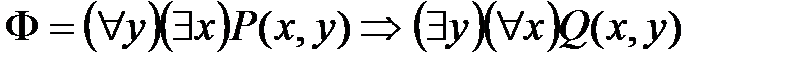
 ,
,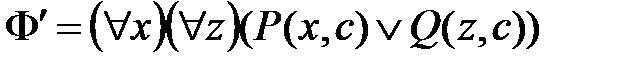
 является КлНФ формулы
является КлНФ формулы 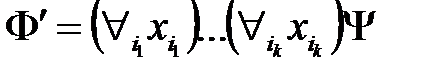
 ,где
,где  –некоторые дизъюнкты исчисления предикатов.
–некоторые дизъюнкты исчисления предикатов.
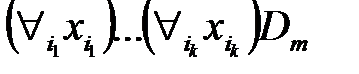

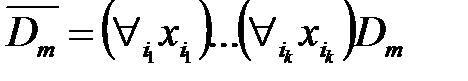
 .
. – множество всех предметных символов и
– множество всех предметных символов и  – множество всех функциональных символов, встречающихся в формулах множества S.
– множество всех функциональных символов, встречающихся в формулах множества S.  , если
, если 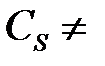 Æ, и
Æ, и  для одного нового постоянного символа a, если
для одного нового постоянного символа a, если  Æ.
Æ.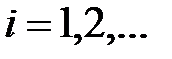 определяется множество констант i-го уровня Hi как множество всех выражений вида
определяется множество констант i-го уровня Hi как множество всех выражений вида ,
, и f – n-арный функциональный символ из множества
и f – n-арный функциональный символ из множества 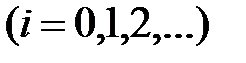 называется эрбрановским универсумом множества S и обозначается
называется эрбрановским универсумом множества S и обозначается  .
.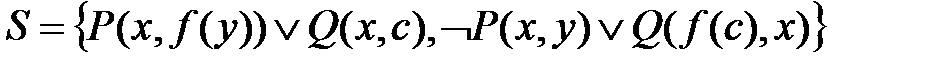
 .
.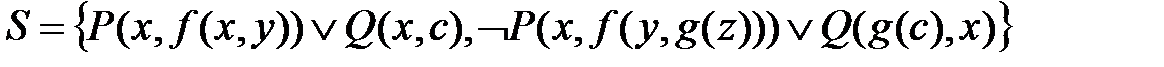
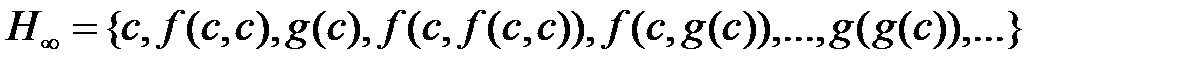
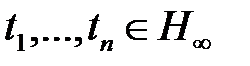 значение
значение 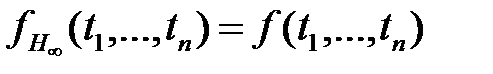 – есть терм из множества
– есть терм из множества  на эрбрановском универсуме
на эрбрановском универсуме  .
. .
. ,
, , если атомарная формула
, если атомарная формула  истинна в интерпретации b, и
истинна в интерпретации b, и  , если атомарная формула
, если атомарная формула 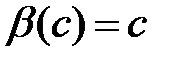 ;
; на множестве
на множестве  интерпретация
интерпретация  каждого n-арного предикатного символа P, встречающегося в формулах множества S, определяется как n-арное отношение
каждого n-арного предикатного символа P, встречающегося в формулах множества S, определяется как n-арное отношение  на множестве
на множестве 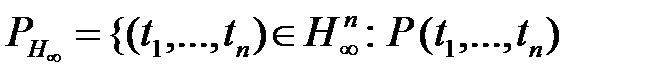 – элемент
– элемент  .
.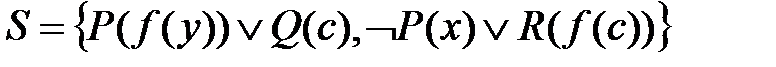
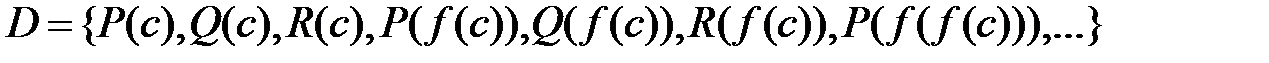 .
.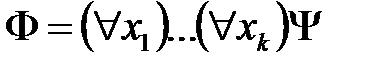 – замкнутая формула с конъюнктивным ядром
– замкнутая формула с конъюнктивным ядром  и
и  . Тогда формула Φ невыполнима в том и только том случае, если для некоторого конечного набора термов
. Тогда формула Φ невыполнима в том и только том случае, если для некоторого конечного набора термов 
 невыполнима конъюнкция формул
невыполнима конъюнкция формул