
|
|
Минимизация булевых многочленовРассмотрим вопрос минимизации ДНФ p . Конъюнкт q называется импликантом формы p, если Лемма 1. Любая ДНФ p эквивалентна некоторой сокращенной ДНФ. Сокращенную ДНФ формы p можно получить методом Квайна с помощью последовательного применения следующих двух видов операций: 1) операция склеивания, которая для конъюнктов q и булевых переменных x определяется по формуле:
2) операция поглощения, которая для конъюнктов q, булевых переменных x и значений
В общем случае сокращенная ДНФ формы p не является минимальной формой, так как она может содержать лишние импликанты, удаление которых не изменяет булеву функцию Тупиковые ДНФ с наименьшим числом вхождений в них булевых переменныхназываются минимальными ДНФ. Лемма 2. Любая ДНФ p эквивалентна некоторой минимальной ДНФ.
Минимальная ДНФ формы p получается с помощью матрицы Квайна: - столбцы матрицы помечаются конъюнктами - строки матрицы помечаются импликантами - на пересечении строки Тупиковые ДНФ - дизъюнкции тех минимальных наборов импликант, в строках которых имеются звездочки для всех столбцов матрицы Квайна. Тупиковые ДНФ с наименьшим числом вхождений булевых переменных являются искомыми минимальными ДНФ формы p . Следствие 3. Любая булева функция, не равная тождественно нулю, представима минимальной ДНФ и любая булева функция, не равная тождественно единице, представима минимальной КНФ. Логика предикатов Понятие предиката Определение. Предикатом называется утверждение, содержащее переменные Обозначаются предикаты Переменные Более точно, предикат P с n предметными переменными называется n-арным или n-местным предикатом и обозначается Предикат Если отвлечься от содержания высказываний и учитывать только их истинностные значения, то предикат можно рассматривать как функцию со значениями в множестве Рассматривая такую функцию на некотором фиксированном множестве M допустимых значений предметных переменных предиката, получим n-арное отношение на множестве M, состоящее из всех таких упорядоченных наборов Такое n-арное отношение обозначается символом P+ и называется множеством истинности предиката P на множестве M. Определение. Предикат - тождественно истинным, если для любых значений - тождественно ложным, если для любых значений - выполнимым, если для некоторых значений - опровержимым, если для некоторых значений Определение. Пусть предикаты одинаковой арности - предикаты - предикат
Алгебра предикатов Высказывания являются утверждениями без предметных переменных, их можно рассматривать как 0-местные предикаты. Значит, множество всех высказываний содержится в множестве всех предикатов и рассмотренные выше логические операции Отрицание n-местного предиката Конъюнкция n-местных предикатов Для любого множества M допустимых значений предметных переменных предикатов множества истинности предикатов взаимосвязаны с логическими операциями по следующим формулам:
Для предикатов определены принципиально новые унарные операции – операции квантификации, или операции действия на предметные переменные кванторами. Для каждой предметной переменной x рассматриваются два вида кванторов: Определение. Результатом действия квантора общности Определение. Результатом действия квантора существования Определение. Результатом действия квантора общности Определение. Результатом действия квантора существования
Результат действия такого квантора на предикат Ограниченный квантор существования
Результат действия такого квантора на предикат Ограниченный квантор общности
Результат действия такого квантора на предикат Определение. Алгеброй предикатов называется множество всех предикатов P с логическими операциями 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Импликанты, минимальные по числу вхождений в них булевых переменных, называются простыми импликантами. Дизъюнкция всех простых импликант формы p называется сокращенной ДНФ.
. Импликанты, минимальные по числу вхождений в них булевых переменных, называются простыми импликантами. Дизъюнкция всех простых импликант формы p называется сокращенной ДНФ. ;
; определяется по формуле:
определяется по формуле: .
.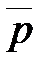 . В результате удаления таких лишних импликант получаются тупиковые ДНФ.
. В результате удаления таких лишних импликант получаются тупиковые ДНФ. формы p ;
формы p ; сокращенной ДНФ формы p ;
сокращенной ДНФ формы p ; и столбца
и столбца  ставится символ *, если импликант
ставится символ *, если импликант  является частью конъюнкта
является частью конъюнкта  .
.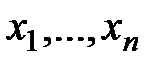 , которое превращается в высказывание при замене этих переменных конкретными объектами из некоторой области возможных значений.
, которое превращается в высказывание при замене этих переменных конкретными объектами из некоторой области возможных значений.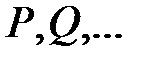
 .
. его n предметных переменных
его n предметных переменных  , имеющее определенное истинностное значение
, имеющее определенное истинностное значение  .
. .
. n элементов
n элементов  , для которых
, для которых  высказывание
высказывание  рассматриваются на множестве M. Тогда:
рассматриваются на множестве M. Тогда: и
и  называются эквивалентными, если P+ = Q+, т.е. при любых значениях
называются эквивалентными, если P+ = Q+, т.е. при любых значениях  ;
;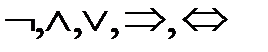 над высказываниями можно естественно продолжить на предикаты.
над высказываниями можно естественно продолжить на предикаты. , который при подстановке значений
, который при подстановке значений  , являющееся отрицанием высказывания
, являющееся отрицанием высказывания  определяется как n-местный предикат
определяется как n-местный предикат  , который при подстановке значений
, который при подстановке значений  , являющееся конъюнкцией высказываний
, являющееся конъюнкцией высказываний  .
. ,
,  ,
, ,
,  ,
, .
. – квантор общности по переменной x (читается «для всех x») и
– квантор общности по переменной x (читается «для всех x») и  – квантор существования по переменной x (читается «существует x»).
– квантор существования по переменной x (читается «существует x»). называется высказывание
называется высказывание 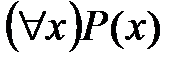 , которое истинно на множестве M допустимых значений переменной x в том и только том случае, если предикат
, которое истинно на множестве M допустимых значений переменной x в том и только том случае, если предикат  , которое истинно на множестве M допустимых значений переменной x в том и только том случае, если предикат
, которое истинно на множестве M допустимых значений переменной x в том и только том случае, если предикат  по переменной x1на n-местный предикат
по переменной x1на n-местный предикат  , который зависит от переменных
, который зависит от переменных  и который при значениях
и который при значениях  в том и только том случае истинен на множестве M допустимых значений переменной x1, если при любых значениях
в том и только том случае истинен на множестве M допустимых значений переменной x1, если при любых значениях 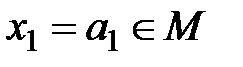 высказывание
высказывание  истинно.
истинно. по переменной x1на n-местный предикат
по переменной x1на n-местный предикат  , который зависит от переменных
, который зависит от переменных  высказывание
высказывание  истинно.Квантор существования и единственности
истинно.Квантор существования и единственности  определяется как сокращение записи следующей формулы
определяется как сокращение записи следующей формулы .
. обозначается
обозначается  и читается «существует и единственен x, для котороговыполняется
и читается «существует и единственен x, для котороговыполняется  »).
»).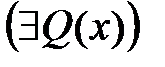 определяется как сокращение записи следующей формулы
определяется как сокращение записи следующей формулы .
. и и читается «существует x, удовлетворяющий
и и читается «существует x, удовлетворяющий  , для котороговыполняется
, для котороговыполняется  определяется как сокращение записи следующей формулы
определяется как сокращение записи следующей формулы .
. и читается «для всех x, удовлетворяющих
и читается «для всех x, удовлетворяющих  , выполняется
, выполняется