
|
|
Нормальные формы формул алгебры высказываний.Логика высказываний. Высказывание - повествовательное предложение, о котором можно судить, истинное оно или ложное. Обозначаются высказывания A,B,C,… Истинностное значение высказывания A обозначается символом l(A) и определяется по формуле: l(A)=1, если высказывание A истинно, и l(A)=0, если A ложно. Определение. Алгеброй высказываний называется множество всех высказываний P с логическими операциями Свойства алгебры высказываний P описываются с помощью формул, которые строятся из переменных символов с помощью знаков логических операций. Такие формулы приято называть также пропозициональными формулами Cимволы логических операций Переменные символы X,Y,Z,…, которые используются для обозначения высказываний и которые называются пропозициональными переменными. Определение. Формулы алгебры высказываний индуктивно определяются по правилам: 1) каждая пропозициональная переменная является формулой, 2) если F,Y – формулы, то формулами являются также выражения ( Множество всех формул алгебры высказываний обозначим FАВ . Если в формулу F входят переменные Из индуктивного определения формул следует, что если в формулу F вместо переменных Истинностное значение высказывания Определение. Формула - тавтологией (или тождественно истинной формулой) и обозначается - противоречием (или тождественно ложной формулой), если ее истинностная функция тождественно равна 0; - выполнимой, если ее истинностная функция не равна тождественно 0; - опровержимой, если ее истинностная функция не равна тождественно 1. - Тавтологии являются общими схемами построения истинных высказываний и в этом смысле выражают некоторые логические законы. - Примеры таких законов являются: - - - - Новые тавтологии можно получить с помощью следующих правил. -Правило отделения: если - Правило подстановки: если Логическая равносильность формул. Определение. Формулы Для обозначения логически эквивалентных формул используется символическая запись Такие выражения называются логическими эквивалентностями или просто равенствами формул. Лемма. Справедливы следующие равенства формул: 1) 2) 3) 4) 5) 6) 7) 8) 9) Лемма (Правило замены). Если формулы Это правило означает, что при замене в любой формуле Такие переходы называются равносильными преобразованиями формул. Нормальные формы формул алгебры высказываний. Отношение равносильности Из лемм следует, что для каждой формулы Определение.Литерой называется пропозициональная переменная X или ее отрицание ØX . Для обозначения литеры используется символ Xa, где aÎ{0,1} и по определению Определение.Конъюнктом (соответственно, дизъюнктом) называется литера или конъюнкция (соответственно, дизъюнкция) литер. Конъюнкт (дизъюнкт) называется совершенным, если он содержит все пропозициональные переменные рассматриваемой формулы. Определение.Конъюнктивной нормальной формой (сокращенно КНФ) называется дизъюнкт или конъюнкция дизъюнктов. Дизъюнктивной нормальной формой (сокращенно ДНФ) называется конъюнкт или дизъюнкция конъюнктов. При этом КНФ (соответственно, ДНФ) называется совершенной, если совершенны все ее дизъюнкты (соответственно, конъюнкты). Теорема 1. Любая формула равносильна некоторой ДНФ и некоторой КНФ. Теорема 2. Любая выполнимая формула Такая формула определяется однозначно (с точностью до порядка членов конъюнкций и дизъюнкций) и называется совершенной дизъюнктивной нормальной формой (сокращенно СДНФ) формулы Теорема 3. Любая опровержимая формула Такая формула определяется однозначно (с точностью до порядка членов конъюнкций и дизъюнкций) и называется совершенной конъюнктивной нормальной формой (сокращенно СКНФ) формулы Логическое следование формул. Определение. Формула Символическое обозначение Формулы Определение. Множество формул Лемма (Транзитивность логического следования). Если
Лемма (Критерии логического следования). Условие a) b) c) В частности, Основные правила логического следования: 1) правило отделения (или правило модус поненс – от латинского modus ponens)
2) правило контрапозиции
3) правило цепного заключения
4) правило перестановки посылок
Метод резолюций в алгебре высказываний Определение. Пусть для некоторой переменной X дизъюнкты Резольвента дизъюнктов Определение. Резолютивным выводом формулы F из множества дизъюнктов 1) Fn=F; 2) каждая из формул Fi (i=1,…,n) либо принадлежит множеству S, либо является резольвентой Теорема. Множество дизъюнктов Так как по критерию логического следования соотношение
равносильно условию
то справедлив следующий результат. Следствие (Проверка логического следования формул). Пусть для формул Тогда логическое следование 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
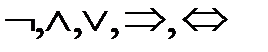 .
.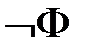 ),
), 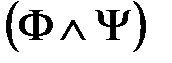 ,
,  ,
, 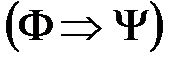 ,
, 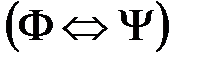 .
.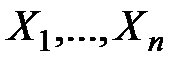 , то записывают
, то записывают  .
.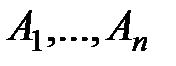 , то получится некоторое сложное высказывание
, то получится некоторое сложное высказывание  .
.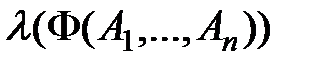 определяется истинностными значениями исходных высказываний
определяется истинностными значениями исходных высказываний 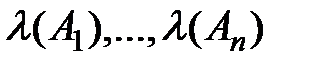 согласно таблицам истинностных значений логических операций
согласно таблицам истинностных значений логических операций 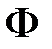 называется:
называется: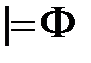 , если ее истинностная функция тождественно равна 1;
, если ее истинностная функция тождественно равна 1;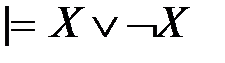 – закон исключенного третьего,
– закон исключенного третьего, – закон двойного отрицания,
– закон двойного отрицания, – закон противоречия,
– закон противоречия,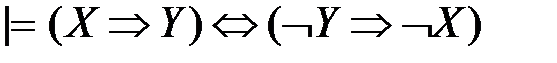 – закон контрапозиции.
– закон контрапозиции.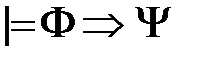 , то
, то 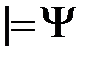 .
. , то для любых формул
, то для любых формул  тавтологией является формула
тавтологией является формула 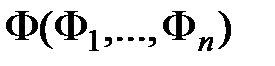 .
. называются логически эквивалентными (или просто равносильными), если
называются логически эквивалентными (или просто равносильными), если  .
.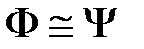 , или просто
, или просто  .
.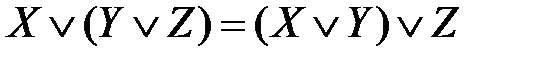 ,
,  – свойства ассоциативности дизъюнкции и конъюнкции;
– свойства ассоциативности дизъюнкции и конъюнкции; ,
,  – свойства коммутативности дизъюнкции и конъюнкции;
– свойства коммутативности дизъюнкции и конъюнкции;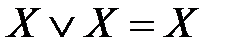 ,
, 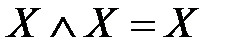 – свойства идемпотентности дизъюнкции и конъюнкции;
– свойства идемпотентности дизъюнкции и конъюнкции;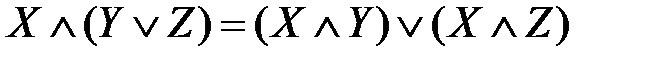 ,
,  – законы дистрибутивности конъюнкции относительно дизъюнкции и дизъюнкции относительно конъюнкции;
– законы дистрибутивности конъюнкции относительно дизъюнкции и дизъюнкции относительно конъюнкции; ,
, 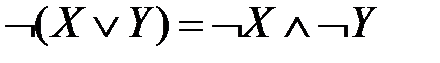 – законы де Моргана;
– законы де Моргана;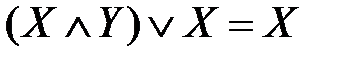 ,
, 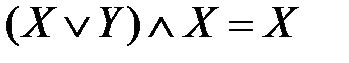 – законы поглощения;
– законы поглощения; – закон двойного отрицания;
– закон двойного отрицания; ,
, 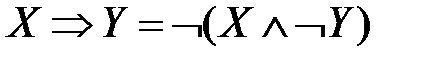 – взаимосвязь импликации с дизъюнкцией и конъюнкцией;
– взаимосвязь импликации с дизъюнкцией и конъюнкцией;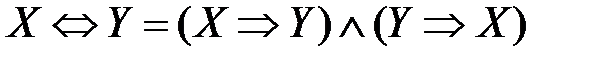 ,
, 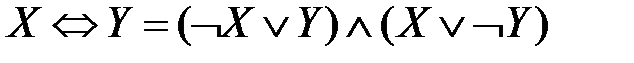 – взаимосвязь эквивалентности с импликацией, дизъюнкцией и конъюнкцией.
– взаимосвязь эквивалентности с импликацией, дизъюнкцией и конъюнкцией. равносильны, то для любой формулы
равносильны, то для любой формулы  ,содержащей переменную X,выполняется равенство:
,содержащей переменную X,выполняется равенство:  =
= 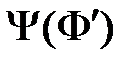 .
.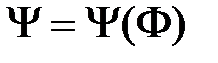 некоторой ее подформулы
некоторой ее подформулы 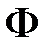 на равносильную ей формулу
на равносильную ей формулу  получается формула
получается формула 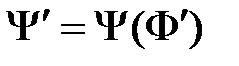 , равносильная исходной формуле
, равносильная исходной формуле 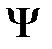 .
. является отношением эквивалентности на множестве всех формул FАВ, которое разбивает это множество на классы эквивалентности
является отношением эквивалентности на множестве всех формул FАВ, которое разбивает это множество на классы эквивалентности  , определяемые формулами
, определяемые формулами 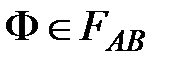 .
. .
.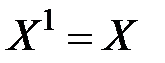 ,
,  .
.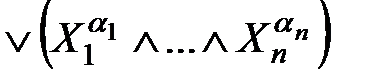 , где дизъюнкция берется по всем упорядоченным наборам
, где дизъюнкция берется по всем упорядоченным наборам 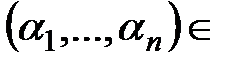 {0,1}n, удовлетворяющим условию
{0,1}n, удовлетворяющим условию 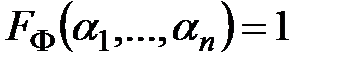 .
.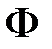 .
. , где конъюнкция берется по всем упорядоченным наборам
, где конъюнкция берется по всем упорядоченным наборам 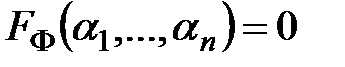 .
. .
.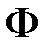 называется логическим следствием формул
называется логическим следствием формул 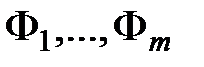 , если при любой подстановке в эти формулы вместо их переменных
, если при любой подстановке в эти формулы вместо их переменных 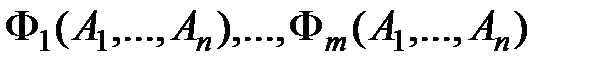 следует истинность высказывания
следует истинность высказывания 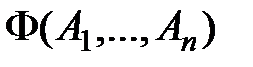 .
. - называется логическим следованием.
- называется логическим следованием.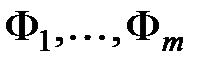 называется противоречивым, если из него логически следует любая (в том числе и тождественно ложная) формула
называется противоречивым, если из него логически следует любая (в том числе и тождественно ложная) формула 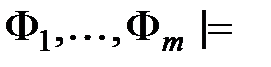 .
.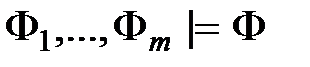 и для любого значения
и для любого значения 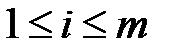 выполняется
выполняется  , то
, то 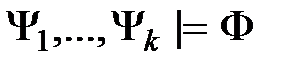 .
. равносильно каждому из следующих условий:
равносильно каждому из следующих условий: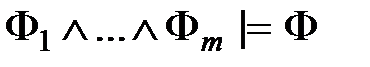 ,
, ,
, .
.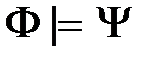 равносильно
равносильно 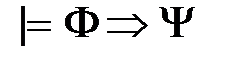 . Отсюда также следует, что
. Отсюда также следует, что 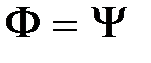 равносильно тому, что
равносильно тому, что  .
.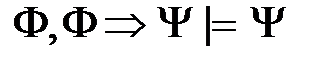 ;
;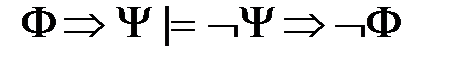 ;
;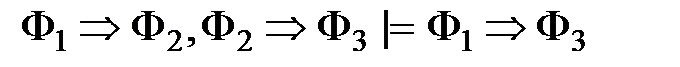 ;
; .
. представимы в виде
представимы в виде 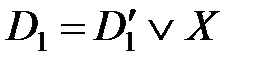 ,
, 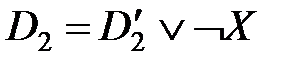 . Тогда дизъюнкт
. Тогда дизъюнкт  называется резольвентой дизъюнктов
называется резольвентой дизъюнктов 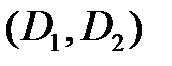 .
.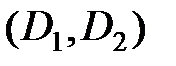 . По определению Res
. По определению Res 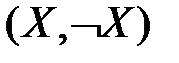 =0.
=0. называется такая последовательность формул
называется такая последовательность формул 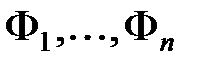 , что:
, что: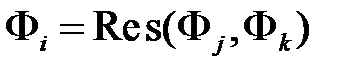 предыдущих формул Fj, Fk при некоторых 1£j,k£i.
предыдущих формул Fj, Fk при некоторых 1£j,k£i. 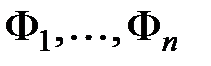 |=F
|=F |=,
|=, формула
формула  имеет КНФ
имеет КНФ 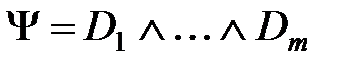 .
.